Classification Supervisée et Asymétrie ... des mots qui vont bien ensemble !

L’apprentissage à partir de données dont la distribution des modalités de la classe est très éloignée de la distribution uniforme, est une situation relativement fréquente dans certaines industries. Dans des situations comme le diagnostic des maladies, la gestion des défaillances des trains, la détection de fraudes bancaires ou le churn, le déséquilibre des jeux de données est la norme et pas l’exception. Dans ces cas, l’utilisation des méthodes d’arbres standard pour prédire l’étiquette d’un nouvel exemple n’est pas pertinente puisque les arbres optimisent le taux d’erreur globale, ce qui implique que la distribution des classes dans la feuille dépend de la classe la plus fréquente.    

Considérons que nous voulons détecter la fraude avec un jeu de données où 99% des cas appartiennent à la classe majoritaire et 1% appartiennent à la classe minoritaire (fraudeurs). Un approche traditionnelle d’un arbre de décision peut atteindre jusqu’à 99% de précision, ignorant seulement 1% des cas de classe minoritaire et ne pas tenir compte du fait que toutes les erreurs ont le même impact sur le business ; une classification erronée est plus coûteuse. Par conséquent, une approche traditionnelle peut aboutir à des résultats trompeurs car ils sont construits sur deux hypothèses : (1) minimiser le nombre d’erreurs, (2) le jeu de données d’apprentissage est un échantillon représentatif de la population.

Comment gérer le déséquilibre ?

Différentes méthodes que nous pouvons regrouper en deux catégories principales ont déjà été proposées pour traiter le déséquilibre des classes en apprentissage supervisé :

– Des stratégies d’échantillonnage visant à rééquilibrer les données. Ces méthodes pouvant par ailleurs être utilisées avec n’importe quelle méthode d’apprentissage supervisé.

– La prise en compte explicite de l’asymétrie des classes au sein même de l’algorithme généralement sous la forme de matrice de coûts (Cost Sensitive Learning) ou des objectifs précis spécifiés par l’utilisateur. Des approches ensemble permettent de rendre n’importe quel type d’algorithme sensible à l’asymétrie, notamment par des méthodes de boosting ou du bagging.

1. Stratégies d’échantillonnage

Un approche simple à mettre en œuvre pour redresser la distribution asymétrique de données est de supprimer de manière aléatoire des individus de la classe majoritaire ou d’augmenter les individus de la classe minoritaire.

Dans le premier cas nous parlons du sous-échantillonnage et le deuxième correspond à un sur-échantillonnage.  Les deux ont l’avantage d’être faciles à déployer mais ils portent aussi des inconvénients.

D’une part le sous-échantillonnage intègre le risque de supprimer des individus représentatifs pour l’apprentissage.  Pour éviter cet inconvénient, il existe plusieurs stratégies, à partir de différents critères comme le lien de Tomek, qui consiste à sélectionner des individus de la classe majoritaire qui sont moins sensibles au bruit et qui ne sont pas loin de leur voisinage.          

D’autre part le sur-échantillonnage peut entraîner des problèmes d’overfitting. Pour dépasser cet inconvénient la méthode Smote (Synthetic Minority Oversampling Technique) peut être utilisé. L’idée de SMOTE est d’augmenter le rappel pour la classe minoritaire en générant des individus synthétiques. Ces individus artificiels sont créés à partir d’un choix aléatoire (selon le taux de sur-échantillonnage voulu) d’un certain nombre de voisins plus proches qui appartient à la même classe. Pour entrer plus en détail, SMOTE calcule la différence entre le vecteur caractéristique (échantillon) considéré et son voisin le plus proche, après il multiplie cette différence par un nombre aléatoire compris entre 0 et 1 et il l’ajoute au vecteur caractéristique considéré. Ensuite les individus synthétiques sont disséminés aléatoirement le long de la ligne entre l’individu de la classe minoritaire et ses voisins sélectionnés. Ainsi, cette approche fait que la région de décision de la classe minoritaire soit plus grande et général.

2. Stratégies algorithmiques

Parmi les méthodes d’apprentissages supervisées, les arbres de décisions sont de plus en plus utilisés pour faire modèles de classification. Cependant, il faut adapter les arbres de décision à la présence d’asymétrie dans le jeu de données lors de deux étapes. Premièrement, pour choisir la meilleure variable et le meilleur point d’éclatement pour la création d’une nouvelle partition. Le deuxième aspect est la définition de règles d’assignation d’une classe à chaque feuille.

a. Critère de partitionnement 

Un des fondements des arbres de décision est l’utilisation de l’entropie comme mesure d’incertitude.  Dans les arbres de décision le processus de partitionnement se déroule par raffinement itératif de la partition grossière vers des partitions de plus en plus fines dont les éléments sont de faible entropie ou incertitude pour pouvoir induire de meilleurs modèles prédictifs.

Les critères classiques comme l’indice de Gini ou le critère de Shannon sont basés sur les hypothèses que la distribution des individus parmi les classes est uniforme et qu’ils sont également représentés. Cependant, dans la présence d’asymétrie ces critères peuvent engendrer des biais dans la phase de partitionnement des arbres de décision.      

Pour contrecarrer cet effet, il faut rendre asymétrique la mesure d’entropie en utilisant les trois approches suivantes : 

– Si la matrice de coût est connue nous pouvons introduire l’asymétrie des coûts de mauvaises classifications.

– Changer la distribution a priori des classes sous la forme d’un vecteur de probabilités.

Il y a des techniques comme le boosting qui permet d’adapter le taux d’erreur en fonction d’un coût d’erreur ou selon la probabilité de sa classe en affectant des poids différents aux individus du jeu d’apprentissage. Après chaque itération le poids sur les individus mal classés augmente et celui sur les individus classés diminue correctement. Les erreurs étant souvent concentrées sur les classes rares, on peut penser que le boosting permet d’améliorer l’apprentissage sur les jeux de données déséquilibrés en augmentant le poids des individus appartenant à la classe minoritaire.

Différentes variantes du boosting ont été proposées pour l’adapter spécifiquement au problème de déséquilibre (Figure 1). AdaCost assigne des poids plus élevées pour les erreurs sur la classe minoritaire. Avec RareBoost, si le nombre de vrais positifs est supérieur au nombre de faux positifs le poids des individus bien classés diminue, et si le nombre de vrais négatifs est supérieur à celui des faux négatifs, le poids des individus mal classés augmente.

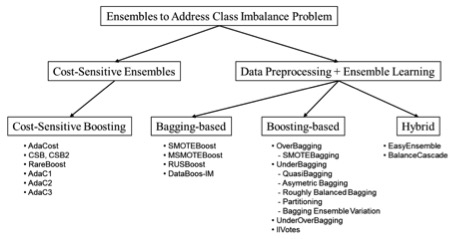
Figure 1. Ensemble méthodes pour gérer l’asymétrie

Source Galan et al (2012)

Il a aussi deux méthodes pour utiliser les forêts aléatoires sur les jeux de données déséquilibrées. La première, Balanced Random Forest (BRF), consiste à effectuer un bootstrap sur la classe minoritaire, puis à tirer le même nombre d’individus dans la classe majoritaire (avec remise). Leur deuxième approche est intitulée Weighted Random Forest (WBF) et consiste simplement à construire des arbres sensibles aux coûts (au niveau du critère de partitionnement avec une pondération de l’indice de Gini, et de l’affectation en modifiant le seuil).

– Utiliser des critères alternatifs aux Gini et Shannon comme l’entropie décentrée (Off Centered Entropy) et l’entropie asymétrique.

La figure 2 montre comment l’entropie décentrée et l’entropie asymétrique, à différence de l’entropie de Shannon, sont des entropies est qu’elles sont maximales lorsque la distribution est très éloignée de l’uniformité.

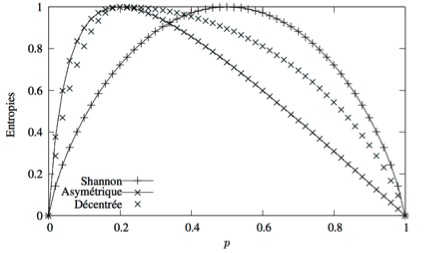
Figure 2. Entropies décentrée, asymétrique et de Shannon

Source : Lallich et al (2007)

b. Règles d’affectation    

La règle utilisée par la plupart des algorithmes d’induction d’arbres est la règle majoritaire : lorsque la feuille considérée est pure, il paraît évident que la feuille sera affectée à la seule classe représentée. Cependant, en situation d’asymétrie, lorsque les classes sont très déséquilibrées, la règle majoritaire n’est pas pertinente. Il faut utiliser des règles d’affectation comme les règles de seuils cohérentes avec les critères de partition que nous venons de présenter et qui permettent d’affecter la classe i à une feuille uniquement si la probabilité de classe dans la feuille dépasse la probabilité d’origine. 

En présence d’une variable d’intérêt très asymétrique, les prédictions des démarches usuelles de classification voient leur qualité dégradée. Cet article propose des solutions permettant d’améliorer la performance de votre modèle, ce qui peut mener à des gains significatifs en production : réduction du volume d’opérations de maintenance inutiles, meilleur total de fraude déjouée, etc. Chaque solution a ses avantages et inconvénients, il vous revient de tester selon le contexte laquelle de ces approches sera la plus performante !

Sources :

*M. Galar, A. Fernández, E. Barrenechea, H. Bustince, F. Herrera, A review on ensembles for class imbalance problem: bagging, boosting and hybrid based approaches, IEEE Transactions on Systems, Man, and Cybernetics – part C: Applications and Reviews 42 (4) (2012) 463–484

*S. Lallich, P. Lenca, B. Vaillant, Construction d’une entropie décentrée pour l’apprentissage supervisé, Université́ Lyon 2, France.