Comment modéliser la valeur de vie client dans un cadre contractuel ?

Introduction
Qu’est-ce que la valeur de vie client ?
La valeur de vie client mesure le profit moyen que peut faire une entreprise pour un client donné sur toute la durée de sa relation avec celui-ci.
Elle a pour objectif de déterminer a priori la valeur anticipée d’un client ou prospect à partir de son profil. Elle est très répandue dans les domaines des services (banque, assurances, télécom) ou dans le e-commerce, ainsi que dans tous les domaines où la fidélité client est importante.
Contrairement à ce qu’on pourrait penser, la valeur de vie n’est pas directement observable et doit être calculée à partir d’un modèle mathématique. Différents modèles existent pour les cadres contractuels/non contractuels et permettent d’utiliser l’historique de données du comportement des clients pour retranscrire certains phénomènes comme la fidélité client. Ces modèles prédisent la valeur de vie client (résiduelle pour des anciens clients) en fonction de caractéristiques comme leur ancienneté, âge, etc.
Une bonne estimation de la valeur de vie client est un enjeu important dans la stratégie marketing de l’entreprise : notamment d’augmenter la productivité́ des investissements marketing.
Elle permet ainsi :
-
d’optimiser les investissements en concentrant les efforts de la marque sur les clients les plus rentables.
-
de déterminer la limite haute d’un coût d’acquisition client.
-
de développer la rentabilité́ d’un client en participant à l’accroissement de son taux d’équipement.
-
d’estimer le risque d’impayés, de résiliation d’abonnement, de passage à la concurrence.
Elle fait donc partie des métriques les plus importantes pour améliorer la connaissance client.
Cadre de modélisation de la valeur de vie client
Dans la littérature, on classe souvent les cas de modélisation de la durée de vie client à l’aide du quadrant suivant[1], qui dépendent de deux questionnements :
-
la relation avec le client est-elle contractuelle ou non ?
-
les transactions se font-elle de façon continue ou discrète ?

Définition mathématique
La valeur de vie client, notée CLV (Customer Lifetime Value), correspond à la somme des profits attendus en moyenne par une entreprise sur toute la durée de la relation avec un client.
Il existe de nombreuses définitions mais la définition la plus répandue est celle utilisée par Fader et Hardie[3] :

où :
-
S(t) est la probabilité d’être actif jusqu’au temps t
-
Mt sont les revenus nets à l’instant t
-
d est le taux d’actualisation
Le taux d’actualisation permet de ramener sur une même base tous les flux financiers non directement comparables, car ils se produisent à des dates différentes.
La valeur de vie client repose donc sur deux estimations :
-
l’évolution théorique des consommations du client
-
la durée de vie du client
CLV dans un cadre contractuel
Dans la littérature sur la valeur de vie client, la durée de vie du client est souvent estimée à travers des modèles paramétriques. Le modèle Bêta-Géométrique présenté par Hardie et Fader[4] est un modèle utilisé pour déterminer la durée de vie client dans un cadre contractuel, à temps discret. On entend précisément par “temps discret” le fait que les transactions du client ne peuvent se faire qu’à des points fixés dans le temps (annuellement, ou mensuellement, c’est le cas par exemple pour les assurances où les cotisations sont annuelles ou bien mensuelles). Le cadre est “contractuel” si le moment où le client devient inactif est observé (par exemple, lorsqu’un client ne renouvelle pas son contrat).
Le modèle repose sur trois hypothèses :
-
chaque client a une probabilité θ de démissionner
-
La probabilité que le client soit actif jusqu’au temps t suit une loi géométrique, ie S(t|θ) = (1-θ)t
-
La probabilité de démissionner θsuit une distribution bêta de paramètre a et b
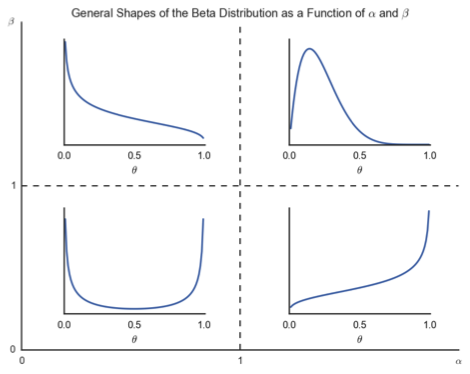
La loi bêta a été choisie ici car elle représente bien l’hétérogénéité des clients. En effet, selon les valeurs de ces paramètres α et β, la distribution bêta a des formes très différentes qui permettent de modéliser en autre des effets de fidélisation de la clientèle, comme expliqué plus loin.
Dans l’article scientifique, Fader et Hardie montrent comment estimer le modèle bêta-géométrique sous Excel. Je reprends ici les données utilisées dans l’article pour implémenter ce modèle sous R. Ci-dessous, « active » correspond à la proportion de clients toujours actifs au cours du temps et « lost » correspond à la proportion de clients qui sont partis.

Calcul de la Vraisemblance
Supposons que nous ayons 7 années d’observations. Soient n1 le nombre de clients qui démissionnent à la première période, n2 le nombre de clients qui démissionnent à la deuxième période, . . . , n7 le nombre de clients qui démissionnent à la septième période et n le nombre initial de clients au début de la période d’observation. On a donc n − clients toujours actifs à la fin de la septième période. On rappelle que α et β sont les estimateurs de la loi Béta de notre modèle Béta-Géométrique. On note P (T = t|α, β) la probabilité́ d’avoir une durée de vie de t périodes et S(t) la probabilité́ d’être encore actif à la fin de la période t.
La log-vraisemblance s’écrit :
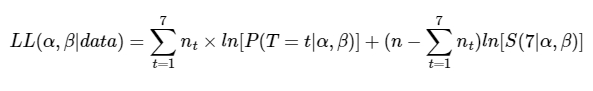
Les paramètres α et β sont alors les estimateurs du maximum de vraisemblance.
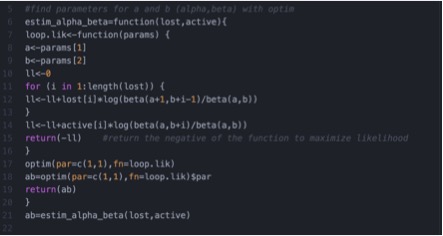
Représentation des résultats
On peut alors comparer l’évolution du taux de rétention par rapport l’estimation paramétrique de notre modèle :
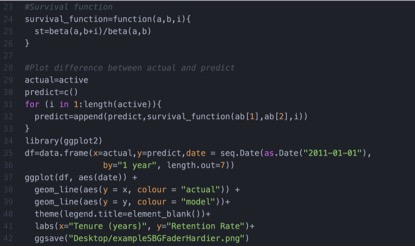
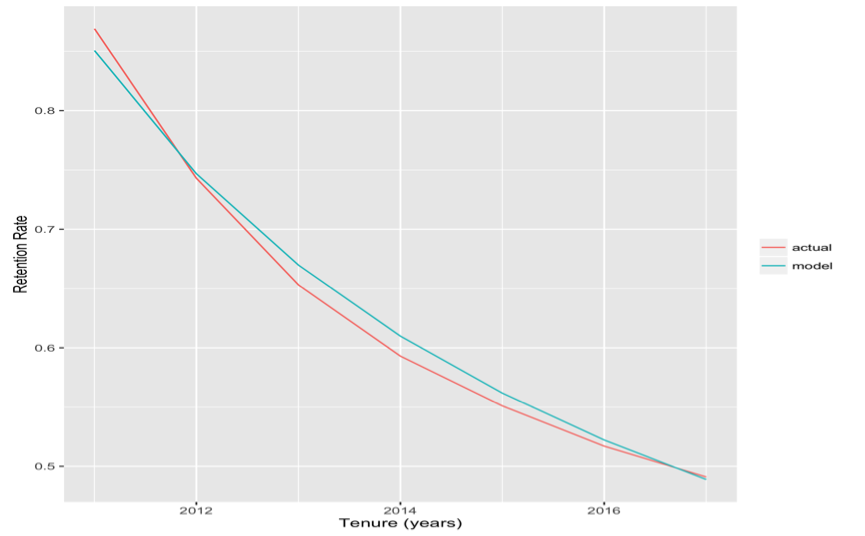
Limitations du modèle
L’estimation du modèle repose sur la segmentation des clients en cohortes. Une cohorte est définie selon l’année d’acquisition et possiblement d’autres caractéristiques du client. Lorsque l’on fait face à des cas multiples de cohortes, on observe différentes tailles de segments clients. Ce qui pose un problème sur la significativité des populations qu’on observe. Il y a plusieurs approches pour palier ce problème :
1. On peut choisir de regrouper ensemble des cohortes et d’estimer un unique couple de paramètres α et β.
2. On peut estimer des couples de paramètres pour chaque cohorte et calculer des intervalles de confiance. (Pour une estimation du modèle par une approche bayésienne, voir le très bon article de Daniel Weitzenfeld à ce sujet[5])
3. Enfin, on peut utiliser une version “beta-logistique” du modèle avec des variables discrétisées en fonction de la cohorte.
Exemple de cas d’usage
Espérance résiduelle de la CLV (DERT)
Après avoir estimé notre modèle, on peut calculer le nombre de renouvellements futurs espérés par segment de clients, appelée l’espérance résiduelle de la CLV (DERT, Discounted Expected Residual Transactions).
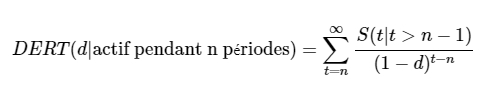
On multiplie le DERT par le profit d’un client sur une période, on suppose alors que le profit est le même sur toutes les périodes (ie m(t) = m) et on obtient la valeur de vie du client d’un segment espéré́. Cette méthode est applicable pour les entreprises dont les revenus par client sont constants dans le temps, ce qui est possible pour les assurances où le revenu est composé des cotisations fixes duquel on soustrait un terme de risque moyen.
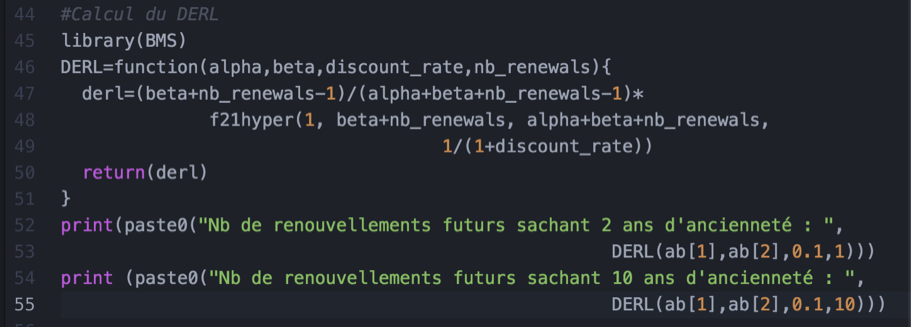
Ainsi, dans nos données issues de l’article de Fader et Hardie, on estime qu’un client avec déjà 10 ans d’ancienneté est susceptible de rester encore 7 ans, alors qu’un client qui a 2 ans d’ancienneté est susceptible de rester 5 ans. Ce qui est représentatif de la fidélité client.
[2] https://github.com/CamDavidsonPilon/lifetimes
[3] Peter S. Fader, Bruce G. S. Hardie. What’s Wrong With This CLV Formula ? December 2014.
[4] Peter S. Fader, Bruce G. S. Hardie. How to Project Customer Retention. 2007

