Les exemples adverses ne sont pas des erreurs, ce sont des features !

✍ Michaël Sok / Temps de lecture : 12 minutes
Sous ce titre racoleur se cache un article particulièrement intéressant rédigé par Ilyas et al. pour l’édition 2019 de la fameuse conférence scientifique NeurIPS [1] (en anglais Adversarial Examples are not Bugs, They are Features [2]). En effet, comme son nom l’indique, cet article se focalise sur le domaine des attaques adverses et pose le postulat que les exemples adverses ne sont pas dépendants d’un modèle en particulier, mais plutôt des features qu’il apprend et qui sont intrinsèques au jeu de données.
Comment définissons-nous les features ?
Avant d’entrer dans le vif du sujet, redéfinissons ce que nous appellerons par la suite feature. Une feature se définit comme étant une caractéristique intrinsèque du jeu de données qu’un modèle extrait et sur lequel il se base pour effectuer sa prédiction. Par exemple, pour un humain cela pourrait se caractériser par la profondeur d’une image, le contour de l’objet etc. Une définition plus formelle d’une feature est une fonction de correspondance f entre l’espace des données en entrée X et l’espace réel \mathbb{R}.
f : X \rightarrow \mathbb{R}
Dans le cas particulier d’un réseau de neurones, les features sont les données de sortie de l’avant-dernière couche de ce réseau. Ainsi la sortie de l’intégralité du réseau serait équivalente à celle d’une régression sur ces features :
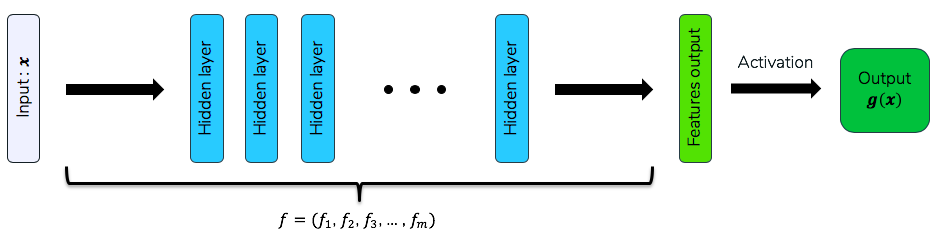
Features obtenues par un réseau de neurones quelconque
Ici, nous avons donc le réseau de neurones g qui peut se définir formellement de la manière suivante :
g(x) = a\left(w_0 + \sum_{i=1}^{m}w_i f_i(x)\right)
avec a la fonction d’activation de la couche finale, f_i les différentes features apprises par g et w_i les poids de la régression utilisés dans la dernière couche de prédiction.
Il faut donc bien distinguer les features de cet article qui se définissent comme les caractéristiques intrinsèques d’un jeu de données et qui sont pertinentes pour la tâche de prédiction et la définition habituelle du mot “features” qui est souvent équivalente au sens de variables explicatives.
Que recherchons nous dans une feature ?
Il est évident que nous cherchons à ce que les features apprises par notre modèle soit causales, c’est à dire qu’une variation de la dite feature cause une variation dans la variable cible. Il est cependant très compliqué de trouver de telles relations et surtout de l’exprimer mathématiquement. Une alternative est d’exprimer la corrélation entre deux variables. L’indice le plus connu pour cela est le coefficient de corrélation de Pearson :
\rho_{X, Y} = \frac{\text{cov}\left(X, Y\right)}{V(X)V(Y)} = \frac{\mathbb{E}\left[\left(X-\mu_X\right)\left(Y - \mu_Y\right)\right]}{V(X)V(Y)}
qui étudie l’existence d’une quelconque relation linéaire entre deux variables X et Y. Cet indice étant défini, les auteurs de l’article se sont ensuite placés dans un cadre de classification binaire, avec y \in \{-1, 1\} afin de faciliter les calculs.
Sous hypothèse faible de variables centrées réduites, nous pouvons donc écrire la corrélation de la manière suivante :
\rho_{X, Y} = \mathbb{E}\left[XY\right]
Et c’est de cette définition que nous allons partir pour écrire les caractéristiques pertinentes pour une feature :
- Une feature est pertinente pour accomplir la tâche de prédiction si elle est suffisamment corrélée avec la variable cible. Nous dirons ainsi qu’une feature
f_iest\rho– utile si sa corrélation est supérieure à\rho:\mathbb{E}\left[f_i(x)y\right] > \rho. - Si une feature
f_ireste pertinente pour accomplir la tâche de prédiction, même lorsque les données d’entrées sont perturbées, alors nous dirons qu’elle est\gamma– robustement utile. Cela se traduit par une corrélation qui reste supérieure à\gammamême lors de perturbations sur les données d’entrée selon une stratégie d’attaque\Delta:\mathbb{E}\left[\inf_{\delta \in \Delta(w)}f_i(x+\delta)y\right]>\gamma.
De par ces définitions, il devient intuitif de penser qu’un modèle robuste à une certaine stratégie d’attaque semble apprendre des features robustement-utiles tandis qu’un modèle classique apprendrait simplement des features utiles qui lui semble hautement prédictives sans a priori sur une certaine stratégie d’attaque.
Que se passe-t-il si nous exacerbons les features robustement utiles ?
Création d’un dataset « robuste »
Il existe de nombreux exemples démontrant la “faiblesse” des réseaux de neurones face à des attaques adverses comme par exemple la création d’un patch qui transformerait n’importe quelle classification d’un modèle en grille pain [3].
Si nous suivons les définitions précédentes, ce ne serait finalement dû qu’à l’existence de features hautement prédictives mais finalement peu robustes face à des attaque adverses. Pour vérifier ce postulat, les auteurs de l’article [2] ont essayé de créer un jeu de données permettant d’apprendre des features robustement utiles. Les auteurs se sont servis d’un modèle entraîné par entraînement adverse, dit robuste, et ont exacerbé les features apprises par celui-ci, à la manière d’une méthode de transfert de style.
Plus concrètement, Ilyas et al. ont essayé de créer des observations qui ont la même représentation par le modèle robuste que les données d’origine. La méthode consiste en une descente de gradient initialisée par une observation choisie de manière aléatoire. Durant chaque étape de la descente de gradient, les observations sont projetées dans l’espace possible des images. C’est avec ce processus de sélection aléatoire que les auteurs espèrent ne retenir que les features pertinentes pour le modèle robuste sans s’encombrer des potentielles features utiles mais non robustes.
Le pseudo-algorithme utilisé dans l’article pour obtenir un jeu de données exacerbant les features apprises est le suivant :

Pseudo-Algorithme pour créer un jeu de données robuste D_R
L’objectif est donc bien de minimiser la représentation d’un modèle robuste entre deux observations choisies de manière indépendante dans le jeu de données.
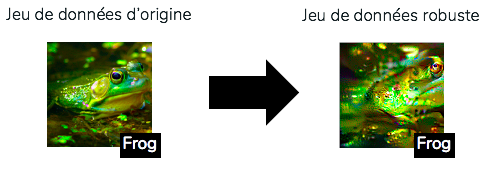
Exemple de transformation du jeu de données en jeu de données robuste
Les résultats après entraînement sur le dataset « robuste »
En se servant de ce jeu de données robuste, nous pouvons entraîner un modèle de manière classique et s’intéresser aux résultats. Nous observons alors un modèle à la fois bon sur un jeu de données test suivant une distribution habituelle et qui obtient également des résultats non triviaux sur un jeu de données perturbées par une stratégie d’attaque !
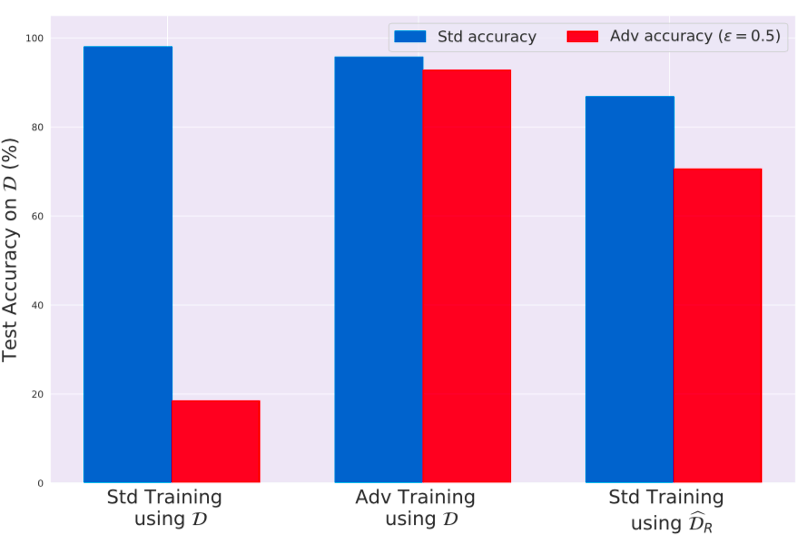
Résultats sur Restricted-ImageNet avec un jeu de données de test classique et un jeu de données perturbé par attaque adverse. À gauche avec un modèle entraîné sur le jeu de données d’entraînement d’origine, au milieu avec un modèle entraîné par entraînement adverse sur le jeu de données d’entraînement d’origine et à droite avec un modèle entraîné sur le jeu de données constitué par reconstitution des features robustes
Cela nous apprend que si nous retirons du jeu de données toutes les features utiles mais non robustes (les features ignorées par le modèle robuste), alors un modèle entraîné par méthode standarde sur ce jeu de données ignore aussi ces features. Il est donc peu affecté face à la stratégie d’attaque utilisée pour entraîner le modèle robuste.
Ce jeu de données est cependant forcément conditionné par l’existence de ce fameux modèle “robuste”. En effet le modèle robuste pré-traite les données de manière à ne laisser en place que les features robustes comme pertinentes.
Un changement de paradigme
Cela laisse donc bien supposer qu’un modèle classique apprend des features qui pour lui sont hautement prédictives, mais qui ne sont pas forcément robustes. Mais qu’est-ce que cela nous apporte ? Nous utilisons souvent le critère de “faiblesse” d’un modèle face aux attaques adverse comme une preuve d’absence de robustesse. Pourtant, le problème pourrait ne pas provenir pas de là.
D’un point de vue humain, nous avons des attaques sur des images qui ne changent sensiblement pas notre perception de l’image, mais qui pourtant affectent la prédiction d’un modèle. Mais que se passe t-il lorsque nous changeons l’orientation du problème ? Et si nous créons des attaques qui justement changent radicalement la prédiction humaine de l’image ? Par exemple nous pourrions avoir une image évidente d’un chien, d’après un humain, classifiée comme un chat par le modèle. Ce ne serait finalement que la création d’attaques adverses sur la prédiction humaine du point de vue du modèle. Ainsi là où les attaques sont habituellement transparentes pour un humain, elles le sont ici pour le modèle.
Que se passe-t-il si nous attaquons le modèle “humain” ?
C’est ce qu’Ilyas et al. ont tenté d’étudier en créant un jeu de données qu’un humain qualifierait de mal labellisé mais dont un modèle arriverait à extraire des features pertinentes. Comme évoqué précédemment, la méthode pour créer ce jeu de données consiste simplement à ajouter une perturbation (de norme majorée par une petite constante \epsilon) mais qui maximise la probabilité d’une autre classe de prédiction (par exemple nous trouvons la perturbation maximale pour classer un chien en chat, d’après un modèle).
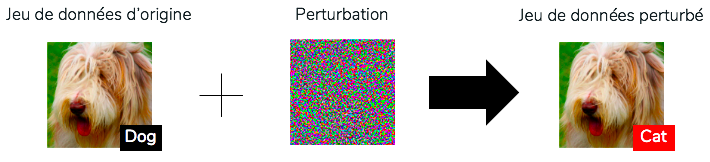
Exemple de transformation du jeu de données en jeu de données perturbé
Et si maintenant nous regardons les résultats d’un modèle qui s’entraîne sur le jeu de données perturbé, nous remarquons une chose particulièrement intéressante : le modèle arrive tout de même à bien prédire sur le jeu de données de test d’origine ! Cela signifie que le modèle a réussi à extraire des caractéristiques pertinentes pour pouvoir prédire sur la distribution finale, bien que les caractéristiques pertinentes observées par un humain soient absentes de l’image (puisque les labels ont tous été modifiés lors de la création de ce jeu de données). Si nous nous intéressons maintenant aux résultats sur le jeu de données de test d’origine mais perturbé par des attaques adverses, les performances du modèle chute, comme cela aurait été le cas sur un modèle entraîné sur les données d’origine. Ceci est alors bien en accord avec l’hypothèse que le modèle n’a fait qu’apprendre des features utiles mais non robustes !
Conclusion
Les résultats de cet article de recherche ont permis de montrer plusieurs choses. Un dataset possède deux types de features pertinentes pour une tâche de prédiction, une qui est simplement prédictive, tandis que l’autre est robuste à des perturbations dans le domaine d’entrée. Un modèle robuste semble bien apprendre les features robustes, ce qui explique sa faible sensibilité à des stratégie d’attaque, tandis qu’un modèle classique apprend des features utiles, à savoir hautement prédictives, mais non robustes.
Ces features utiles mais non robustes sont suffisantes pour obtenir de bons résultats sur un jeu de données réaliste, mais souffre effectivement d’une sensibilité à des attaques adverses. Toutefois il est irréaliste de penser qu’un modèle apprendrait des features robustes plutôt que simplement utiles. Après tout, cette notion de robustesse est spécifique aux humains et de ce que nous qualifions de « robuste ».
Ainsi, un entraînement robuste consisterait en une tentative de diminuer la valeur prédictive des features non robustes pour inciter un modèle à ne pas s’en servir. Ce résultat est d’autant plus important qu’il agit sur notre interprétation des modèles à travers les méthodes d’intelligibilité. En effet puisque le modèle repose sur des features qui ne sont pas robustes à des attaques transparentes pour les humains (c’est à dire ayant peu d’effet sur eux), une méthode d’intelligibilité n’a que deux choix pour justifier ces features :
- les souligner et avoir une interprétation ayant peu de sens pour un humain;
- les occulter mais avoir une explication du modèle trompeuse.
Finalement, si nous souhaitons avoir des méthodes d’intelligibilité qui aient à la fois du sens pour les humains, tout en étant fidèles au modèle, il faut agir directement au moment d’entraîner le modèle en introduisant des a priori humains sur les features à prioriser et qui ont du sens pour un humain !
✍Article écrit par Michaël Sok
Références
[1] Thirty-third Conference on Neural Information Processing Systems
[3] Tom B. Brown, Dandelion Mané, Aurko Roy, Martín Abadi, and Justin Gilmer. Adversarial patch, 2017.

