Quant Blog Le blog des Experts Data & IA

Uncategorized

27/03/2015

Initiation au Machine Learning

Temps de lecture : 7 minutes

Dans le cadre du master Urbantics de l’EIVP, Quantmetry a animé un TP de Data Science sur une thématique Smart Cities le vendredi 30 janvier 2015. En accord avec un acteur du secteur de la mobilité, nous disposions des données d’entrées, de sorties et de péages d’un parking géré par ce dernier. L’objectif était de construire un modèle simple de prédiction du taux d’occupation du parking à une heure donnée. Un document en annexe du TP donnait quelques explications sur la notion de modèle en machine learning, ainsi que sur les concepts de base associés. Nous le reproduisons sous forme d’article de Blog pour les amateurs intéressés par le machine learning!

Soit

un ensemble d’exemples, où i représente le numéro de l’exemple, x_i une variable explicative et y_i la variable à prédire ou variable cible. Chaque exemple correspond à un point dans un espace des variables, ici un plan. Si l’on dispose de plusieurs variables explicatives x¹, x² etc., alors la dimension de l’espace des variables augmente. Un modèle est la donnée d’une fonction f qui associe à chaque vecteur x de l’espace des variables explicatives une valeur y de la cible.

Nous passerons en revue dans cet article trois modèles : la régression linéaire, les arbres de décision et les forêts aléatoires, ainsi que les concepts de base associés à la mesure de leur performance.

LA RÉGRESSION LINÉAIRE

La régression linéaire cherche à construire la droite

qui correspond « le mieux » à la distribution des points (x_i,y_i), « le mieux » étant une notion qui reste à définir. Ainsi, pour une nouvelle valeur x_m+1 on aura une prédiction

pour la variable cible. De manière plus générale, la régression linéaire fournit l’hyperplan qui correspond « le mieux » aux données (voir Fig. 1).

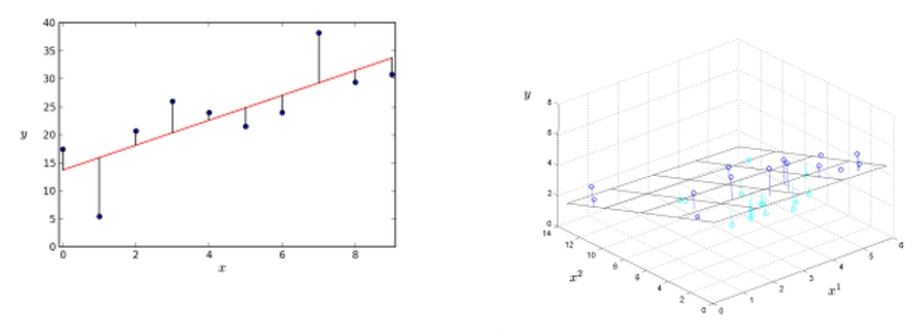
Figure 1 – Régression linéaire avec une et deux variables explicatives.

L’approche usuelle pour définir la qualité de la correspondance entre un modèle à paramètres fixés et les données est de définir une fonction de coût. Cette dernière permet de mesurer l’erreur des prédictions en les comparant aux valeurs prises par la cible. Pour la régression linéaire avec paramètres (a,b) , la fonction de coût correspond simplement à la somme des distances au carré entre la prédiction et la valeur réelle de la cible pour chaque exemple du jeu d’entraînement :

La recherche des paramètres optimaux du modèle correspond alors à une minimisation dans l’espace des paramètres de la fonction de coût, l’algorithme d’optimisation le plus connu étant la descente de gradient.

LES ARBRES DE DÉCISION

Un arbre de décision crée des compartiments dans l’espace de représentation des exemples par dichotomies successives selon chaque dimension de l’espace des variables explicatives.

Pour un nouvel exemple

d’un problème avec deux variables explicatives, l’arbre de décision renverra (voir Fig 2) :

La classe majoritaire du compartiment auquel il appartient s’il s’agit d’un problème de classification.

La moyenne des valeurs de la variable cible pour les exemples situés dans le même compartiment s’il s’agit d’un problème de régression.

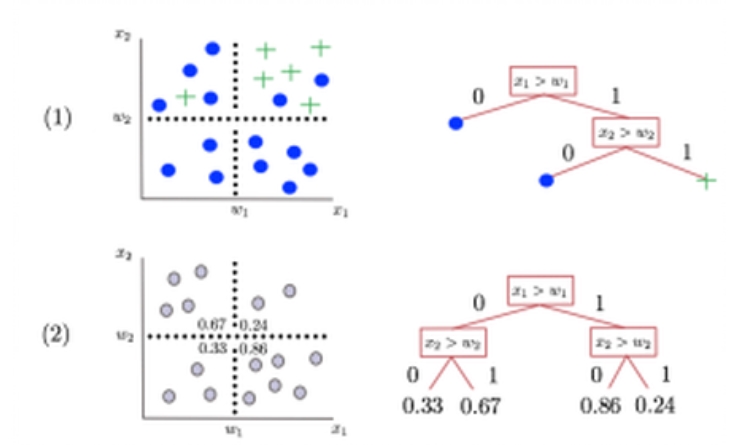
Figure 2 – (1) : Classification par vote dans un arbre de décision, (2) : Régression par moyenne dans un arbre de décision.

Cet algorithme nécessite de spécifier le nombre minimal de feuilles par compartiment servant à calculer la classe majoritaire ou une moyenne. L’algorithme minimisera son erreur sur le jeu d’entraînement pour un choix d’une feuille par compartiment : il fournira alors des prédictions exactes de la cible pour chaque valeur des variables explicatives sur les exemples d’entraînement. Cependant, il risque d’être très peu performant sur de nouveaux exemples car une partie des informations apprises correspond à des détails spécifiques aux exemples d’entraînement : c’est le phénomène de surapprentissage.

LES FORÊTS ALÉATOIRES

Une forêt aléatoire consiste en un ensemble fini d’arbres de décision α= a,b,c. Chaque arbre de décision est entraîné sur un sous-ensemble d’exemples et produira pour une nouvelle valeur une prédiction

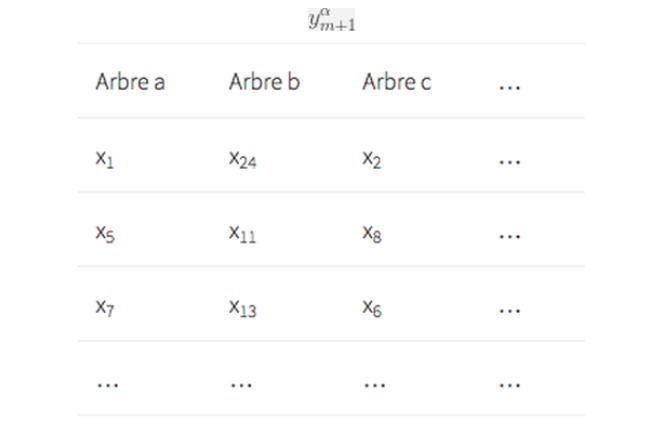
Figure 3 – Chaque arbre s’entraîne sur un sous-ensemble de l’ensemble initial d’exemples.

La magie s’opère en moyennant sur les prédictions

de tous les arbres: on obtient alors un arbre de décision aux prédictions plus précises, phénomène connu sous le nom de bootstrap aggregating ou de bagging.

LA RÉGULARISATION

Après l’étude de la régression linéaire, il est naturel de s’intéresser à des modèles polynomiaux :

Un des risques majeurs avec ce type de modèles est le surapprentissage. En effet, un polynôme de haut degré conjugué à des coefficients élevés en valeur absolue aura tendance à passer par tous les points du graphe de données, intégrant ainsi le bruit spécifique à l’échantillon d’entraînement, ce qui empêchera une bonne performance du modèle sur de nouveaux exemples (voir Fig 4).

Figure 4 – Augmenter le degré du polynôme sans borner la valeur absolue des coefficients peut conduire à une situation d’overfit.

Des techniques existent pour éviter ce problème de surapprentissage, la plus connue étant la régularisation.

Elle consiste en l’ajout d’un terme

à la fonction de coût (on ne régularise pas le terme α_0) :

Optimiser cette nouvelle fonction de coût impose des paramètres a_1,…,a_n petits, d’où un modèle avec moins de « collines »

(penser à

qui est moins « courbée » que 3x²) et donc une intégration moins importante du bruit associé à l’échantillon d’entraînement.

LA VALIDATION CROISÉE

L’étude des modèles polynomiaux illustre l’un des problèmes majeurs en machine learning, à savoir le compromis entre bonnes performances sur le jeu d’entraînement et sur de nouveaux exemples, i.e. entre la complexité du modèle et sa capacité prédictive. En effet, l’optimisation des paramètres d’un modèle (avec ou sans terme de régularisation dans la fonction de coût) améliore les prédictions du modèle pour le jeu d’exemples ayant servi à son entraînement, mais elle ne garantit en aucun cas une bonne capacité prédictive, i.e. de bonnes performances sur de nouveaux exemples.

Comment mesure-t-on la capacité prédictive d’un modèle? Une première approche intuitive serait de découper les exemples d’entraînement en deux sous-ensembles : un pour l’entraînement (à peu près 70% de l’ensemble original) et un autre (à peu près 30%) pour tester la capacité de généralisation du modèle. S’il s’avère que notre modèle se généralise mal, on sera tenté d’augmenter la valeur de λ pour diminuer le surapprentissage, ce qui conduira à un choix des paramètres du modèle avec une meilleure performance sur l’ensemble de test. Cependant, on introduit ainsi une corrélation entre le nouveau choix de paramètres du modèle et les données de l’ensemble de test, faussant ainsi notre estimation de la capacité de généralisation du modèle. Une solution à ce problème consiste en un découpage de l’ensemble d’entraînement en trois parties : un ensemble d’entraînement (60%), un ensemble dit de validation croisée (20%) pour lequel on optimisera le choix de paramètres du modèle, et enfin un ensemble de test (20%) qui permettra de tester sa capacité de généralisation.

LE COMPROMIS BIAIS-VARIANCE

Les techniques de régularisation et de validation croisée s’inscrivent dans une démarche plus générale d’étude des propriétés des paramètres du modèle en fonction du jeu d’entraînement. Quelles propriétés possède le modèle final choisi après régularisation et validation croisée?

Si l’on commence par un ensemble d’entraînement constitué d’un seul exemple que l’on agrandit à chaque itération, on pourra alors mesurer l’impact des nouvelles informations contenues dans chaque exemple en mesurant l’écart entre les paramètres des modèles successifs. Un écart élevé indiquera alors une grande sensibilité des paramètres aux nouvelles informations, et donc une notion d’instabilité du modèle.

De manière plus générale, on cherchera à mesurer la variance et le biais de la distribution des paramètres du modèle par changement du jeu d’entraînement : pour un nombre d’exemples suffisant, une variance forte signifiera que le modèle tend à capter des informations spécifiques aux exemples d’entraînement mais qui se généralisent mal, le plus souvent à cause d’une situation de surapprentissage, tandis qu’un biais fort signifiera que le modèle n’est pas assez complexe pour capter les spécificités du problème étudié, situation dite de sous-apprentissage. La recherche d’un compromis entre une diminution de la variance du modèle et une diminution du biais dans l’estimation des paramètres correspond en général à la solution optimale fournie par les techniques de régularisation et de validation croisée (voir Fig 5).

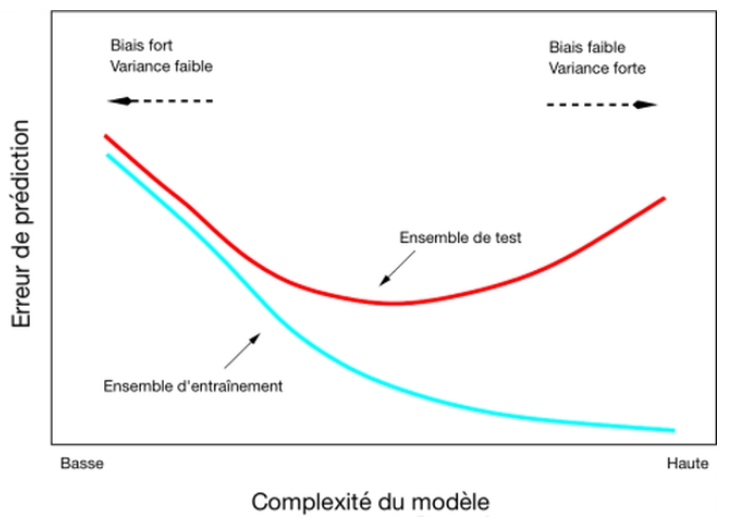
Figure 5 – Compromis biais-variance pour l’estimation des paramètres d’un modèle.

CONCLUSION

Les notions de modèle, de régularisation et de capacité de généralisation sont au coeur du machine learning, et nous n’avons fait qu’effleurer les liens entre ces trois notions dans cet article. Au coeur des notions d’apprentissage et de généralisation se situe la notion d’inférence bayésienne, qui fournit un nouvel éclairage sur la technique de régularisation. Plus de détails dans un article à venir!