Maintenance Prédictive et Séries Temporelles

Introduction

La maintenance prédictive représente aujourd’hui un enjeu prégnant pour les grands acteurs du monde industriel ou qui exploitent des infrastructures lourdes (énergie, transport, …).

Avec l’émergence de l’internet des objets, de plus en plus de machines sont équipées de capteurs remontant des informations pouvant être exploitées pour anticiper des défaillances aux conséquences opérationnelles coûteuses.

Cette problématique de maintenance prédictive n’est bien sûr pas nouvelle, on a toujours voulu anticiper les défaillances, mais avec la multiplicité croissante des capteurs équipant les machines c’est l’approche qui a changé. Dans le passé une démarche courante était de faire des analyses de survie en étudiant statistiquement les « temps avant défaillance » des machines et en prenant parfois également en compte quelques données statiques descriptives des machines. Cette approche conduisait à identifier des populations de machines à risque afin d’effectuer des opérations de maintenance préventive.

Or aujourd’hui avec les capteurs il est possible d’avoir une image dynamique beaucoup plus précise de l’état de chaque machine à tous les instants. Ces informations traitées avec du machine learning peuvent-elles contribuer à améliorer la maintenance ? C’est tout l’enjeu de notre article.

Nous voilà ramenés à cette catégorie de problèmes longtemps mise de côté par la communauté traditionnelle du machine learning : les séries temporelles.

Approche du problème

Considérons que les machines soient chacune représentées par un ensemble de séries temporelles et de dates de défaillances.

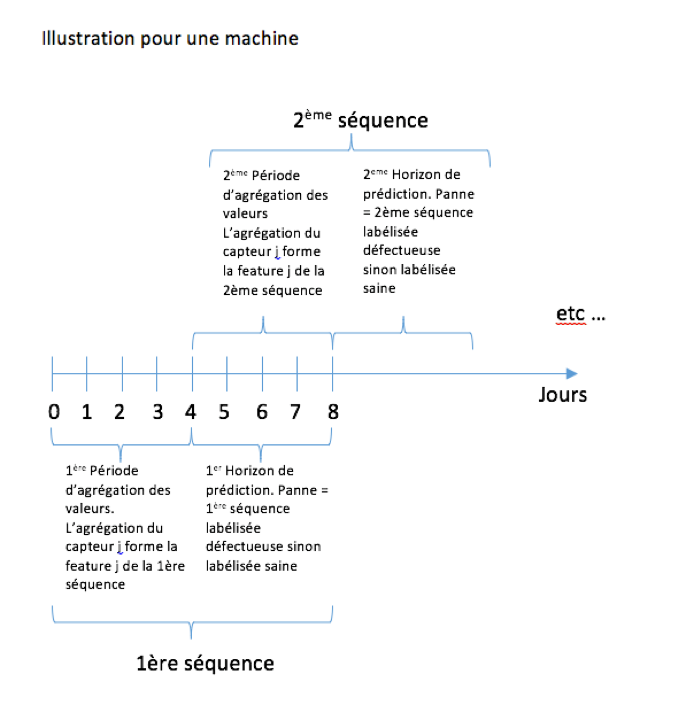
Méthode de construction de séquences.

Cette approche consiste à fabriquer des « séquences » pour chaque machine. Une séquence est composée des agrégations de chacune des valeurs des capteurs sur une période de temps fixée, appelée période d’agrégation. Si dans un certain horizon temporel après cette période d’agrégation une défaillance intervient, la séquence reçoit le label « panne », sinon elle reçoit le label « sain » (la cible). Chaque période d’agrégation est ensuite décalée pour déterminer la séquence suivante.

On effectue ce traitement pour chaque machine et on obtient alors un ensemble de séquences labéllisées « saines » ou « défectueuses ».

Ensuite les techniques d’apprentissage classiques telles que les fôrets aléatoires ou autre, peuvent être utilisées sur ce tableau de séquences pour prédire la cible.

Difficulté : déséquilibrage entre cibles « saines » et « défectueuses »

Dans ce type de problème un des aspects délicats est que les séquences labéllisées « défectueuses » sont beaucoup moins représentées que les séquences labéllisées « saines », il n’est pas rare de rencontrer moins de 0,1% de séquences défectueuses.

Cela se traduit par le fait qu’une courbe ROC qui semble refléter de bonnes performances cache en fait une performance bien moindre pour le métier. Cette performance réelle est mieux traduite par la courbe précision / recall, sur laquelle on voit tout de suite une qualité moindre.

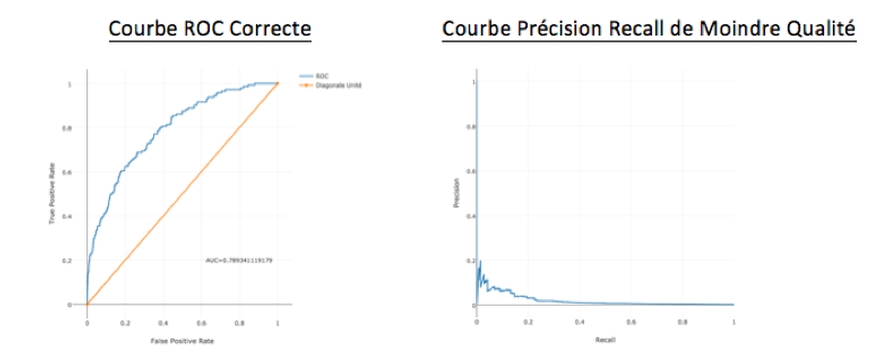
Cela s’explique par le fait que le False Positive Rate (FPR)* de la courbe ROC est calculé par rapport au nombre de séquences « saines » qui ici est extrêmement élevé.

Prenons un exemple, 100 000 séquences saines et 1000 séquences défectueuses, en zone optimale de score F1 le courbe ROC donne environ un FPR de 20% et un TPR de 60%. Ce qui signifie 20% x 100 000 = 20 000 fausses alertes et 60% x 1000 = 600 alertes correctes. 20 000 fausses alertes pour seulement 600 alertes correctes, cela donne une précision très faible (600/20600 = 3%).

Enrichissement de l’approche

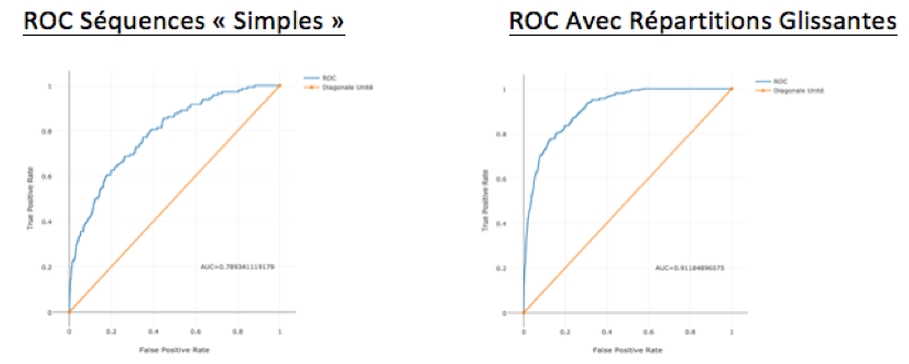
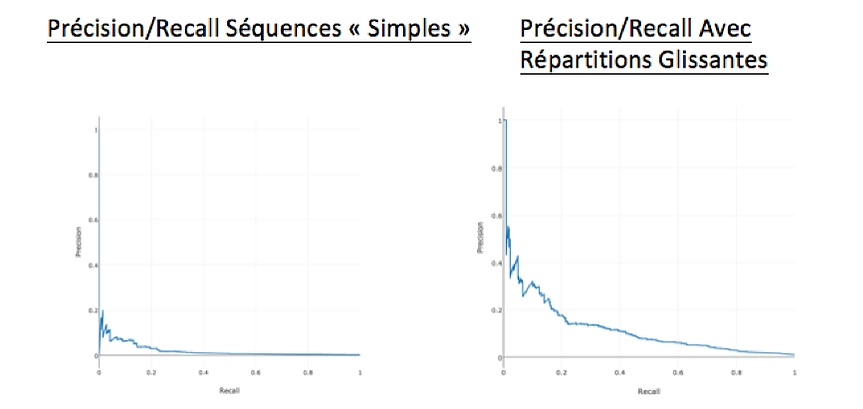
La limitation avec ce type d’approche est que l’on regroupe ensemble les séquences de toutes les machines, bien qu’elles puissent avoir chacune des comportements différents, ce qui a tendance à détériorer les performances de l’algorithme.

Une approche complémentaire consiste à ajouter une information sur la manière dont une machine évolue par rapport à elle-même. L’information suivie est alors le changement au cours du temps sur les signalisations d’un capteur d’une machine par rapport à lui-même, donc par rapport à son fonctionnement normal.

Une façon de faire ceci est de calculer les répartitions empiriques des valeurs de chaque capteur sur une période donnée en début de vie de la machine. Puis ensuite pour chaque nouvelle séquence, pour chaque capteur on calcule également ces mêmes répartitions empiriques et on crée une feature qui est la distance (choix de la distance en fonction des cas) entre la répartition de cette séquence courante et la répartition « de référence » calculée en début de vie de la machine.

Cette approche permet de faire ressortir les signaux faibles pouvant se déclarer dans les valeurs des capteurs avant que la défaillance ne soit « officiellement » découverte.

Nous avons constaté empiriquement une amélioration significative de la « prédictivité » de nos modèles, mesurée par un incrément de 10 points d’AUC et une multiplication de la precision/recall par 2 ou 3.

Conclusion

L’approche en séquences qui se pratique couramment pour ramener des problèmes de prédiction de séries temporelles à des problèmes de machine learning, se révèle parfois insuffisante dans les cas où les grandeurs à prédire sont fortement déséquilibrées comme en maintenance prédictive.

Nous avons alors constaté sur certains sujets l’intérêt de compléter cette démarche par l’ajout de nouvelles features traduisant l’évolution des signaux temporels par rapport à une période de référence fixée considérée comme « saine », et cela pour une même entité d’étude (machine par exemple).

* Les faux positifs sont les séquences prédites comme défaillantes alors qu’elles sont saines. A contrario les faux négatifs correspondent aux séquences prédites comme saines alors qu’elles sont défaillantes