Maintenance prédictive : un sujet brûlant

La thématique de maintenance prédictive constitue aujourd’hui un champ d’application du big data très dynamique. En tant que consultant, ces missions sont particulièrement intéressantes car elles nous immergent dans des univers métier passionnants ! La SNCF est particulièrement en pointe sur ces sujets et encourage de nombreux projets au sein de la direction du digital.
http://www.sncf.com/fr/presse/fil-info/internet-industriel-conf%C3%A9rence-de-presse/987456
http://www.sncf.com/ressources/pres_conf_presse_iot_v4_light.pdf
http://www.lefigaro.fr/flash-eco/2016/04/12/97002-20160412FILWWW00110-la-sncf-mise-sur-l-internet-industriel.php
La démarche exposée ci-dessous a été construite avec l’équipe projet Big Data Végétation dont les travaux ont été présentés lors de la conférence presse digital sncf.
L’enjeu du projet Big Data Végétation est d’identifier les zones du réseau propices aux incidents liés à la pousse de la végétation le long des voies comme les chutes d’arbres, les phénomènes de patinage, les collisions avec les animaux ayant trouvé refuge le long des voies et les incidents. L’idée est d’exploiter des sources d’information hétérogènes (incidents, météo, images de drones…) pour identifier les zones du réseau les plus risquées et guider ainsi les équipes travaux.
MAINTENANCE PRÉDICTIVE : UN PROBLÈME SCIENTIFIQUE COMPLEXE
Une des difficultés majeures est de déployer des outils de machine learning avancés tout en restant au plus proche de l’expertise de nos interlocuteurs : la réussite de ces projets repose sur une collaboration étroite entre data-scientists et opérationnels. Ainsi la prédiction d’incidents pose plusieurs questions : Comment conserver un vrai sens métier dans la résolution du problème et les métriques d’évaluation ? Comment modéliser des évènements rares sans perdre de vue les biais introduits par les hypothèses de modélisation ? Comment valider les résultats du modèle avec les retours terrain ?
DE LA MODÉLISATION AVANT TOUT
Une approche trop courante en Machine learning, consiste à transcrire le problème en une modélisation binaire, comme par exemple spam/non-spam, incident/non-incident. La majorité des algorithmes s’applique alors : il suffit de quelques minutes ensuite pour entraîner un random forest ou un GBM et tracer ensuite une courbe ROC.
La complexité de cette démarche réside dans la traduction du problème en une matrice de features (variables numériques) et des étiquettes 0 et 1. Dans le cas de prédiction d’incidents, le plus naturel est de définir 1 comme la survenue d’incident et 0 comme la non-survenue (« non-évènement »). Une granularité doit ensuite être choisie : Qu’est-ce qu’une « observation » ? En particulier l’observation d’un non-évènement peut poser problème. On est ainsi amenés à tronçonner l’espace-temps : Par exemple une observation est définie par l’observation ou non d’un incident sur un tronçon de 3km pendant une fenêtre glissante de 3 mois…
Ainsi, un énoncé simple se transforme rapidement en une modélisation qui requiert de nombreuses hypothèses. La difficulté apparaît généralement lors de l’évaluation du modèle : que signifie pour un interlocuteur métier d’avoir un lift à 2 ou à 3 ? Ou un ROC à 0,7 ? D’autant que ces valeurs dépendent intrinsèquement de la modélisation…
DÉFINIR EN PREMIER LIEU LES MÉTRIQUES
Avant d’avancer, il faut savoir vers quoi. Comment va être utilisé le résultat ? Notre modèle doit aider les acteurs de la maintenance à savoir quels sont les portions de voie à risque et à quel moment de l’année – la prédiction étant principalement utilisée pour la maintenance à long terme et non la prévision à très court terme. Il faut donc attribuer une note de risque à chaque point du linéaire. L’utilisateur sera satisfait si les incidents se produisent effectivement dans les zones notées comme risquées. Ce raisonnement nous permet de mettre en place deux métriques :
-
La courbe de lift, définie de manière assez classique : on confronte le nombre d’incidents au-dessus d’une note de risque (par exemple 0,5) à la proportion du réseau au-dessus de cette note. En faisant varier le seuil, on obtient bien une courbe avec une interprétation directe. Par exemple : « 50% des incidents se concentrent sur 10% du réseau le plus risqué ».
-
La courbe de précision: on confronte le rapport du nombre d’incidents détectés sur la proportion du réseau surveillée par rapport à la moyenne. Un point de la courbe s’interprète encore directement : «Les 10% les plus risqués du réseau sont 12 fois plus dangereux que la moyenne. »
MODÈLE BAYÉSIEN NAÏF
Les scores d’un algorithme sont souvent liés à une probabilité. Le problème s’apparente ici à la recherche de la distribution d’une seule classe : la survenue d’incident. On peut l’aborder sous différents angles : rechercher le profil type de tronçon ‘sans risques’ ou au contraire le profil type des tronçons à risque. Une série d’outils sont alors disponibles, depuis le ‘one-class SVM’ aux auto-encodeurs, dont le dénominateur commun est de chercher à reproduire la distribution qui génère un jeu d’observations. Deux types de limites peuvent cependant apparaître : ces algorithmes utilisent souvent des espaces euclidiens (ou s’y ramènent par des techniques d’apprentissage de métriques ou de noyaux) ; de plus ils fonctionnent comme des boîtes noires. Nous avons donc ébauché une démarche plus simple à partir d’un autre modèle classique : l’algorithme « naïf bayésien ».
UN (PETIT) PEU DE MATHÉMATIQUES
Reformulons notre problème de maintenance prédictive : l’objectif est d’évaluer la probabilité d’occurrence d’un incident en fonction de certaines caractéristiques de la voie : son passé, sa typologie, le remblai, la météo de la localisation, etc.
La première étape consiste à bien déterminer l’espace des observations. Il existe deux dimensions : une géographique, la localisation le long de la ligne, et une temporelle, le mois de l’année. On raisonne de manière continue sur le linéaire, mais les calculs sont effectués au km près.
Deuxième étape : à un point donné (paire de coordonnées géographique et temporelle), on note Y l’occurrence d’un incident et X1, X2, …. Xn les différentes caractéristiques. Le niveau de risque associé à ce point s’écrit alors, dans l’hypothèse « naïve bayésien » (indépendance des Xi) :
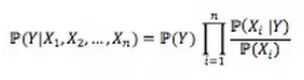
Explications :
P(Y/X1,X2,….Xn) est la probabilité d’occurrence d’un risque en un point sachant ses caractéristiques. il s’agit du niveau de risque associé à un point : C’est la valeur à estimer.
P(Y) est une probabilité de risque a priori, sans connaissance des caractéristiques de la voie.
P(Xi/Y) est la vraisemblance de la caractéristique Xi sachant qu’un incident s’est produit. Ainsi, si 60% des incidents ont lieu en forêt, la vraisemblance qu’un incident ait lieu en forêt est de 60%.
P(Xi) est la fréquence d’observation de cette caractéristique, qui doit pondérer la vraisemblance.
Par exemple, si les forêts couvrent 80% de l’espace, alors:
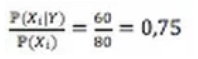
Cette fraction peut être interprétée comme la dangerosité liée à la caractéristique. Ainsi la forêt est une caractéristique qui multiplie le risque par 0,75 (donc le diminue) par rapport au risque moyen.
Rien de bien compliqué donc. Le facteur de risque final est le produit de chaque contribution au risque (la « dangerosité »). Ainsi n’a pas besoin d’être exprimé : seul le risque additionnel lié aux caractéristiques du la voie nous intéresse.
Rien de bien compliqué donc. Le facteur de risque final est le produit de chaque contribution au risque (la « dangerosité »).
Ainsi P(Y) n’a pas besoin d’être exprimé : seul le risque additionnel lié aux caractéristiques du la voie nous intéresse.
INTERPRÉTATION IMMÉDIATE
On comprend tout de suite l’intérêt de ce modèle : Il présente un aspect explicatif fort, ce qui intéresse l’acteur métier autant que les résultats afin d’appuyer ses décisions. La simplicité du modèle présente aussi l’avantage de permettre l’ajout de nouvelles features sans grand effort. Mais c’est aussi un inconvénient : moins performant, ce modèle est rapidement dépassé. Par ailleurs l’over-fitting n’est pas directement contrôlable de cette manière.
Cette modélisation possède un autre atout : contrairement aux modèles binaires décrits plus tôt, à aucun moment nous n’avons eu besoin de définir la notion de « non-évènement ». Cette complexité est en fait transférée dans le calcul d’un autre terme : P(X). En effet, son expression nécessite de connaitre la répartition dans l’espace des Xi.On notera que dans le naïve bayes binaire classique, ce terme n’est pas calculé (contrairement à P(Y)).
Le cadre théorique déployé par cette approche est donc particulièrement intéressant dans le cas d’évènement rares (peu observés) ou la richesse du modèle n’est pas nécessairement un atout, et que la compréhension métier des phénomènes est une priorité.

