MobileNet, optimisation de la convolution pour les réseaux de neurones embarqués.
Introduction
Aujourd’hui avec l’émergence de l’IoT et des systèmes embarqués, l’IA s’est introduite dans nos vies. Nos smartphones l’utilisent pour améliorer la qualité de nos photos, les voitures autonomes pour comprendre leur environnement. De manière générale, nos systèmes embarqués analysent de plus en plus d’images parfois volumineuses et gourmandes en ressource.
Les réseaux de neurones et plus spécifiquement les CNN – Convolution Neural Network sont particulièrement appréciés pour la classification d’image, la détection d’objet, de visage et la « fine-grained classification ». Cependant, ces réseaux de neurones effectuent des convolutions: des opérations très coûteuses en calcul et en mémoire. La classification d’image dans les systèmes embarqués représente donc un enjeu de taille dû aux contraintes matérielles.
Dans cet article, nous étudierons comment la Depthwise Separate Convolution proposée par Google en avril 2017 a permis d’optimiser la convolution en rendant son exécution plus rapide, moins gourmande en mémoire et donc moins consommatrice d’énergie qu’auparavant. Et cela, tout en conservant une bonne précision.
La Depthwise Separable Convolution est par exemple implémentée dans la famille de réseaux de neurones spécialisés en computer vision pour les systèmes embarqués : MobileNets.
La convolution standard dans les CNN
Pour comprendre comment la Depthwise Separate Convolution a optimisé la convolution, nous allons faire un rappel de la convolution standard tel qu’elle est classiquement utilisée dans les réseaux de neurones à convolution (CNN).
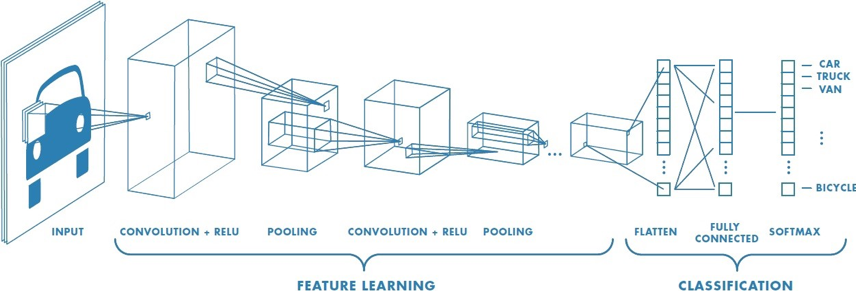
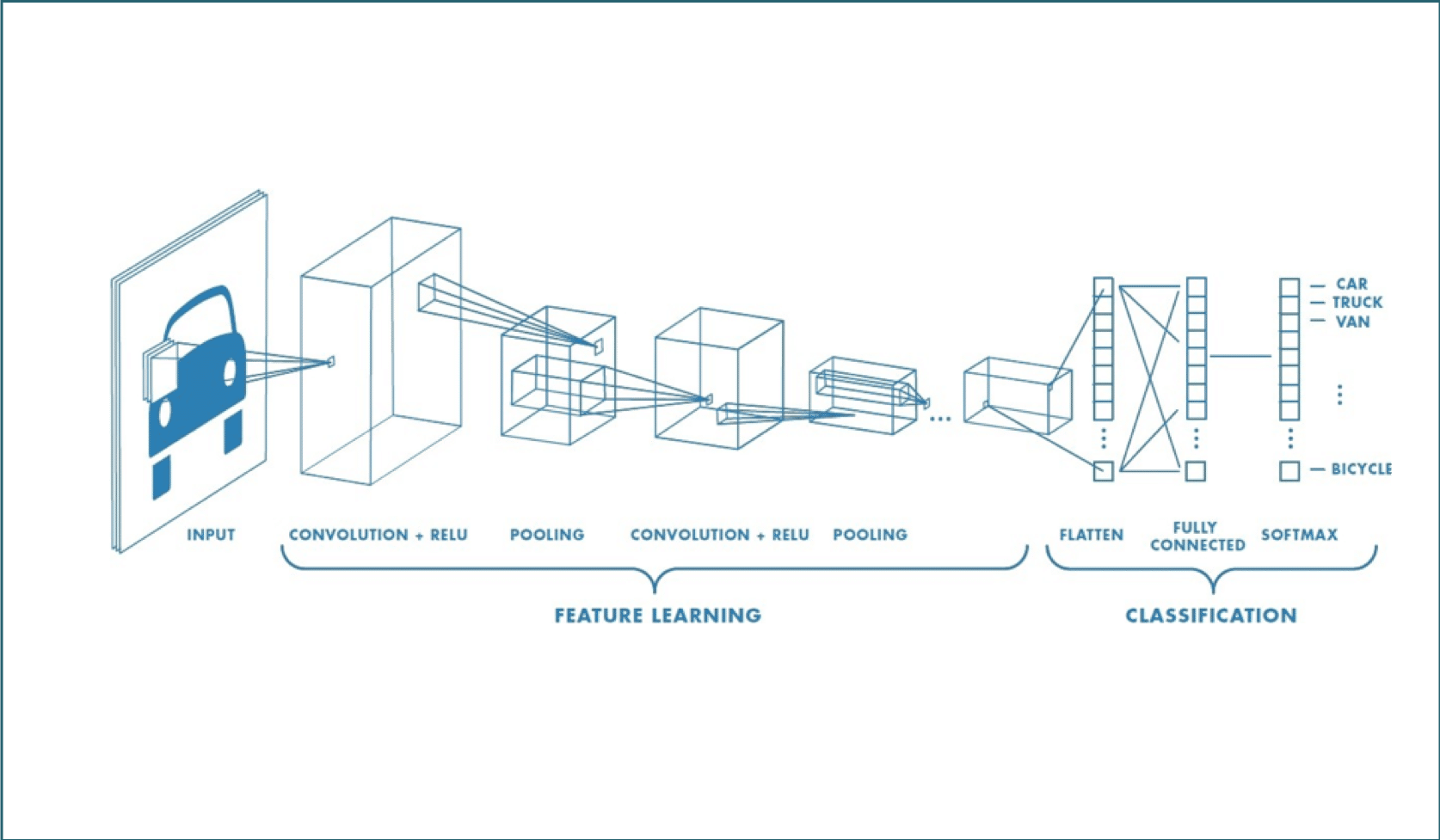
Un CNN est composé de plusieurs couches, comprenant la convolution, le ReLU, le Pooling, le Flattening, et la Full connection.
Afin de déterminer le contenu de l’image, celle-ci passe par deux phases :
- La phase de Feature Learning, est composée de plusieurs convolutions successives, et a pour but de faire sortir certaines caractéristiques de l’image.
- La phase de Classification, prédit si l’image en entrée est une voiture, un camion, un vélo, etc…
Une image en couleur est généralement composée de 3 canaux : rouge, vert et bleu. Chaque pixel de l’image est constitué d’une valeur entière comprise entre 0 et 255 sur chacun des canaux.
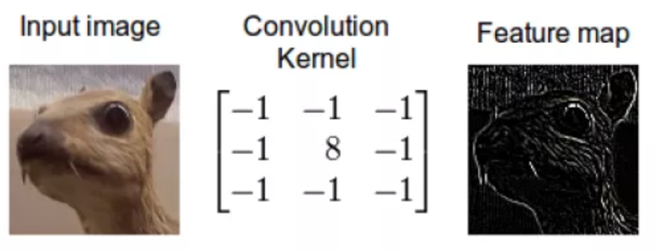
La convolution consiste à appliquer un filtre sur l’image. Pour cela un kernel se déplace sur la totalité de l’image d’entrée et agit comme un filtre afin de produire une image en sortie. Le kernel a pour but de détecter des formes particulières :
Concrètement la convolution est une somme de produits entre les valeurs RGB des pixels et les coefficients du kernel.
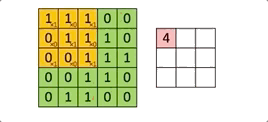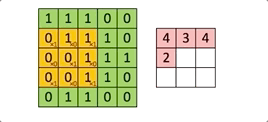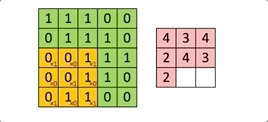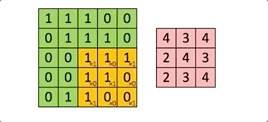
À chaque passage du filtre ![]() sur l’image, on calcule une somme de produits entre les valeurs de chaque canal et le kernel.
sur l’image, on calcule une somme de produits entre les valeurs de chaque canal et le kernel.
Par exemple, le premier calcule réalisé par le kernel est le suivant 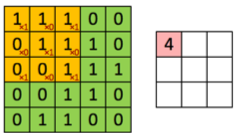
(1*1)+(1*0)+(1*1)+
(1*1)+(1*0)+(1*1)+
(1*1)+(1*0)+(1*1) = 4 => (ce qui fait 9 multiplications)
Dans les CNN, la convolution se fait en utilisant plusieurs kernels afin de capturer les particularités de l’image, comme ceci :
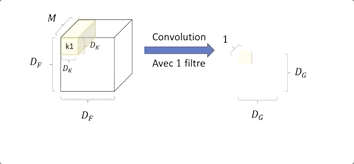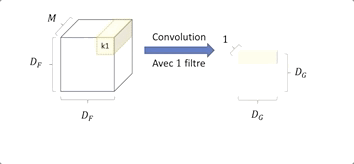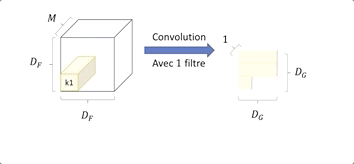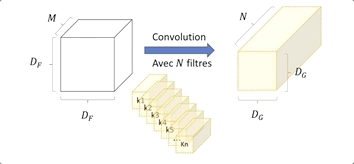
Nous avons une image en entrée de taille DF ⋅ DF et de profondeur M, (Métant le nombre de canaux de l’image) et un kernelKide taille DK ⋅ DK ⋅ M.
Le kernel Ki effectue une convolution sur tous les canaux, l’information est agrégée, on obtient donc en sortie une image de plus petite taille DG 2 et ayant une grande profondeur de N.
Voici la même convolution, vue d’un angle différent :
Depthwise Separable Convolutions
Dans MobileNet, la convolution est remplacée par une Depthwise Separable Convolution.
La Depthwise Separable Convolutions s’effectue en 2 étapes :
- Depthwise Convolution
- Pointwise convolution
Le terme Separable est lié à l’indépendance entre ces deux étapes.
Depthwise Convolution :
La Depthwise Convolution consiste à appliquer un filtre sur chaque canal, contrairement à la convolution classique qui applique un filtre sur l’ensemble des canaux.
Voici un exemple de Depthwise Convolution:
L’image initiale composée de trois canaux (RGB) subira pour chacun de ses canaux une convolution réalisée par trois kernels différents de taille fixe et de profondeur 1.
Chaque kernel (ici trois) va générer une image représentant une caractéristique particulière de l’image initiale. On obtient alors en sortie 3 images de plus petite taille. La Depthwise convolution n’augmente pas la profondeur de l’image.
Pointwise Convolution :
La Pointwise Convolution consiste à combiner les sorties de la Depthwise Convolution, elle est aussi appelée convolution 1×1.
Voici un exemple de Pointwise Convolution :
Dans cet exemple, un kernel de taille 1 ⋅ 1 ⋅ M réalise une convolution sur les 3 sorties simultanément de la Depthwise Convolution. En utilisant N kernels, on obtient en sortie de la Pointwise Convolution une image de profondeur N. La pointwise convolution augmente la profondeur de l’image.
Comparaison – Standard vs Depthwise Separate Convolution
Prenons en exemple une image en entrée de taille DF2 =52 composée de 3 canaux M = 3 , avec un kernel de taille DK2* 1 = 32 et l’on souhaite obtenir en sortie une image de taille DG2 32 et de profondeur N = 10:
Convolution Classique
Le nombre de multiplications réalisées par opération = DK2 • M → 32 • 3 = 18 → 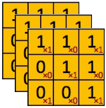
![]()
Le nombre de multiplications réalisées par un kernel sur l’ensemble de l’image = DK2 • M • DG2 → 32 • 3 • 32 = 243 → 
![]()
Le nombre de multiplications réalisées par N kernels sur l’ensemble de l’image = DK2 • M • DG2 • N → 32 • 3 • 32 • 10 = 2430 → 10x ![]() 10x
10x ![]()
La complexité de la convolution classique est donc de DK2 • M • DG2 • N
Depthwise Convolution (partie 1)
Le nombre de multiplications réalisées par opération = DK2 • 1 → 32 = 9 → 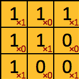
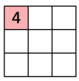
Le nombre de multiplications réalisées par un kernel sur un canal =DK2 • DG2 → 32 • 32 = 81 → 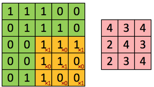
Le nombre de multiplications réalisées par un kernel sur un canal = DK2 • DG2 • M → 32 • 32 • 3 = 243 → 
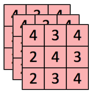
Pointwise Convolution (partie 2)
Le nombre de multiplications par opération = M → 3 → ![]()
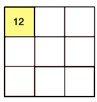
Le nombre de multiplications pour un filtre = DG2 • M → 32 • 3 = 27 → 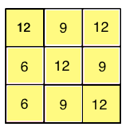
Le nombre de multiplications par N kernels sur l’ensemble des channels = DG2 • M • N → 32 • 3 • 10 = 270 → 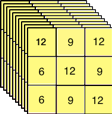
La complexité de Depthwise Separable Convolution
= Depthwise Convolution + Pointwise Convolution
= (DK2 • DG2 • M) + (DG2 • M • N ) = DG2 • M • (DK2 + N)
Résultats
Dans notre exemple, l’écart d’opération réalisé entre les deux types de convolutions est d’un facteur d’environ 5 (2430 vs 513).
En comparant les résultats obtenus avec et sans la Depthwise Separable Convolution sur des cas réels, on constate un gain de l’ordre de 8 à 9, cette réduction du nombre de calculs s’accompagne d’une réduction de l’accuracy de seulement 1% :

En calculant le ratio entre les deux types de convolution :

Avec une hauteur et largeur du kernel standard (entre 3 et 5) : plus la profondeur de l’image de sortie est grande, plus le gain sera important avec la Depthwise Separable Convolution.
Architecture des MobileNets
L’architecture des MobileNets est une architecture composée de 28 couches dont 13 Depthwise Convolution et 13 Pointwise Convolution :
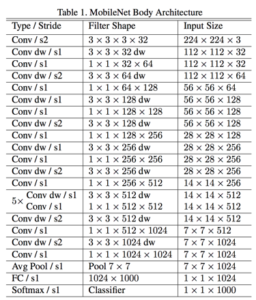
Par exemple : La dernière couche de convolution de MobileNet est une image de profondeur 1024.
Le gain par rapport à une convolution classique est donc de : ![]()
La convolution standard réalise donc 9 fois plus de calculs que la Depthwise Separable Convolution.
Conclusion
Pour résumer, la convolution classique applique des filtres sur tous les canaux d’une image et simultanément sur toute la profondeur de l’image, alors que dans la Depthwise Separable Convolution, les filtres sont appliqués indépendamment pour chaque canal puis recombinés, ceci étant possible grâce à la séparation du nombre de canaux d’entrée (M) et du nombre de canaux de sortie (N)
La séparation de la convolution en deux temps permet une économie de calculs, un allègement de la mémoire, ces optimisations ont également un bénéfice sur le temps de réponse et sur la consommation énergétique, tout en ayant un faible impact sur la précision, rendant son utilisation adaptée aux systèmes embarqués.