Abeille ou bourdon ? Activons les neurones (2/2)

Cet article termine ma présentation sur les réseaux de neurones à convolution et la compétition de classification d’images d’abeilles et de bourdons à laquelle j’ai participé il y a quelques mois. Dans le premier volet j’ai présenté la compétition et le fonctionnement des réseaux de neurones à convolution. J’aborde ici leur utilisation pratique pour la classification d’images, en commançant par les méthodes d’augmentation artificielle du jeu d’entraînement qui permettent une meilleure généralisation du modèle. La suite de l’article est consacrée à l’analyse des résultats fournis par les réseaux de neurones à convolution, dont l’interprétation est parfois complexe. Enfin la conclusion revient sur la compétition et évoque les méthodes utilisées par les vainqueurs. Cette présentation un peu technique est égayée par de nombreuses images pour le plus grand plaisir des amoureux des abeilles.
La recette standard de préparation des images
En partant d’un ensemble d’images étiquetées, une série d’opération est nécessaire à la préparation des données. Ce qui suit constitue la recette standard issue de mes recherches bibliographiques sur le sujet.
Normalisation
Avant l’entraînement, pour réduire l’impact la disparité des images (condition d’exposition, appareils différents, …) on normalise la valeur des pixels à travers l’ensemble d’entraînement.
Pour chaque couleur et chaque position de pixel i on calcule la moyenne μ et l’écart-type σ sur toutes les données d’entraînement à la même position, puis on centre et on réduit les valeurs des pixels :
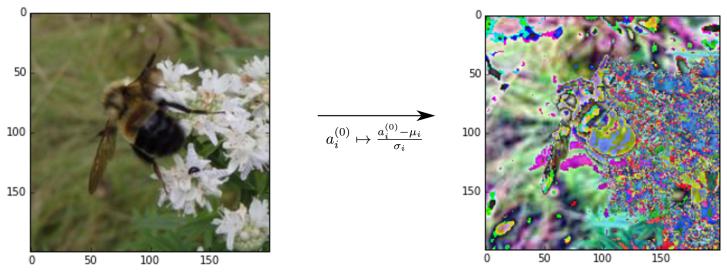
Après cette étape, ce ne sont plus les couleurs de l’image que l’on observe mais ses spécificités par rapport aux autres images du jeu de données.
Augmentation du jeu de données
Afin d’éviter le sur-apprentissage (« overfitting »), on peut enrichir artificiellement l’ensemble d’entraînement en faisant subir des transformations affines aux images (rotations, translations, réflexions et cisaillement) de manière aléatoire, et en sur-représentant les catégories rares (les abeilles dans notre cas).
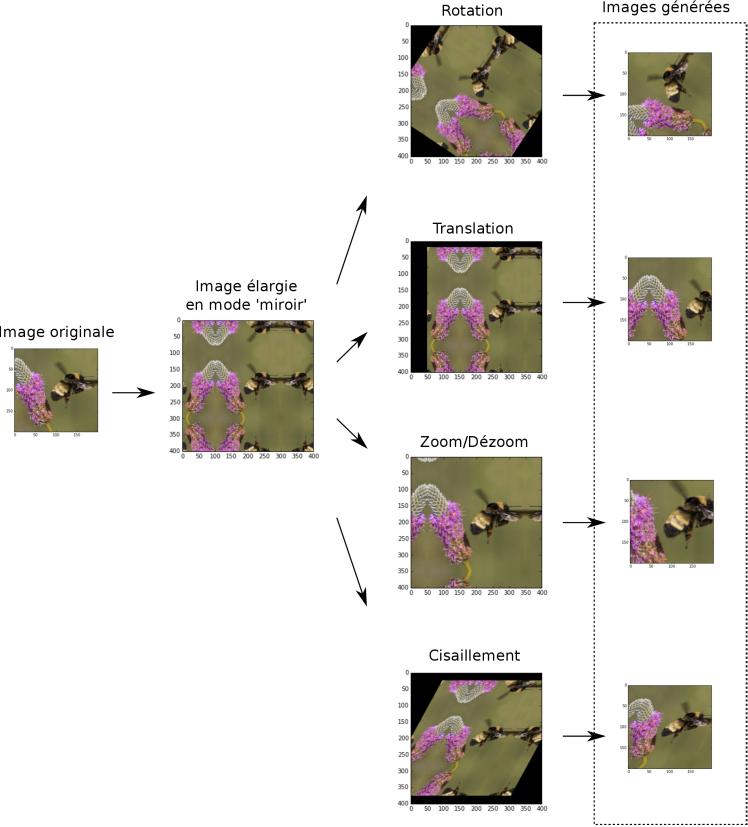
J’ai réalisé ces opérations avec le module images de scikit-learn, L’enrichissement artificiel du jeu d’entraînement permet de parer au sur-apprentissage inhérent aux réseaux de neurones, notamment sur les jeux d’entraînement de taille modeste (typiquement moins de 10 000 images). Les paramètres d’enrichissement tels que l’amplitude maximale des rotations ou le zoom maximal doivent toutefois être choisis de manière à ne pas trop altérer l’objet à classifier, auquel cas le réseau ne pourrait plus apprendre correctement. Au cours de la compétition j’ai affiné ces paramètres pour retenir finalement les transformations suivantes :
• rotation de 0 à 360°
• translation de plus ou moins 5 pixels
• zoom de plus ou moins 10 %
• pas de cisaillement
En ce qui concerne la sur-représentation des catégories rares, j’ai adopté une stratégie proposée par une équipe lors d’une précédente compétition de classification d’image. Cette stratégie consiste à tirer aléatoirement les échantillons qui constituent le batch à chaque étape de l’entraînement. On commence par tirer équitablement les classes, puis au fil de l’entraînement on diminue progressivement la probabilité de prendre une image de la classe minoritaire. J’ai opté pour la formule :

L’architecture du réseau de neurones
J’ai profité de cette initiation pour tester plusieurs architectures classiques de réseaux de neurones à convolutions. Il n’y en a pas énormément, dans la mesure où quelques architectures se sont imposées dans la littérature en termes de résultats. J’en ai surtout testées deux, l’architecture historique « AlexNet » d’Alex Krizhevsky et collaborateurs [1], et les réseaux très profonds (11 à 19 couches !) « VGG » proposés par des membres du Visual Geometry Group d’Oxford [2]. J’ai ensuite essayé de nombreuses architectures de mon cru, mais aucune n’est parvenue à rivaliser avec la performance des réseaux VGG. Ces derniers sont basés sur l’utilisation de filtres de petite taille (3×3) mais avec un très grand nombre de couches.
Les autres paramètres
Pour ce qui est de la descente de gradient stochastique qui réalise la mise à jour de poids, j’ai utilisé la méthode standard dumoment de Nesterov qui fait intervenir un deuxième paramètre « d’inertie » en plus du taux d’apprentissage. Selon une prescription classique du domaine, ces paramètres sont ajustés au cours de l’entraînement.
Ensemble de modèles
Une méthode standard pour réduire au maximum la variance d’un modèle prédictif consiste à agréger les prédictions de modèles indépendants. Ici nos modèles ne sont pas indépendants dans la mesure où ils sont entraînés sur les mêmes données. On peut néanmoins légèrement améliorer le score sur le jeu de test en remplaçant la probabilité prédite par un réseau de neurones par la moyenne des probabilités prédites par plusieurs réseaux de neurones différents. Une méthode plus élaborée consiste à entraîner un modèle qui prend en entrée les prédictions de différents réseaux de neurones ainsi que des paramètres généraux des images tels que la moyenne des valeurs de pixels et leur variance. Entraîner de tels « méta-modèles » peut conduire à une généralisation légèrement meilleure, mais dans mon cas n’a pas permis une amélioration significative des résultats. En entraînant des forêts aléatoires sur les prédictions de plusieurs réseaux j’ai obtenu des résultats qui n’étaient que légèrement meilleurs qu’en prenant le résultat de mon meilleur réseau.
Analyser un réseau de neurone à convolution :
Repérer le sur-apprentissage
L’apprentissage automatique est toujours menacé par le sur-apprentissage, mais dans le cas des réseaux de neurones qui sont très complexes, cette menace devient le problème numéro un. Pour repérer les situations de sur-apprentissage une première approche consiste à tracer l’erreur en fonction des itérations d’apprentissage, pour le jeu d’entraînement et un jeu de validation séparé.
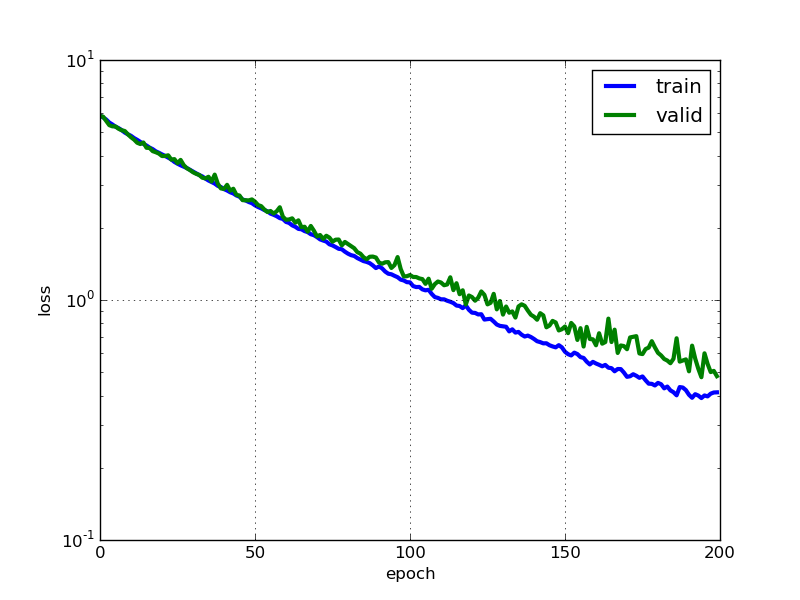
Illustration 1: Erreur en fonction de l’époque, pour le jeu d’entraînement (bleu) et le jeu de validation (vert). Une époque correspond à plusieurs itérations de la descente de gradient stochastique, tel qu’un nombre d’images égal au nombre d’images du jeu d’entraînement a été vu. Ce tracé montre un taux de sur-apprentissage acceptable, grâce au « drop-out ».
La technique du drop-out (et son évolution le max-out), qui « éteint » temporairement et aléatoirement certains neurones au cours de l’entraînement, est une très bonne solution pour parer au sur-apprentissage dans les réseaux de neurones. Cette méthode permet d’éviter la co-adaptation des neurones, c’est-à-dire d’empêcher les différents neurones d’apprendre les mêmes motifs. La figure 1 décrit l’évolution de l’erreur sur le jeu d’apprentissage et le jeu de validation au cours de l’entraînement. Le fait que les deux restent proches témoignent de l’utilité du drop-out comme régularisateur. Sans celui la diminution de l’erreur sur le jeu d’entraînement n’est pas suivie d’une diminution de l’erreur sur le jeu de validation. En sus du drop-out, j’ai eu recours à une faible régularisation L2 avec un paramètre λ=0.0005.
Repérer la co-adaptation des neurones
Une situation de sur-apprentissage peut se traduire par une co-adaptation des neurones, auquel cas différents filtres d’une même couche apprennent les mêmes motifs. On peut vérifier si c’est le cas en traçant les poids des filtres des différentes couches du réseau (Illustration 2).

Illustration 2: Poids des différents filtres de la première couche d’un réseau AlexNet au cours de l’entraînenemt. On voit que les filtres sont différents, ainsi il n’y a pas de co-adaptation des neurones et il est donc pertinent de poursuivre l’entraînement du modèle.
Tracés d’occlusion
Pour vérifier que le modèle repère l’objet pertinent au bon endroit dans les images, et donc que les bons motifs sont appris, on peut également dessiner les graphes d’occlusion (Illustration 3). Dans ceux-ci, on cherche les zones de l’image qui ont eu le plus de poids dans la prédiction du modèle, et on superpose le tracé de ces zones à l’image pour vérifier que ce sont bien les zones où sont présentes un insectes qui impactent la prédiction.

Illustration 3: Image d’occlusion. On voit ici que le modèle a bien appris les motifs caractéristiques pertinents, car les zones critiques sont situées à l’emplacement de l’insecte.

Illustration 4: Image d’occlusion. Exemple d’un modèle qui n’a pas appris l’ensemble des motifs pertinents. On voit que les zones critiques pour la prédictions sont trop localisées.
Conclusion :
La mise en place de toutes ces méthodes m’a permis d’atteindre une exactitude d’environ 95 % sur la classification des bourdons et abeilles (AUC-ROC de 96,54%). En reprenant simplement les méthodes standard dans la littérature on peut donc catégoriser les images très précisément. Ce niveau de précision m’a permis de me classer 10e sur 432 participants. Un article de blog publié par le second m’a permis de confirmer le fait que les scores très impressionnants (AUC-ROC = 99,56%) atteints par les meilleurs compétiteurs étaient rendus accessibles par l’utilisation de réseaux dont les poids sont pré-entraînés . Ce procédé consiste à initialiser les poids des premières couches avec les valeurs apprises sur un jeu d’image très large (de tels ensembles de valeurs sont mis à disposition par de nombreux groupes de recherche en vision par ordinateur : par exemple ici pour les poids du réseau VGG16 entraîné sur les données ImageNet). Moyennant l’utilisation de la même architecture on peut obtenir un réseau très performant en opérant quelques étapes d’entraînement à partir des poids pré-entraînés. L’utilisation de réseaux pré-entraînés est d’autant plus justifiée que le jeu de donnée est petit, car alors les motifs très généraux appris par le modèle pré-entraîné empêchent le sur-apprentissage.
Sources :
[1] : Article d’Alex Krizhevsky et collaborateurs sur la compétition ImageNet 2012 : http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
[2] : Introduction des VGG nets : http://arxiv.org/abs/1409.1556
[3] : Syndrôme d’effondrement des colonies d’abeilles : https://www.youtube.com/watch?v=GqA42M4RtxE#t=147
[4] : Site de la compétition : http://www.drivendata.org/competitions/8/
[5] : Cours de Stanford sur les ConvNets : http://cs231n.github.io/
[6] : Le repository github de mon code : https://github.com/wajsbrot/bees
[7] : Article de blog du second (Jan Hendrik Metzen aka ‘frisbee’) : https://jmetzen.github.io/2015-12-20/naive_bees.html
[8] : Drop-out : https://www.cs.toronto.edu/~hinton/absps/JMLRdropout.pdf
[9] : Max-out : http://jmlr.csail.mit.edu/proceedings/papers/v28/goodfellow13.pdf

