Haro sur la fraude !

La demande pour des systèmes évolués de lutte contre la fraude est de plus en plus forte. Le croisement et l’analyse de volumes importants de données permis par la Data Science ont ouvert de nouvelles possibilités dans la conception de tels systèmes. L’objet de cet article est de décrire notre démarche lors du développement de ces systèmes de détection de fraude chez nos clients.

La pertinence des approches que nous allons décrire dépend du cas d’usage ainsi que de la nature des données et de la cible, la définition de la fraude variant en fonction du métier du client. Pour commencer de tels projets, il faut disposer d’une base historisée de données clients (données bancaires, données de contacts, etc.), la cible pouvant être bien définie (voir sections de l’approche supervisée et semi-supervisée) ou non (voir section de l’approche non-supervisée).

Si la cible est bien définie, adopter une approche supervisée semble naturel. Nous ne détaillerons pas les phases de nettoyage et préparation des données hormis deux points dont l’impact positif sur la performance du système a souvent été noté :

• La transformation des variables catégorielles : si l’on dispose de variables catégorielles dans la base de données, la performance du modèle peut fortement dépendre de la méthode de traitement de ces variables. Nous avons le plus souvent testé trois méthodes :

1. Une projection de la cible sur la variable. On obtient ainsi le pourcentage de fraudeurs appartenant à chaque catégorie ;

2. Une sélection des catégories les plus fréquentes : le nombre de catégories retenues est arbitraire, les autres valeurs non retenues sont fusionnées dans une catégorie « autre » ;

3. Une sélection des catégories où le ratio du taux de fraude constaté rapporté au taux de fraude sur la population totale est le plus élevé. Il s’agit en quelque sorte d’une mesure de l’écart à une distribution homogène de la fraude dans la population.

• Une fois les tables formatées et les variables explicatives créées, on peut tester plusieurs modèles, comme par exemple les forêts aléatoires et le GBM. Si le langage utilisé pour le développement des prototypes est R, il est important de noter que la parallélisation des algorithmes n’est pas implémentée de manière native, ce qui peut conduire à des problèmes de lenteur des calculs lors de l’entraînement des modèles. Lors de nos différentes missions, plusieurs approches utilisant les packages de parallélisation « foreach » et « doMC », ainsi que la méthode « parRF » du package « caret », ont été testées pour les forêts aléatoires, avec une amélioration appréciable de la vitesse des calculs mais souvent insuffisante. L’utilisation de la plateforme H2O, qui intègre de manière native la parallélisation de plusieurs algorithmes standards de machine learning (dont les forêts aléatoires et le GBM) a permis dans certains cas un gain de temps de l’ordre d’un facteur 10.

APPROCHE NON-SUPERVISÉE DE LA DÉTECTION DE LA FRAUDE

L’approche supervisée détaillée dans la section précédente implique qu’un nombre suffisant de cas de fraudes avérées a été détecté et répertorié. Lorsque les processus de lutte contre la fraude sont encore naissants ou peu liés aux données, il devient nécessaire d’adopter une approche non supervisée.

Le postulat courant pour appliquer cette approche à la détection de fraude est d’assimiler la fraude à une anomalie. On considère donc que, par nature, la fraude tend à dévier du comportement dit « normal » ou commun. La détection d’anomalies consiste donc souvent à faire le portrait en creux d’une donnée dont l’on ne connaît pas les caractéristiques, à l’inverse des techniques basées sur des règles métier qui nécessitent de connaître très précisément ces caractéristiques.

Comment définir alors ce qui est « normal » ? Dans l’arsenal du non-supervisé, le clustering est une première approche intéressante pour s’attaquer à ce concept un peu flou de normalité. Pourtant, chercher à mettre chaque individu dans un groupe peut paraître contre-intuitif pour détecter ceux qui sont éloignés de ces mêmes groupes. Mais en optimisant la formation des clusters, on pose justement l’hypothèse que l’individu a été classé dans le groupe lui convenant le mieux : si l’individu se trouve loin de ses pairs, il sera de fait déclaré comme un cas anormal.

Le clustering peut être réalisé de différentes manières – n’hésitez pas à aller jeter un œil sur notre article sur le sujet – mais au-delà de l’algorithme choisi pour la construction des clusters, la technique que nous employons est assez générique et consiste à retirer itérativement les éléments les plus éloignés du centroïde de leur cluster (ou plus généralement de l’élément représentatif du cluster) jusqu’à ce que les clusters n’évoluent plus (au regard de l’indice de Rand par exemple).

Les résultats obtenus à l’aide de cette méthode permettent ainsi de faire remonter les anomalies statistiques. Cependant, l’utilisation du clustering empêche intrinsèquement de trouver des cas de fraude qui seraient similaires et correspondraient donc eux-mêmes à un cluster. Ces difficultés peuvent être levées avec l’utilisation de l’apprentissage semi-supervisé. En effet, ces algorithmes permettent, dans le cas où l’on sait identifier les dossiers normaux, de construire un modèle du comportement normal pour ensuite détecter les comportements qui en dévient.

APPROCHE SEMI-SUPERVISÉE DE LA DÉTECTION DE LA FRAUDE

Nous détaillerons dans cette section un exemple d’approche semi-supervisée basée sur une architecture spécifique de réseaux de neurones, celle des autoencodeurs.

Un autoencodeur est un réseau de neurones possédant une architecture en entonnoir :

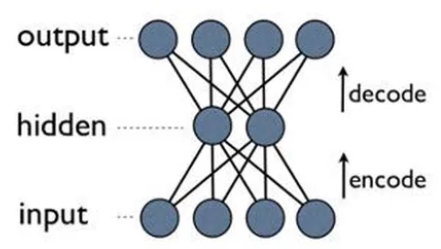
Le nombre de sorties est égal au nombre d’entrées du réseau. Son objectif est d’approximer la fonction identité, avec la contrainte que la couche intermédiaire contienne moins de neurones que les couches d’entrée et de sortie. La zone entonnoir constitue ainsi une représentation de dimension réduite des variables d’entrée.

Si l’on entraîne ce réseau (via l’algorithme classique de backpropagation) uniquement sur des évènements normaux, le réseau apprendra à approximer la fonction identité sur de tels évènements. La représentation de dimension réduite dans la couche intermédiaire induira nécessairement des erreurs dans la reconstruction du signal d’entrée sur la deuxième moitié du réseau. Ces erreurs seront d’autant plus importantes que le signal en dimension réduite s’éloigne du comportement normal, fournissant ainsi via un classement par erreur décroissante un système de détection d’anomalies.

Afin de quantifier la performance du modèle, on trace l’histogramme des erreurs de reconstruction pour les dossiers non frauduleux et les dossiers frauduleux (voir les deux illustrations).

Intuitivement, si les deux courbes sont très distantes (illustration à droite), cela signifie que des grandes erreurs correspondent systématiquement à de la fraude, d’où un système très performant de détection de cette fraude par calcul de l’erreur de reconstruction. Dans le cas contraire (figure à gauche), le réseau possède une représentation des dossiers qui ne distingue pas de manière efficace les cas frauduleux des cas non frauduleux.

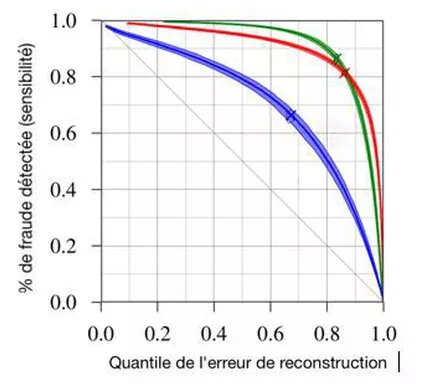
Cependant, se fier à la représentation graphique de ces courbes induit souvent en erreur. On peut construire une métrique rigoureuse de l’écart entre les courbes en classant tous les dossiers (frauduleux ou non) par valeur croissante de l’erreur de reconstruction, et en calculant, pour chaque quantile de l’erreur de reconstruction le pourcentage de la fraude détectée. On obtient ainsi une courbe similaire à la courbe de ROC (voir graphique ci-dessous). Le modèle aléatoire correspond alors à la diagonale (à X% de la population, on détecte 1-X% de la fraude), tandis que l’aire sous la courbe fournit une indication de la performance similaire à l’aire sous la courbe de ROC (il s’agit en réalité d’une excellente approximation de cette dernière pour une cible rare).

Conclusion

Nous avons détaillé dans cet article plusieurs approches pour le développement de systèmes de lutte contre la fraude. Le plus souvent, ces systèmes ne sont pas amenés à remplacer l’expertise humaine mais à lui fournir des outils performants pour faire face à l’augmentation des volumes de données à traiter dans le processus de digitalisation. L’importance de la transformation de la chaîne opérationnelle à mettre en place pour intégrer ces nouveaux systèmes dans les processus existants dépend beaucoup du secteur. La capacité à mettre des systèmes de détection de fraude en production est donc un élément de décision au moins aussi important que la performance des techniques utilisées. Nul doute cependant que la Data Science peut contribuer à la sécurisation et la fluidité d’une relation-client de plus en plus digitale !