Abeille ou bourdon ? Activons les neurones

La plateforme de data science éthique DrivenData.org a lancé en septembre une compétition de classification d’images d’abeilles et de bourdons, qui s’est terminée le 3 décembre dernier. J’ai profité de cette occasion pour me frotter aux réseaux de neurones à convolutions, omniprésents dans la vision par ordinateur depuis plusieurs années. Cet article présente la compétition et ses enjeux, expose ensuite brièvement le fonctionnement des réseaux de neurones à convolutions, et aborde enfin leur implémentation pratique.
INTRODUCTION – LA PLATEFORME DRIVENDATA.ORG ET LA COMPÉTITION NAIVE BEES CLASSIFIER
DrivenData.org est un alter-ego de Kaggle, plus récent et pour l’instant moins connu que ce dernier. L’accent y est mis sur les sujets d’intérêt général tels que l’accès à l’eau potable, l’éducation ou encore le gaspillage alimentaire. La compétition « Naive Bees Classifier » a démarré début septembre et s’est terminée le 3 décembre dernier, avec à la clé un prix de cinq mille dollars réparti entre les trois premiers. J’y ai participé sous le pseudonyme Wajsbrot.
Le but de la compétition était de produire un programme qui distingue les photos d’abeilles de celles de bourdons. Derrière cette préoccupation en apparence oiseuse se cache un objectif d’envergure. Les abeilles sont aujourd’hui largement menacées (5 millions de ruches sur la planète en 1988 contre 2,5 millions seulement aujourd’hui), notamment par le syndrome d’effondrement des colonies d’abeilles dont la cause est encore mal connue. Pour étudier ce mal il faut comprendre où les abeilles disparaissent, et donc il faut pouvoir les recenser. Pour ce faire, une idée consiste à mettre à disposition du public une application mobile avec laquelle les utilisateurs signalent la présence d’abeilles à leur position, par exemple en les prenant en photo. Cependant il est difficile pour les utilisateurs de distinguer une abeille d’un bourdon, d’où la nécessité d’un programme qui réalise cette tâche.
L’intérêt est de taille, car au-delà de la préoccupation gourmande pour le miel, la disparition des abeilles implique 50 % de pollinisation en moins. On estime qu’un plat sur trois nécessite l’intervention des abeilles, et que le marché correspondant s’élève à 265 milliards de dollars ; je vous laisse imaginer les conséquences de leur disparition.
ABEILLE / BOURDON / GUÊPE / FRELON : QUI EST QUI ?
Si comme moi vous avez connu de nombreux débats autour du barbecue sur « qui perd son dard et meurt après , qui pique et qui ne pique pas » parmi tous ces insectes, vous ne serez pas fâchés de pouvoir briller au prochain repas estival.

Illustration 1: Le bestiaire
En résumé, le bourdon est plus gros et plus touffu et ne meurt pas après avoir piqué, contrairement à l’abeille dont le dard est attaché à l’abdomen. La guêpe est lisse, et pique abondamment et plus agressivement. Les frelons sont quant à eux beaucoup plus gros et ne piquent qu’en situation de défense. Enfin, toutes ces espèces ont la bienveillance de contribuer à la pollinisation.
LE JEU DE DONNÉES
Dans le cadre de la compétition, près de cinq mille images d’abeilles et bourdons sont mises à disposition, elle sont toutes au format jpg à la résolution 200×200.
-
Jeu d’entraînement : 3 142 images de bourdons et 827 d’abeilles
-
Jeu de test : 992 images
Le classement est déterminé à partir de la probabilité prédite que l’image soit celle d’un bourdon, pour les 992 images du jeu de test. Pour chaque photo une prédiction de 1 indique un bourdon de manière certaine, 0 celle d’une abeille, et 0,5 trahit une indécision totale. Le score des prédictions est donné par l’aire sous la courbe ROC qui est une métrique très conventionnelle pour la classification binaire.

Illustration 2 : Abeille (HoneyBee)

llustration 3 :Bourdon (BumbleBee)
LES RÉSEAUX DE NEURONES À CONVOLUTION
Pour catégoriser les images, le modèle des réseaux de neurones à convolution s’est largement imposé depuis 2012. Cette année-là, Alexander Krizhevky et ses collaborateurs ont gagné la compétition de classification d’images ImageNet avec une confortable avance en réutilisant ce type de réseaux de neurones [1], quelque peu tombés en désuétude depuis les travaux de Yann LeCun sur la lecture automatisée de chiffres manuscrits en 1989.
Les images décompressées sont stockées sous forme de tableaux de pixels, la couleur de chaque pixel étant déterminé par 3 valeurs qui correspondent à l’intensité de rouge, de vert et de bleu (RGB) sur le pixel considéré. Une image en couleur de résolution 200×200 est donc définie par 200x200x3 = 120 000 nombres, autrement dit la dimension d’entrée du modèle est 120 000. C’est beaucoup. D’autant plus que l’expérience montre que la classification d’image ne peut se faire avec un modèle simple tel qu’une régression logistique. Seuls des réseaux de neurones profonds (voir l’article de blog de Nicolas Gibaud datant du 16 juin 2015) sont à même de réaliser cette tâche de manière satisfaisante.

Illustration 4 : Décomposition d’une image RGB
Les réseaux de neurones artificiels permettent – entre autres – aux ordinateurs de catégoriser les objets présents dans une image. Tandis que la distinction visuelle entre un bourdon et une abeille peut sembler évidente à un humain éclairé, l’ordinateur ne voit dans l’image qu’un ensemble très grand de nombres. Extraire les caractéristiques qui trahissent la présence d’une abeille dans ces images demande une série de transformation qui sont réalisées par les couches successives du réseau de neurones.
Je ne rappellerai que brièvement le principe des réseaux de neurones ici, et je renvoie le lecteur intéressé au cours de l’université de Stanford correspondant.
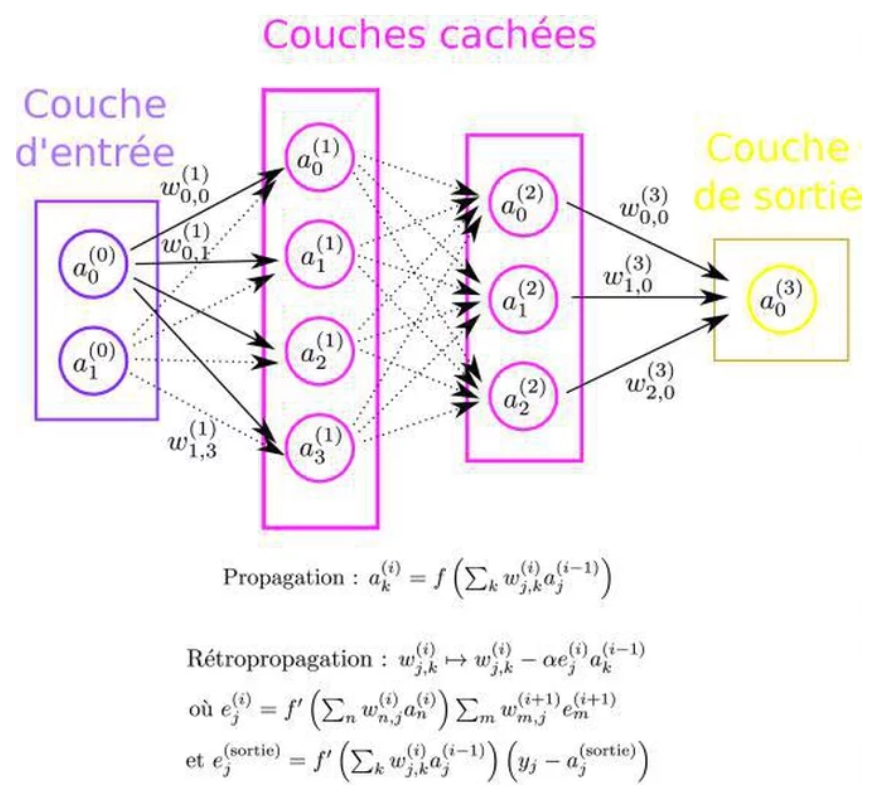
Illustration 5 : Réseau de neurones
Le réseau de neurones « standard » (i.e. sans convolutions) est dépeint sur l’illustration 4. Dans le cas qui nous intéresse, le nombre de neurones d’entrée est donné par le nombre de pixels à traiter, la sortie au nombre de catégories à prédire, et le modèle est défini par le nombre de couches cachées, le nombre de neurones de chacune d’entre elles, et la fonction d’activation fqui introduit la non-linéarité dans le modèle et permet de calculer le degré d’activation aj(i) du j-ème neurone de la couche numéro i.
Pour rappel, les poids du réseau wi,j(k) sont initialisés aléatoirement (généralement selon la distribution préconisée par Xavier Glorot et Joshua Bengio) puis déterminés par descente de gradient de manière à minimiser la fonction d’erreur (l’entropie croisée dans notre cas). Les degrés d’activation aj(i) sont tous obtenus par propagation de couche en couche via la formule indiquée sous la figure, et la dérivée qui intervient dans la descente de gradient est calculée par rétroprogation du gradient.
Le nombre de poids à déterminer de la sorte augmente rapidement avec le nombre de neurones du modèle (i.e. le nombre de « flèches » augmente rapidement avec la complexité du modèle sur l’illustration 5). Or, comme je l’ai dit précédemment, on sait d’expérience que la classification d’image nécessite un modèle complexe et donc un nombre important de neurones. L’optimisation d’un tel modèle serait impossible en pratique avec un réseau de neurones classique tel que celui présenté sur la figure 5. Les réseaux de neurones à convolutions viennent palier à cette lacune de manière astucieuse en imposant des contraintes sur les poids, et permettent de réduire drastiquement la dimension de l’espace de paramètres impliqué. L’astuce principale consiste à utiliser « l’invariance par translation » inhérente à la classification d’image.
RÉSEAUX DE NEURONES ET IMAGES : LES COUCHES CONVOLUTIONNELLES
Les réseaux de neurones à convolution fonctionnent par agglomération progressive de « motifs ». Les couches successives sont définies par des « filtres » de petite taille (typiquement 3×3 jusque 11×11), qui apprennent chacun à reconnaître un motif dans l’image. La reconnaissance d’un motif par un filtre se traduit par une activation importante dans la feature map correspondante. L’ensemble des feature maps (ou « kernels ») constitue une couche convolutionnelle. Le principe de fonctionnement d’une couche de convolution est illustré sur la figure 6, je ne décrirai pas le fonctionnement des couches de « pooling » qui sont le deuxième ingrédient essentiel des réseaux de neurones à convolution, et je renvoie à nouveau le lecteur intéressé à la littérature pertinente.
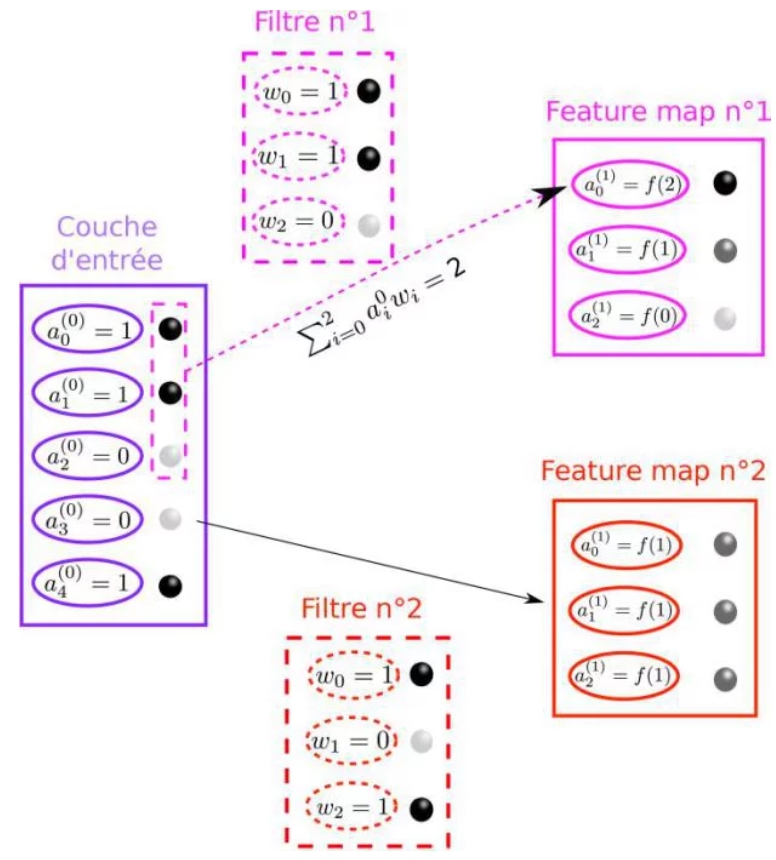
Illustration 6: Principe de fonctionnement d’une couche convolutive à deux filtres. Les images sont remplacées par des motifs de billes noires (a=1) et blanches (a=0) à titre d’illustration. Le filtre numéro 1 est fortement activé en haut de « l’image », car dans cette zone le filtre correspond au motif repéré (bille noire dans la feature map n°1). A l’inverse le motif du filtre 2 (noir-blanc-noir) n’est pas repéré dans « l’image » d’entrée, les neurones de la feature map n°2 sont donc peu activés (boules grises). Les deux feature maps constituent la première couche convolutionnelle.
La figure 7 montre des motifs typiques que la première couche d’un réseau de neurones à convolutions apprend à reconnaître. Ce sont des formes vagues, dont l’arrangement peut former des formes plus complexes (voir la figure 8).

Illustration 7: Motifs appris par les 64 filtres qui constituent la première couche du réseau AlexNet (motifs 11×11) entraîné sur le jeu de données ImageNet. Les motifs représentés sont les arrangements de pixels pour lesquels l’activation des neurones est maximale.
Les réseaux de neurones à convolution sont calqués sur le fonctionnement de notre appareil visuel. Au lieu de rechercher directement l’arrangement de pixels qui trahit la présence d’une abeille dans toute l’image, notre œil cherche des « arrangements de motifs ». Des rayures oranges et noires, proches de six pattes, proches d’antennes, etc. On peut s’inspirer de ce fonctionnement pour adapter les réseaux de neurones aux problèmes « invariants par translation » tels que la classification d’image. La première couche de ce réseau apprend à reconnaître des motifs de petites tailles, la couche suivante des motifs de motifs, etc. Ainsi les couches successives du réseau apprennent à reconnaître des arrangements de motifs de plus en plus élaborés, jusqu’à distinguer simplement une abeille d’un bourdon.

Illustration 8: Exemple d’arrangements de motifs pour un problème de classification de visages humains. La figure de gauche représente les motifs appris par la première couche du réseau et les figures suivantes représentent les motifs appris par des couches plus profondes du réseau.
LES RÉSEAUX DE NEURONES EN PRATIQUE : LES BIBLIOTHÈQUES DE « COMPILATEURS D’EXPRESSION MATHÉMATIQUES »
Malgré la réduction drastique du nombre de poids à déterminer dans un réseau de neurones à convolution par rapport à son équivalent classique, le nombre de poids reste de l’ordre de la dizaine de millions, et il est donc impensable d’entraîner le réseau sans une carte graphique performante, qui permet la parallélisation massive des calculs. J’ai eu recours à des instances g2.2xlarge sur Amazon Web Services (AWS), mais j’aurais pu faire la même chose avec un ordinateur muni d’une carte graphique.
Pour utiliser des réseaux de neurones sans avoir à se soucier de la parallélisation, on utilise généralement des bibliothèques de deep learning telles que Torch, TensorFlow, Caffe ou Theano (voici un benchmark pour les curieux). Pour ma part j’ai utilisé Theano et sa « surcouche » Lasagne, qui permet de définir des couches de neurones simplement. L’avantage de ces bibliothèques tient à leur capacité à :
-
Optimiser automatiquement les séquences de calcul à travers tous les réseaux
-
Calculer symboliquement la différentielle impliquée dans la descente de gradient
-
Utiliser la carte graphique pour les calculs, avec une simple option
Les codes correspondants sont accessibles sur mon dépôt github.
AU PROCHAIN ÉPISODE : LE VIF DU SUJET
Cette introduction rudimentaire mais somme toute conséquente à la compétition et aux réseaux de neurones à convolution me permettra de rentrer dans le vif du sujet dans un prochain article. Dans celui-ci je décrirai les architectures classiques de réseaux de neurones à convolutions, le problème important de l’augmentation du jeu de données, ainsi que les méthodes d’ensemble de modèles. Enfin je dresserai le bilan de la compétition et évoquerai les méthodes utilisées par les autres compétiteurs. Restez attentifs au blog, la suite sera riche en images !
SOURCES :
[1] : Article d’Alex Krizhevsky et collaborateurs sur la compétition ImageNet 2012 : http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
[2] : Introduction des VGG nets : http://arxiv.org/abs/1409.1556
[3] : Syndrôme d’effondrement des colonies d’abeilles : https://www.youtube.com/watch?v=GqA42M4RtxE#t=147
[4] : Site de la compétition : http://www.drivendata.org/competitions/8/
[5] : Cours de Stanford sur les ConvNets : http://cs231n.github.io/
[6] : Le repository github de mon code : https://github.com/wajsbrot/bees

