Comment s'adapter à l'évolution de la fraude ?

Le nombre de transactions bancaires sur internet augmente, et le nombre de fraudes également. De plus, les fraudeurs contournent sans cesse les barrières de protection mises en place par les banques. Comment éviter qu’un modèle anti-fraude devienne obsolète dès sa mise en production ? Voici quelques éléments de réponse apportés par l’apprentissage adaptatif.

Comment la banque s’adapte-t-elle à la fraude ?

Une banque doit pouvoir gérer des centaines de millions de transactions par an. Parmi toutes ces transactions, environ une sur mille est une fraude.

Le point de vue du fraudeur

Une fraude typique consiste à obtenir les codes carte bleue d’une victime, à effectuer des achats en ligne à sa place et à revendre les produits obtenus sur le marché noir. Le fraudeur a tout intérêt à maximiser son gain, c’est-à-dire à perpétuer les transactions frauduleuses sans se faire bloquer par la banque.

Le point de vue de la banque

De son côté, la banque analyse de manière semi-automatique toutes les transactions effectuées. Un système de détection (souvent un système de règles) bloque les transactions suspectes. Des experts en sécurité les analysent ensuite en détails, et peuvent confirmer ou infirmer la fraude en contactant directement le client. Toute cette étape est en réalité une étape de labellisation des transactions (voir Figure 1).

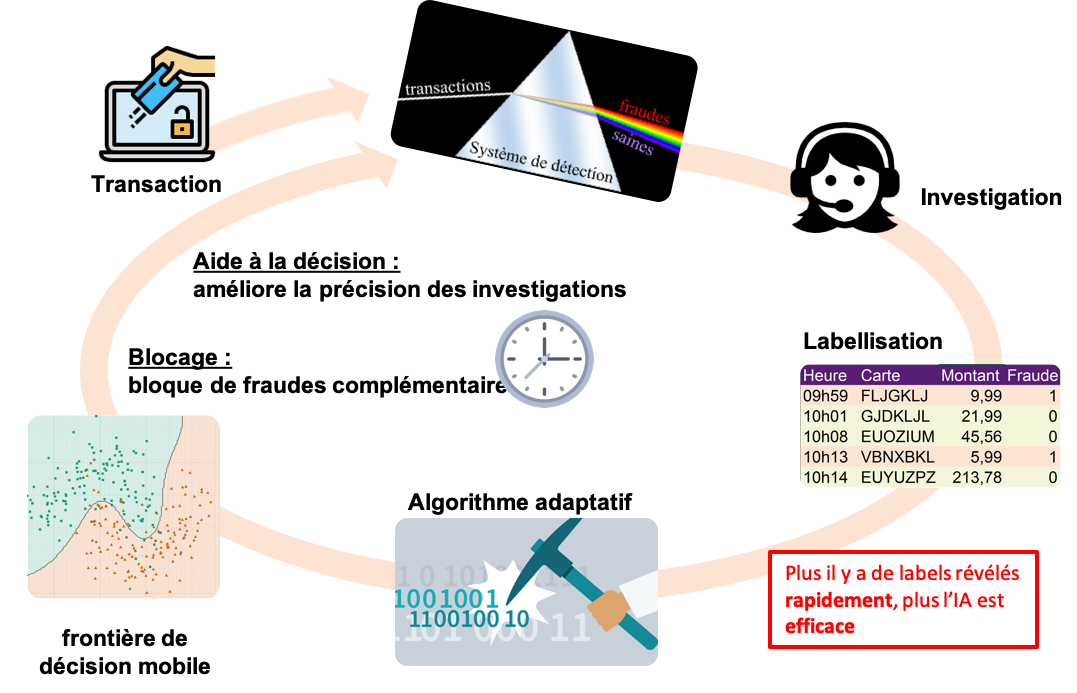
Figure 1 – Le cycle de vérification d’une transaction. Lorsqu’une transaction est émise, elle est analysée par un système de blocage. Les transactions bloquées sont ensuite analysées par des experts en sécurité qui labellisent lesdites transactions. Un modèle de machine learning peut alors s’entraîner sur les transactions labellisées et venir nourrir le système en place.

Comme dans tout jeu du chat et de la souris, la banque et les fraudeurs se livrent une guerre technologique sans merci. Le comportement des fraudeurs change sans cesse et celui de la banque également. Dans ce contexte changeant rapidement (parfois en l’espace de quelques heures), la plupart des modèles de détection de fraude voient leur performance chuter : on parle de dérive des modèles.

Qu’est-ce qu’une dérive de modèle ?

Persistance rétinienne infinie

Par abus de langage, on parle de dérive de modèle dès que les performances décroissent dans le temps après la mise en production. En réalité, le modèle ne dérive pas : il a photographié l’état de la fraude à la date d’entraînement et ne s’est donc pas adapté à l’évolution des patterns de fraude. En toute rigueur, c’est donc la donnée qui a dérivé (voir Figure 2). On parle alors de dérive conceptuelle (concept drift) [1]. Imaginez vous en train de regarder un film avec une persistance rétinienne infinie : le générique de début se mélangerait à la première scène, puis à la deuxième jusqu’à l’obtention d’une purée visuelle où plus aucun élément n’est intelligible (exemple sur le film Mary Poppins). C’est un peu ce que ressent un modèle statique entraîné sur un flux dynamique. Il faut donc passer d’une vision photographique de la donnée à une vision cinématographique.

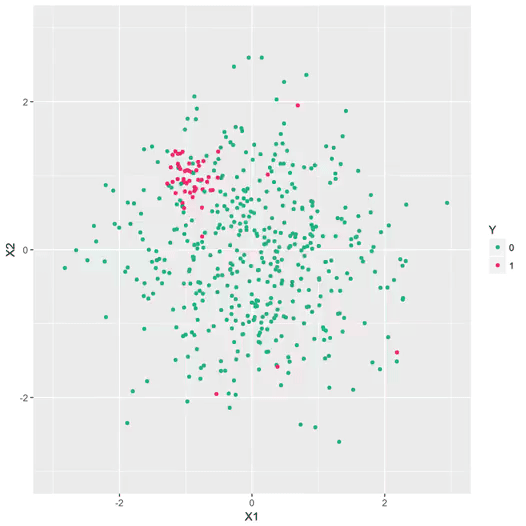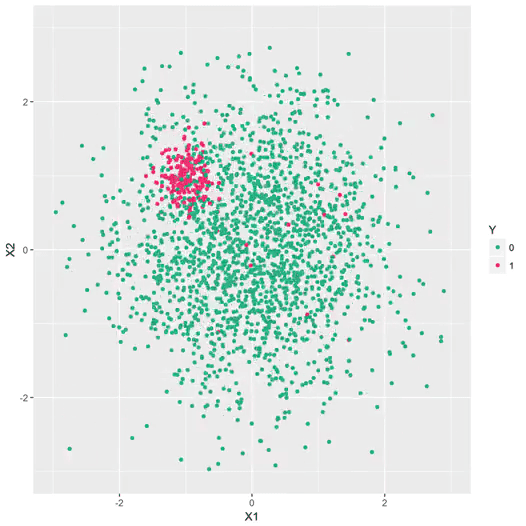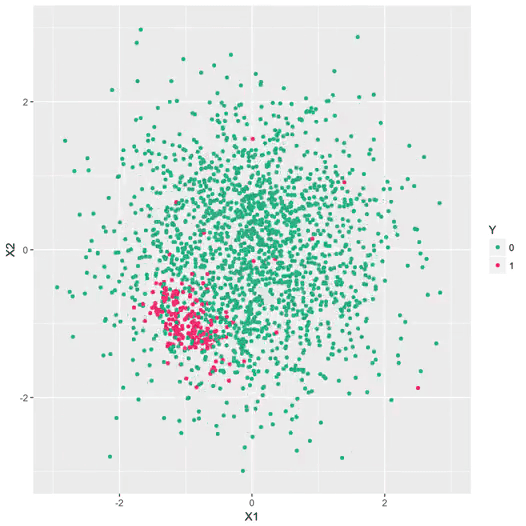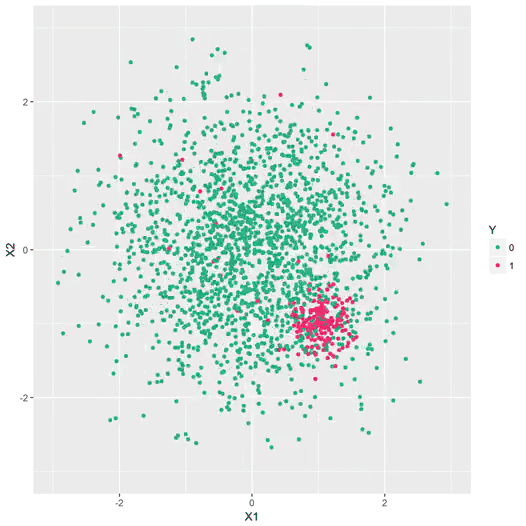
Figure 2 – Exemple de données qui dérivent. Ici, on représente schématiquement une problème bi-dimensionnel. Chaque point représente une transaction, et les fraudes sont indiquées en rouge. La dynamique des fraudeurs les oblige à explorer de nouvelles stratégies de manière dynamique. Un modèle qui a appris à distinguer la cible rouge/vert à un instant t devient rapidement obsolète.

Effondrement des modèles statiques

Pour illustrer cette obsolescence des modèles, on se propose de résoudre le problème de classification de la Figure 2 de trois manières différentes :

• Méthode 1 : on considère le jeu de données d’un bloc. On entraîne et évalue un modèle kNN (k-Nearest Neighbours) par validation croisée. C’est la méthode statique.
• Méthode 2 : on considère le jeu de données comme un flux. A chaque instant, le kNN s’entraîne sur tout l’historique passé, et prédit la prochaine observation. C’est la méthode incrémentale.
• Méthode 3 : on considère le jeu de données comme un flux. A chaque instant, le kNN s’entraîne sur un historique récent (10 000 observations) et prédit la prochaine observation. C’est la méthode fenêtre glissante.

En comparant les prédictions et les vrais labels au cours du temps, on obtient les courbes de performances décrites dans la Figure 3. On voit que le modèle incrémental tend vers un modèle statique (c’est l’effet persistance rétinienne infinie, ou catastrophic forgetting), tandis que le modèle fenêtre glissante réussit à maintenir sa performance à un niveau raisonnable.

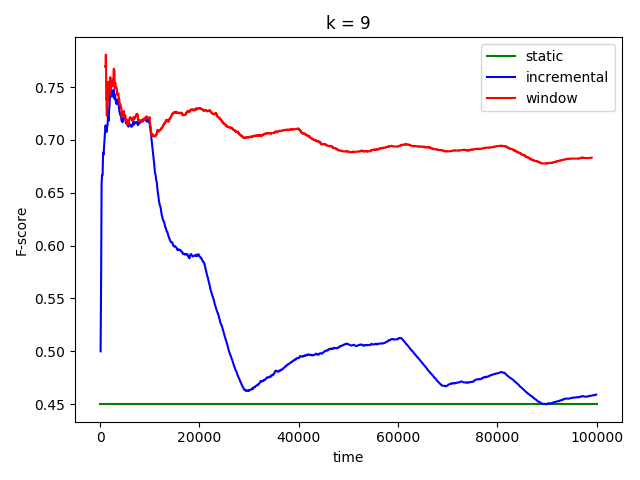
Figure 3 – Comparaison des performances (F-score) sur le toy dataset de la figure 2. La méthode 1 est représentée en vert : on considère le jeu de données comme un bloc et on évalue un kNN par validation croisée. En bleu, c’est la méthode 2: on considère le jeu de données comme une flux, mais pour chaque prédiction du kNN, on entraîne sur l’historique passé complet. Enfin en rouge, on représente la méthode 2 : on entraîne un kNN sur une fenêtre glissante de taille fixe et on prédit la prochaine observation.

Comment construire un algorithme adaptatif ?

On observe donc une forte valeur ajoutée à considérer l’évolution temporelle de la donnée dans un modèle prédictif en production. L’apprentissage adaptatif  (adaptive learning) regroupe l’ensemble des algorithmes de machine learning capables de s’adapter automatiquement à la dérive des données [2]. Il sont essentiellement constitués de trois briques élémentaires :

• un détecteur de dérive
• un modèle incrémental
• une stratégie ensembliste de combinaison des deux items précédents

Première brique élémentaire : comment détecter une dérive ?

La fenêtre glissante évoquée plus haut est une démarche passive : le modèle s’adaptera à son historique récent qu’il y ait ou qu’il n’y ait pas de raison de le faire. De plus, le ré-entraînement sur fenêtre glissante est très coûteux en temps de calcul. En effet, une variation infime du jeu de données déclenche un ré-entraînement complet du modèle. Une stratégie plus efficace consiste à ne s’adapter que lorsque c’est vraiment nécessaire et à accumuler la donnée tant qu’elle ne dérive pas. Pour ce faire, on fait appel à un détecteur de dérive.

Prenons l’exemple du détecteur ADWIN (Adaptive Windowing) [3], illustré sur la Figure 4. ADWIN va suspecter qu’une dérive a pu avoir lieu à tout moment, mettons t’, dans le passé. Pour le vérifier, il isole le passé et le futur de t’ en deux sous-fenêtre disjointes W_L (Window Left) et W_R (Window Right, voir Figure 5). Le détecteur effectue ensuite un test d’homogénéité basé sur la borne de Hoeffing pour décréter si oui ou non les deux sous-fenêtres sont significativement différentes. Si oui, alors une dérive est détectée, et se voit assigner la date t’. C’est ensuite à l’utilisateur (ou à l’algorithme) de prendre en compte ce signal pour  s’adapter, en ré-entraînant un modèle sur l’historique post-dérive par exemple. L’efficacité de l’algorithme résulte dans sa rapidité à explorer les t’ possibles.

Figure 4 – Fonctionnement de ADWIN. A chaque instant t, on suspecte qu’une dérive a eu lieu à un instant t’ < t. Pour le vérifier, on effectue un test d’homogénéité entre le passé et le futur de t’. Si une différence significative est détectée, alors on supprime la sous-fenêtre gauche. Pour être exhaustif, il faut sonder tous les t’ possibles, mais il existe des astuces (la compression exponentielle d’histogrammes) qui permettent d’agir en temps logarithmique.

Figure 5 – Pseudo-code de l’algorithme ADWIN. La fonction significant_difference est simplement un test statistique d’homogénéité basé sur la borne de Hoeffding.

Deuxième brique élémentaire : comment apprendre en continu sur un flux de données ?

Pour détecter une dérive le plus rapidement possible, il faut acquérir de l’information le plus rapidement possible, idéalement en temps réel. C’est le cas des flux de données. Nombre d’algorithmes classiques peuvent s’entraîner de manière incrémentale, notamment par descente de gradient. Toutefois, en présence de dérives sur un flux de données, trois éléments sont à prendre en compte :

• il est impossible d’anticiper quelle variable aura des valeurs manquantes,
• l’échelle de variation des variables peut changer drastiquement au cours du temps,
• la structure de corrélation du jeu de données évolue sans cesse.

Ces trois contraintes mises bout à bout jouent grandement en faveur des arbres des décisions : ils sont robustes aux valeurs manquantes, ils sont également invariants par transformation affine, et enfin leurs performances sont faiblement impactées par les corrélations fortes entre variables.

L’archétype de l’arbre de décision incrémental s’appelle l’arbre de Hoeffding [4]. Comme son nom l’indique (et comme ADWIN), il se base, sur la borne du même nom. La croissance de l’arbre se fait par optimisation gloutonne (greedy) (voir Figure 6) : au fur et à mesure que l’information s’accumule dans les feuilles, l’algorithme cherche une découpe optimale qui assure un gain d’entropie statistiquement significatif.

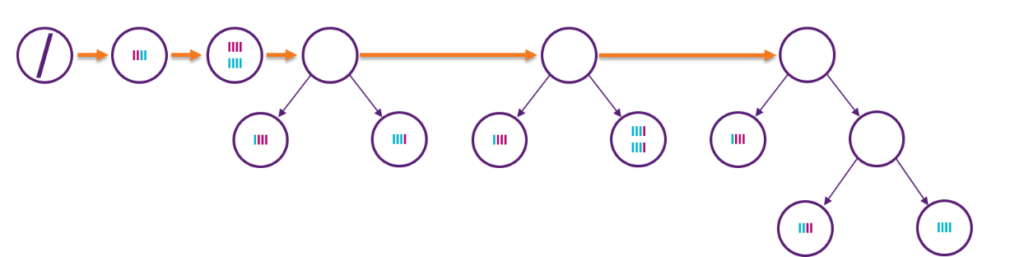
Figure 6 – Illustration de la croissance d’un arbre de Hoeffding. L’arbre commence son apprentissage avec un seul noeud et aucune observations à sa disposition. Au fur et à mesure que les données s’accumulent dans un noeud, l’algorithme cherche une découpe statistiquement avantageuse au sens de Hoeffding. Si une telle découpe existe, le noeud est découpé et les feuilles sous-jacentes vont accumuler de la donnée, et ainsi de suite.

Comme tout algorithme incrémental, l’arbre de Hoeffding est à mémoire infinie et est donc sujet au catastrophic forgetting (syndrôme de la persistence rétinienne infinie). C’est seulement une fois combiné avec un détecteur de dérive qu’on obtient un algorithme dit adaptatif.

Troisième brique élémentaire : comment concevoir une stratégie d’adaptation ?

La stratégie d’adaptation la plus populaire consiste à utiliser un ensemble dynamiques d’arbres de Hoeffding, interagissant au gré des détections de dérives fournies par ADWIN. L’idée est en fait celle d’un comité d’experts dynamique, où plusieurs modèles entraînés sur des périodes différentes votent avec une pondération indexée sur la performance courante. L’état de l’art de ce genre de stratégie est la forêt aléatoire adaptative (adaptive random forest) [5], dont le principe est le suivant.

Tout d’abord, chaque arbre individuel doit être différent de ses pairs car c’est dans la diversité des modèles que se crée la valeur de l’ensemble. Pour créer de la diversité entre les arbres, on fait appel aux techniques d’online bagging (voir Figure 7) [6], qui consistent à perturber aléatoirement le flux de données expérimenté par chaque arbre. On peut pousser plus loin la perturbation avec du feature sampling (tirage au sort des variables considérées pour chaque découpe).

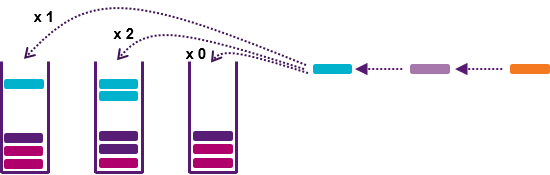
Figure 7 – Principe de l’online bagging. Pour chaque observation, on tire un nombre entier au hasard selon une loi de Poisson. Le résultat indique le nombre de duplicatas à distribuer à l’arbre. La loi de Poisson est utilisée car elle est équivalente à un échantillonnage bootstrap classique quand la taille du flux tend vers l’infini.

À ce point de l’explication, nous avons donc un ensemble diversifié d’arbres incrémentaux. La brique adaptative réside dans le détecteur de dérive ADWIN. En effet, chaque arbre voit ses performances mesurées en continu, et est muni de deux détecteurs (voir Figure 8). Le premier détecteur possède un seuil de détection faible et sert à notifier l’arbre qu’il rentre potentiellement dans une zone de turbulence (phase 1). Pour anticiper un futur remplacement de l’arbre, on plante alors un arbre alternatif (un bébé arbre). Le deuxième détecteur possède un seuil de détection élevé et sert à confirmer le premier. Si une telle confirmation a lieu (phase 2), l’arbre sénile est éjecté de l’ensemble et remplacé par son homologue juvénile (arbre devenu adolescent, et donc performant, depuis) planté en phase 1.

Figure 8 – Principe d’une forêt aléatoire adaptative. Chaque arbre est surveillé par un détecteur. Dès qu’un arbre observe une chute de performance douteuse, on lui met un avertissement (phase 1) et on démarre la croissance d’un arbre alternatif qui pourra prendre sa place. Si la chute de performance se confirme (phase 2), l’arbre juvénile évince et remplace son aîné, et se voit à sont tour surveillé par un détecteur de dérive à deux niveaux.

À ce stade, on a donc créé un éco-système algorithmique, où les arbres meurent, naissent et se succèdent de manière automatique sur la base des dérives de performance détectées par ADWIN. C’est à proprement parler un système d’intelligence artificielle, puisque le système s’adapte et se réentraîne de manière autonome et continue.

Quel est l’impact d’un modèle adaptatif sur la détection de fraude ?

Le problème de la vitesse de labellisation

Armé d’un modèle adaptatif tel la forêt aléatoire adaptative, on peut s’attaquer à un problème dynamique telle la détection de fraude sur les transactions bancaires. Or, à l’instar des modèles classiques d’apprentissage supervisé, le modèle a besoin d’un carburant, qui n’est autre que le flux de labels {transaction saine/transaction frauduleuse}. La vitesse d’adaptation de l’algorithme est donc directement pilotée par la vitesse de ce flux de label [7].

En réalité, on a donc deux échelles de temps antagonistes :

• la vitesse d’évolution de la fraude
• la vitesse de labellisation de la banque

Si la banque met plusieurs mois à labelliser les transactions, l’algorithme mettra autant de temps à s’adapter. D’ordinaire, la labellisation est un processus complexe, dont l’échelle de temps varie de quelques heures à quelques mois selon les transactions effectuées.

Impact du processus de labellisation sur la performance

Afin de mesurer l’impact de la vitesse de labellisation sur les performances de l’algorithme adaptatif, nous avons simulé plusieurs cas possibles :

• Cas idéal : la labellisation est instantanée et l’algorithme peut s’entraîner sur toutes les observations passées pour prédire l’observation courante et prendre une décision (bloquer la transaction par exemple).
• Investigations rapides : la labellisation ne s’effectue que sur la base des alertes du système de règles de la banque (moins de 1% du volume total), et avec un délai court, typiquement quelques heures. Ce scénario est celui où la banque a fait le choix, par exemple, de notifier par SMS ses clients dès qu’elle bloque une transaction, lesquels peuvent alors confirmer ou infirmer la fraude (labellisation).
• Investigations lentes: la labellisation ne s’effectue que sur la base des alertes du système de règles de la banque (moins de 1% du volume total), et avec un délai long, typiquement quelques jours. C’est le temps moyen de labellisation observé sur les alertes. Comme pour l’item précédent, on labellise les transactions non-alertées comme saines après une période de prescription de 60 jours.

Chaque jour, la banque possède un certain budget d’investigations, limité par le nombre d’experts sécurité qu’elle emploie. Chaque expert sécurité réalise un certain nombre d’investigations par jour, certaines aboutissant à des fraudes déjouées et d’autres à des gênes clients. L’objectif est de maximiser la proportion de fraude déjouées parmi les transactions investiguées par les experts sécurité. C’est donc une thématique de priorisation quotidienne.

Sur la Figure 9, on illustre comment notre modèle adaptatif influence l’efficacité de cette priorisation quotidienne, en faisant varier la vitesse de labellisation du système. On remarque notamment que :

• L’algorithme adaptatif nécessite un temps d’échauffement pendant lequel il commence à accumuler de la donnée et à améliorer sa performance. C’est attendu pour un algorithme incrémental.
• Plus la labellisation est rapide, plus l’algorithme adaptatif voit sa performance augmenter, c’est bien le signe d’une dynamique temporelle des données.
• Le cas investigations rapides est le plus prometteur : la performance du modèle est nettement supérieur au système en place, mais nécessite un investissement de la banque en terme d’envoi automatique de SMS à ses clients en cas de suspicion de fraude.

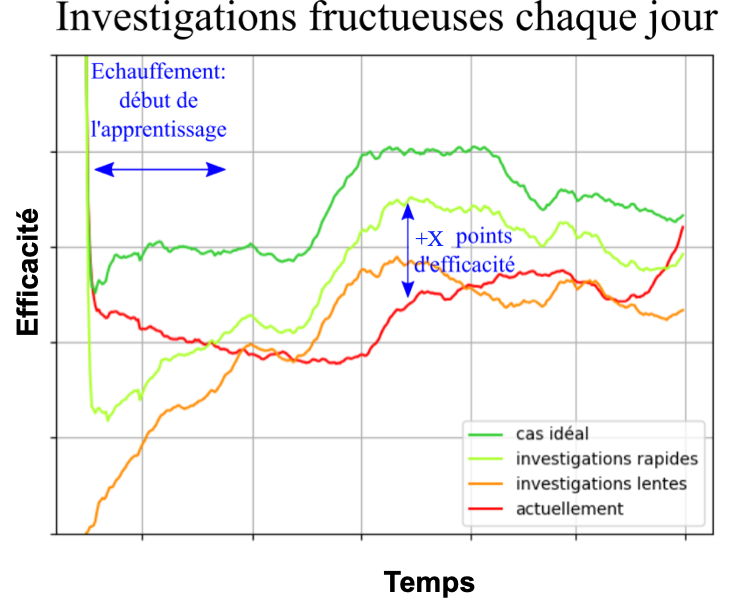
Figure 9 – Performances d’une forêt aléatoire adaptative pour prédire des fraudes sur un flux de transactions bancaires. Ici, on représente la proportion de fraudes avérées dans le top quotidien des transactions à risque. On représente les trois scénarios simulés par des couleurs différentes. La courbe en vert foncé représente le cas idéal. En vert clair, c’est le cas de la labellisation rapide des alertes (quelques heures) par envoi d’un SMS. La labellisation lente quant à elle (quelques jours), est représentée en orange. Finalement, en rouge, c’est le système de détection manuel pré-existant. Le graphe a été censuré pour des raisons de confidentialité.

À ce stade, on peut donc affirmer que les données de fraudes ont bel et bien une dynamique temporelle, et que l’algorithme adaptatif a su s’y adapter pour améliorer la performance de détection. Toutefois, cette étude ne permet pas d’évaluer complètement l’interaction de l’algorithme avec la boucle de rétro-action de la banque (Figure 1). Comme pour la plupart des modèles qui perturbent leurs environnements, seule une phase d’A/B testing permettrait d’évaluer l’algorithme en conditions réelles.

Conclusion

Les questions que posent l’apprentissage adaptatif

Les dérive des modèles est un sujet peu abordé, voir complètement ignoré par les organisations en phase de POC (Proof of Concept), avec des conséquences dramatiques lors du passage en production. Pourtant, toutes les données dérivent dans le temps, à des vitesses plus ou moins élevées. Les algorithmes adaptatifs sont pourtant développés intensément dans la littérature depuis une décennie, et sont implémentés en accès libre dans les bibliothèques en accès libre telles MOA, Apache-SAMOA et scikit-multiflow, qui centralisent le savoir-faire en la matière.

A n’en pas douter, ces algorithmes forment des leviers d’action puissants pour une mise en production. Toutefois, on peut également leur trouver quelques limites. Par exemple, le système de détection de dérive et d’adaptation automatique peut sembler opaque à l’utilisateur métier, et suscite un enjeu fort d’intelligibilité de la détection. L’avantage des arbres de décision incrémentaux est qu’ils bénéficient des mêmes atouts que leurs homologues classiques en terme d’intelligibilité. On peut notamment en extraire des règles logiques parlantes pour le métier.

Une deuxième limitation des algorithmes adaptatifs est qu’ils restent supervisés : ils sont d’autant plus performants qu’ils sont nourris avec de l’information labellisée fraîche et en abondance. Or, une telle information n’est pas toujours disponible à un coût raisonnable.

L’adaptation dans les organisations data

D’une manière plus générale, les mécanismes d’adaptation à la dérive des données dépendent de plusieurs facteurs propres à chaque entreprise : quelle est la fréquence de mise à jour des données ? des labels ? des modèles ? Quelle est la volumétrie des mises à jours ? Combien de modèles doivent être maintenus en conditions opérationnelles ? Chaque question trace un chemin dans une chaîne de décision et les techniques d’adaptation doivent (le comble !) s’adapter à chaque fois. En l’occurence, les algorithmes dits adaptatifs sont pensés principalement pour l’apprentissage en temps réel sur des flux de données denses et rapides. Plus généralement, ils offrent formalisent un cadre de réflexion autour du problème plus large du cycle de vie des modèles en production. Leur combinaison avec des technologies de cycle de vie des modèles telles MLFlow semble tracer le chemin vers l’état de l’art en la matière.

Références

[1] João Gama, Indre ̇ Žliobaite ̇, Albert Bifet, Mykola Pechenizkiy, and Abdelhamid Bouchachia. A survey on concept drift adaptation. ACM Comput. Surv., 46(4):44:1–44:37, March 2014

[2] Bartosz Krawczyk, Leandro L. Minku, Joo Gama, Jerzy Stefanowski, and Micha Woniak. Ensemble learning for data stream analysis

[3] Albert Bifet and Ricard Gavaldà. Kalman filters and adaptive windows for learning in data streams. In Proceedings of the 9th International Conference on Discovery Science, DS’06, pages 29–40, Berlin, Heidelberg, 2006. Springer-Verlag.

[4] Pedro Domingos and Geoff Hulten. Mining high-speed data streams. In Proceed- ings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’00, pages 71–80, New York, NY, USA, 2000. ACM.

[5] Heitor M. Gomes, Albert Bifet, Jesse Read, Jean Paul Barddal, Fabrício En- embreck, Bernhard Pfharinger, Geoff Holmes, and Talel Abdessalem. Adap- tive random forests for evolving data stream classification. Machine Learning, 106(9):1469–1495, Oct 2017.

[6] Nikunj C. Oza and Stuart Russell. Online bagging and boosting. In In Artificial Intelligence and Statistics 2001, pages 105–112. Morgan Kaufmann, 2001.

[7] A. Dal Pozzolo, G. Boracchi, O. Caelen, C. Alippi and G. Bontempi. Credit Card Fraud Detection: a Realistic Modeling and a Novel Learning Strategy. In IEEE Transactions on Neural Networks and Learning Systems (TNNLS), 2017.

✍Article écrit par Grégoire Martinon