Améliorer la qualité des données de prédiction par la méthode « Robust Principal Component Analysis » - cas Transilien SNCF
[latexpage]
Le développement des modèles d’apprentissage statistique a été très rapide ces dernières années. Un large choix de modèles est aujourd’hui disponible, et leur performance ne cesse de s’améliorer (Random Forest, XGBoost, LightGBM, modèles de Deep Learning…). Mais quelle que soit la performance de ces modèles, les données sont nécessaires à leur entraînement, et leur performance dépend crucialement de la quantité mais aussi de la qualité de ces données.
La qualité des données est donc un enjeu majeur pour l’apprentissage statistique. Les mesures peuvent être soumises à de nombreux types de corruptions : lacunes, bruit, anomalies ponctuelles ou collectives. Ces anomalies sont généralement dues à une défaillance du système de mesure ou à une perturbation réelle mais rare. Dans tous ces cas, il faut repérer et traiter ces valeurs exceptionnelles.
Nous avons utilisé la méthode « Robust Principal Component Analysis » (RPCA), avec plusieurs de ses variantes, dans le cadre de notre projet R&D AIfluence , en partenariat avec la SNCF et le Centre Borelli de l’ENS Paris-Saclay. Elle a permis d’améliorer la qualité des jeux de données de comptage de validations et de montées à bord des rames des voyageurs, et a ainsi permis d’améliorer la performance des modèles de prédictions. Nous vous la présentons ici.
Un exemple en séries temporelles : l’affluence sur le réseau Transilien de la SNCF
Nombre de validations par jour aux portiques de la gare Saint-Lazare, entre 2015 et 2019 (en open data).
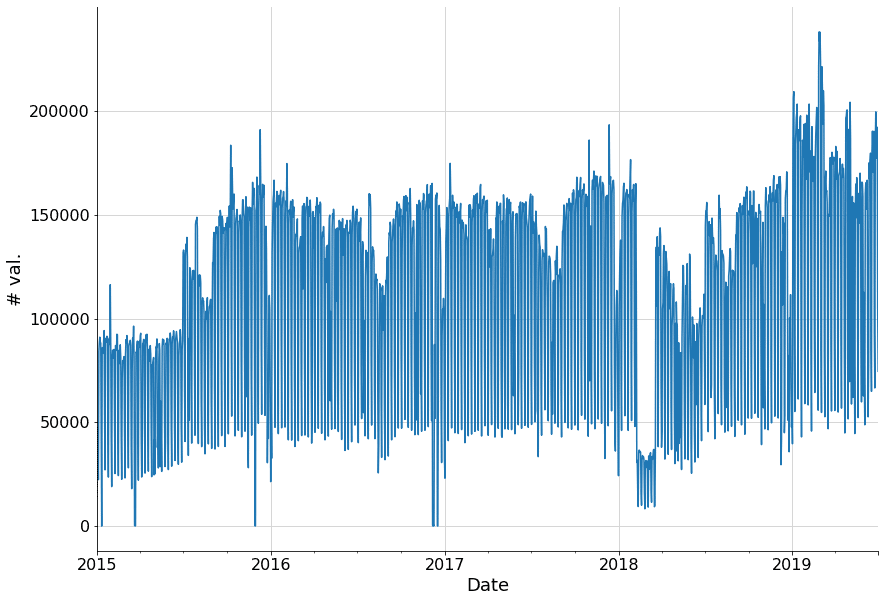
Nous pouvons constater la présence de données anormales au début de l’année 2018. Aussi, à plusieurs reprises, le nombre de validations est nul. Il pourrait s’agir d’un défaut du système de mesure, qui n’a compté aucun passager ce jour-là car il était désactivé. Il convient d’automatiser la détection de ces anomalies, d’évaluer leur effet sur un modèle d’apprentissage statistique et de les corriger, si nécessaire.
Plusieurs méthodes sont couramment utilisées pour détecter les anomalies. Par exemple, des méthodes statistiques consistant à considérer comme anormale une valeur qui s’écarte de la moyenne des données de plusieurs fois leur écart-type, avec la moyenne et l’écart-type éventuellement estimés sur des fenêtres glissantes en cas d’évolution temporelle (méthode dite du « z-score »). Pour être plus robuste aux anomalies, on peut remplacer la moyenne par la médiane et l’écart-type par la median absolute deviation. D’autres méthodes plus complexes existent comme les isolation forests fondées sur des arbres de décision (voir par exemple [1]).
La suppression des anomalies créé des trous dans les données, qui peuvent s’ajouter à des trous déjà existants. Pour l’imputation, de nombreuses méthodes existent, comme l’imputation par la moyenne, la médiane ou encore des méthodes itératives telles que MICE.
Dans cet article, on aborde une méthode fondée sur une technique de réduction de la dimension, l’Analyse en Composantes Principales ou PCA (Principal Components Analysis). Et surtout sa version robuste aux anomalies, dite Robust PCA.
Analyse en Composantes Principales (PCA)
Parmi les problématiques en science des données se trouve la « malédiction de la dimension ». On peut la résumer ainsi : la quantité de données nécessaire pour approcher une fonction croît exponentiellement avec la dimension de l’espace. Autrement dit, plus la dimension est grande, plus il faut de données pour remplir l’espace.
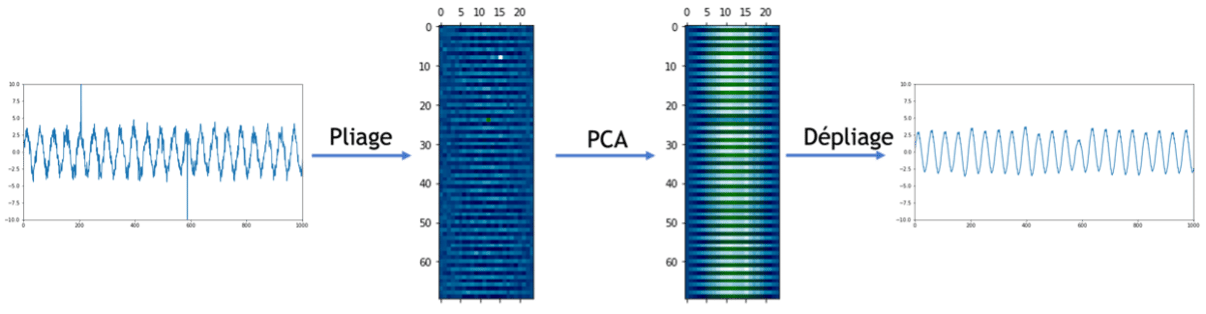
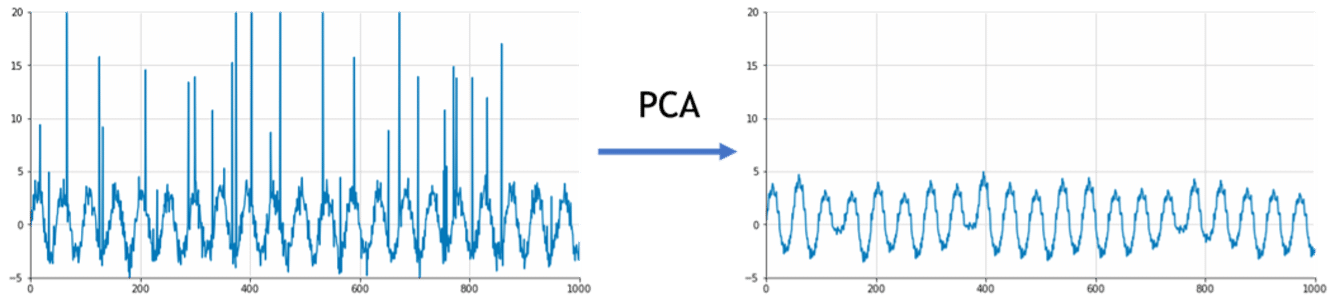
Une technique pour pallier ce problème consiste à réduire la dimension grâce à la PCA. Cette méthode suppose que la majeure partie de l’information des données est contenue dans un sous-espace de dimension inférieure à celui de l’espace entier, et à projeter les données sur cet espace. Cette projection correspond à l’information pertinente, corrigée, et la différence entre les données initiales et leur projection est interprétée comme un bruit, ou permet de détecter des anomalies (pour aller plus loin, voir par exemple [2]). Dans le cas d’un jeu de données 2D, la PCA identifie bien le sous-espace pertinent et l’unique anomalie: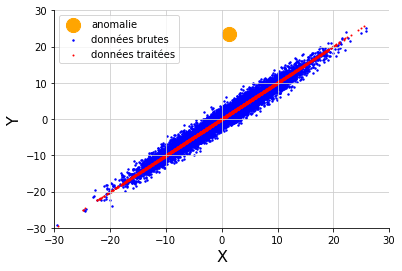
Pour appliquer cette méthode aux séries temporelles univariées, on peut plonger les observations correspondantes dans un espace de plusieurs dimensions afin d’exploiter la saisonnalité du signal. Par exemple, si l’on a une série avec une périodicité hebdomadaire, avec une valeur par heure, on peut ordonner les données dans une matrice avec 7 x 24 = 148 colonnes, chaque ligne correspondant à une semaine. Puis lui appliquer la méthode PCA avec un espace de dimension inférieure à 148. Enfin on déplie la matrice projetée ainsi obtenue pour revenir à une série univariée. Dans le cas d’une une sinusoïde bruitée comportant deux anomalies, la PCA permet bien de corriger les anomalies :
La méthode PCA a plusieurs limites. Notamment elle ne fonctionne pas avec des données manquantes. Il faut donc commencer par imputer avec une autre méthode. Ensuite, elle n’est pas robuste aux anomalies qu’elle est censée détecter, car les anomalies ont tendance à attirer le sous-espace de projection vers elles :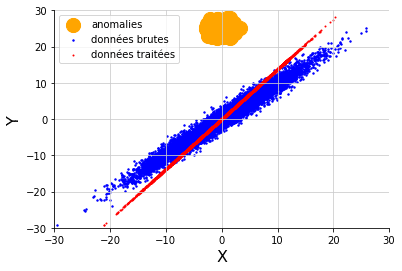
Cette sensibilité aux anomalies nuit à la reconstruction du signal, c’est pourquoi une variante plus robuste de la PCA est nécessaire. Par exemple, si l’on augmente significativement le nombre d’anomalies, la sinusoïde lissée par la méthode PCA semble tirée vers le haut :
La méthode « Robust PCA » ou RPCA
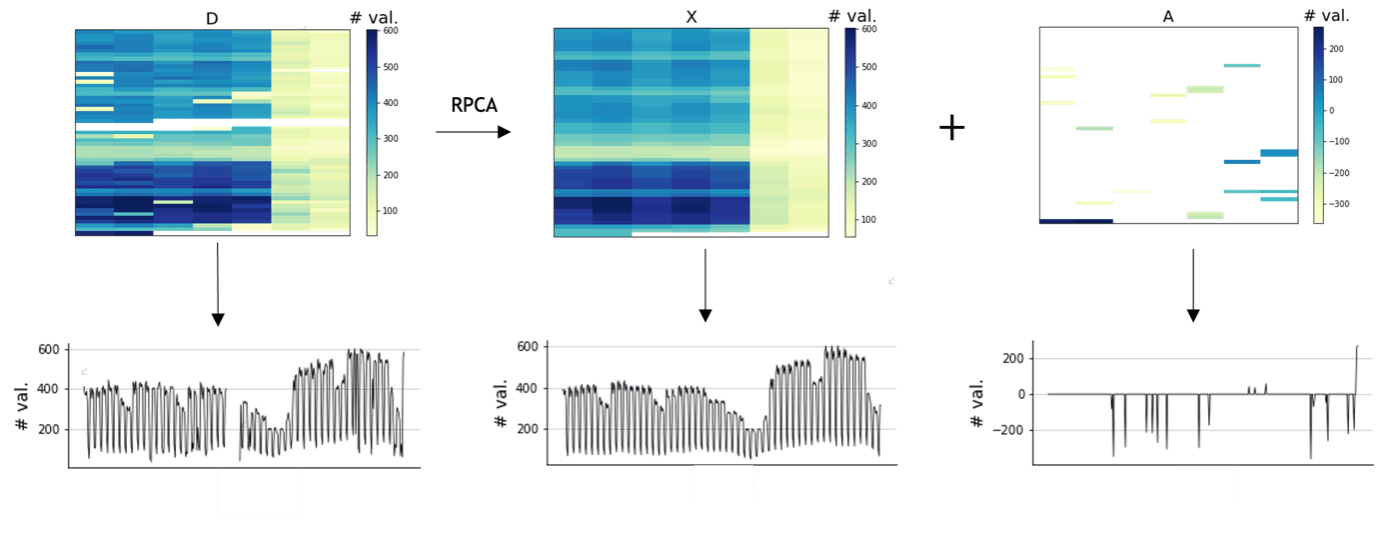
La méthode RPCA est une variante de la méthode PCA plus robuste aux anomalies. De plus, elle gère nativement les données manquantes, et elle les impute directement. La méthode RPCA repose sur le problème de minimisation où l’on cherche à décomposer la matrice d’observations D en une somme d’une matrice de rang faible X et d’une matrice creuse A (avec peu de valeurs non nulles) :
$$ min_{X, A} rang(X) + \lambda ||A||_0 \textrm{ t.q. }D = X + A $$
où $||A||_0$ est le nombre d’anomalies détectées. Plus précisément, la matrice X représente un signal régulier, qui correspond aux données projetées sur le sous-espace de dimension réduite et la matrice A correspond aux anomalies, qui sont rares mais potentiellement de forte intensité. Comme ce problème de minimisation est non-convexe, on résout à la place sa relaxation convexe :
$$ min_{X, A} ||X||_* + \lambda ||A||_1 \textrm{ t.q. }D = X + A $$
où $||X||_* $ est la norme nucléaire de $X$ et $||A||_1 = \sum_{i,j}|A_{i,j} |$.
Cette méthode est beaucoup plus robuste aux anomalies, et permet d’utiliser des jeux de données incomplets, qu’elle permet d’imputer directement. Reprenons l’exemple de la sinusoïde avec beaucoup d’anomalies.
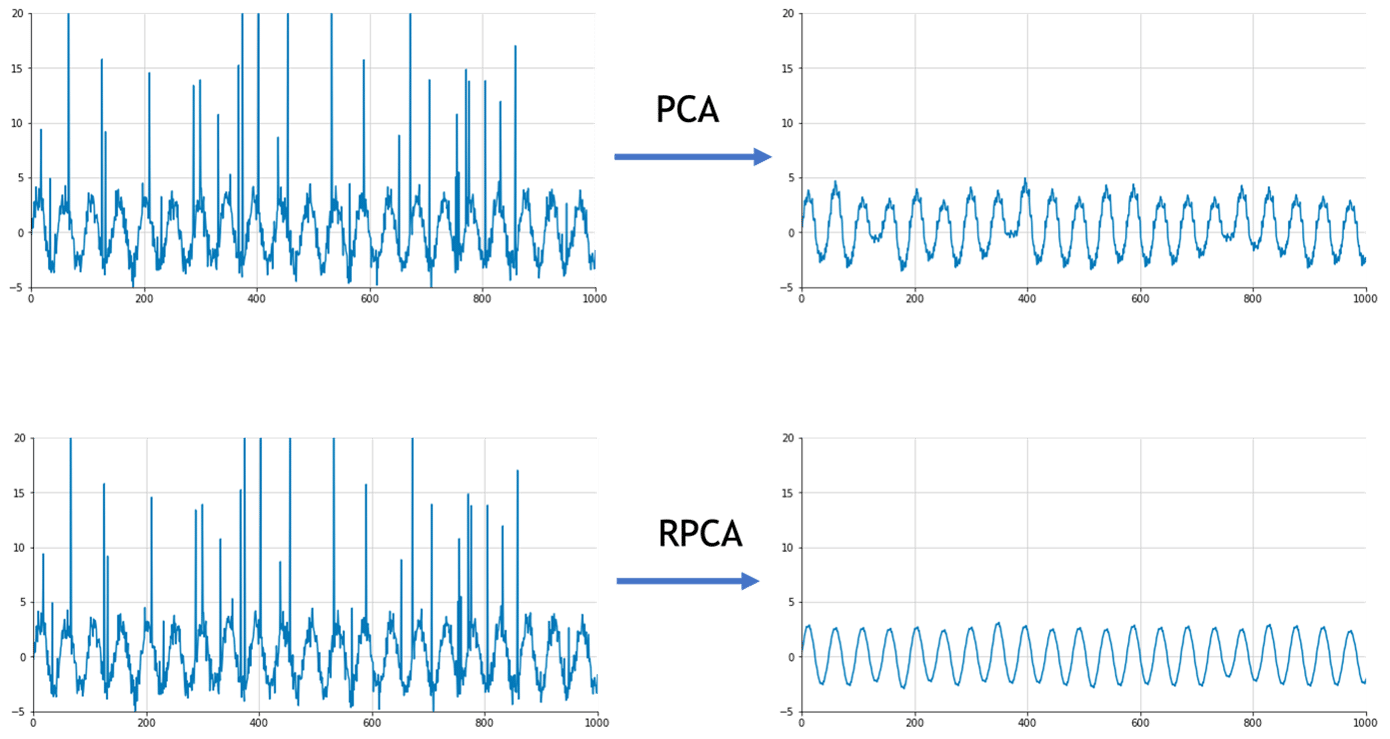
C’est une méthode paramétrique qui nécessite de déterminer le paramètre . Pour cela, on peut utiliser une validation croisée, en créant de fausses données manquantes ou de fausses anomalies, puis en sélectionnant la valeur permettant d’optimiser la qualité de la reconstruction. Si est grand, la norme de la matrice A sera beaucoup plus pénalisée et par conséquent la matrice A sera pratiquement vide, i.e. peu de valeurs seront considérées comme des anomalies. La matrice X sera très proche de D, donc a priori bruitée. À l’inverse, si est petit, la matrice X sera très régulière, et moins semblable à D, et A contiendra beaucoup d’anomalies. Il faut donc trouver le bon équilibre.
Revenons à l’exemple des comptages de validations . La méthode RPCA permet de reconstruire les données manquantes de manière cohérente, et est plus robuste aux anomalies. Pour aller plus loin, voir exemple [3].
[1] : Isolation Forests
[2] : The Elements of Statistical Learning: Data Mining, Inference, and Prediction, T. Hastie, R. Tibshirani, J. Friedman
[3] : Article à paraître, Robust PCA for Anomaly Detection and Data Imputation in Seasonal Time Series. HL Botterman, J. Roussel, T. Morzadec, A. Jabbari, N. Brunel
[4] : Open Data Transilien
Définir une stratégie data et mettre en place le plan opérationnel de transformation pour tirer le meilleur des données au service des enjeux et des objectifs business.
Data Scientist
Docteur en informatique des systèmes complexes, je m’intéresse à des problèmes de data science et suis enthousiaste pour appliquer de nouvelles techniques mathématiques sur des données expérimentales.
Data Scientist
Docteur en mathématiques fondamentales (géométrie riemannienne), je me suis tourné après mon cursus académique vers les data science, et plus particulièrement les séries temporelles. J’applique aujourd’hui cette compétence pour des problématiques de prévisions.
Data Scientist
Docteur en mathématiques appliquées à la physique statistiques, j’aborde aujourd’hui les problématiques de data science sous les angles scientifiques, techniques et métiers. J’ai un faible pour les modèles Bayésiens, les séries temporelles et l’IA de confiance !