Architecture des ordinateurs (2/2)

Cet article est le second d’une série de deux articles qui reprennent les grandes lignes d’une formation Quantmetry sur l’architecture des ordinateurs. Les biais de ma formation de physicien se feront sentir tout le long de l’article, vous êtes prévenus !

Par exemple, on peut considérer dans la figure ci-dessous que la conformation de l’eau savonneuse autour de deux anneaux correspond à une solution à énergie minimale d’une équation physique, et donc à un calcul puisque l’on peut mesurer la position de chaque point de la surface :

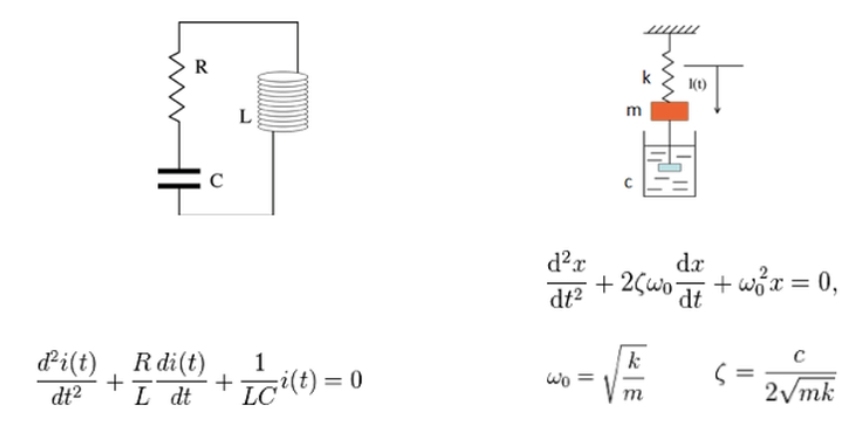
Autres exemples de calculs différentiels, la mesure de l’intensité ou de la position pour les systèmes électrique et mécanique ci-dessous, solution d’équations d’oscillations très classiques :

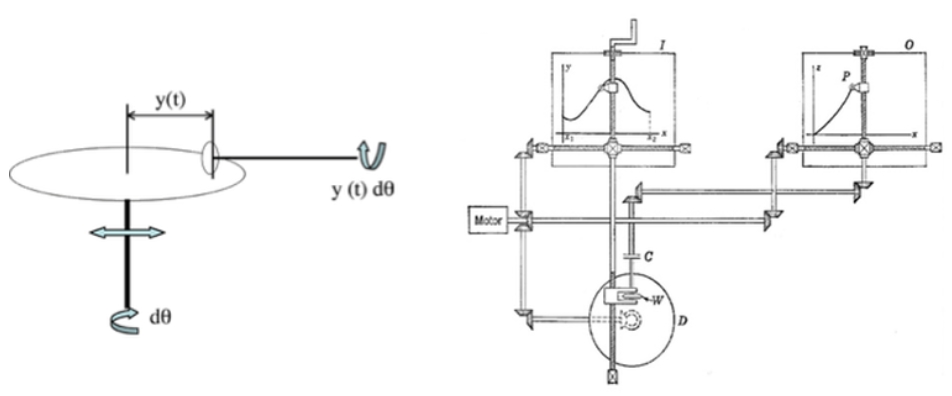
On peut également considérer des exemples d’intégrateurs analogiques, comme le système mécanique suivant :

On devine aisément qu’un calcul quantique correspond simplement à la mesure de l’état final d’un système microscopique évoluant sous des contraintes censées représenter le calcul à effectuer.

Ainsi, nous avons répondu aux trois premières questions que l’on se posait au début du premier article, à savoir :

1. Comment l’information est-elle manipulée au sein d’un ordinateur ?

2. Quel sens précis donner au terme « calculer » dans l’expression « un ordinateur effectue des calculs » ?

3. Comment comprendre la notion de calcul quand on parle d’ordinateurs analogiques ou quantiques ?

Nous avions conclu le premier article en évoquant la notion de machine de Turing et son rôle essentiel pour comparer la puissance de calcul de machines différentes. Les questions qui restaient en suspens vont nous permettre de structurer la présentation de ce concept et son apport en théorie de la calculabilité :

1. Comment s’articule la théorie des machines de Turing avec les notions de calcul et d’architecture digitale ?

2. À quel niveau se fait l’abstraction entre la couche physique et la couche logicielle dans un ordinateur ?

3. L’architecture issue des machines de Turing est-elle la seule possible ? La meilleure ? Les ordinateurs analogiques ou quantiques peuvent-ils calculer des choses que nos ordinateurs digitaux ne peuvent pas calculer ?

Calcul physique et calcul symbolique

La notion d’algorithme

Nous avons vu précédemment qu’un même calcul abstrait pouvait être effectué grâce à des machines physiquement très différentes. Nous avons nommé les transformations d’états de ces machines « calculs physiques ». Si l’on cherche à définir plus rigoureusement la notion de calcul abstrait, on est rapidement amené à s’intéresser à la notion de manipulation symbolique, et donc à celle d’algorithme.

Un algorithme est défini comme étant une procédure non-ambiguë et finie permettant de produire la réponse à une question. En voici quelques exemples :

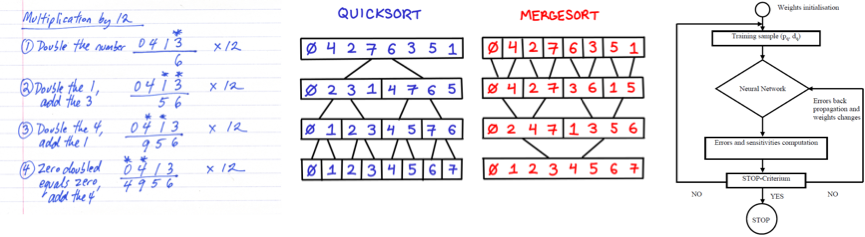
Cette définition est censée englober tout ce qu’un humain peut calculer à l’aide d’une feuille et d’un crayon, sans contrainte de temps ni de ressources. Elle constitue une abstraction de tous les calculs que l’on cherche à implémenter dans des systèmes physiques. Reste à définir maintenant un modèle à la jonction de ces deux mondes pour justifier la pertinence de cette abstraction et pouvoir comparer les machines entre elles.

La machine de Turing

La machine de Turing est une machine abstraite consistant en :

• Une bande infinie composée de cellules contenant des symboles d’un alphabet fini, par exemple {0, 1, A, X, #}.

• Une tête de lecture/écriture sur la bande qui peut se déplacer une cellule à la fois, à droite ou à gauche. La cellule pointée par la tête est surlignée en jaune.

• Un registre d’états qui enregistre les états de la machine de Turing. Parmi ces états se trouve un état « Start » associé à l’initialisation de la machine de Turing.

• Une table finie d’instructions qui pour un état donné de la machine de Turing et un symbole lu sur la cellule pointée par la tête donne une instruction non-ambiguë à la machine.

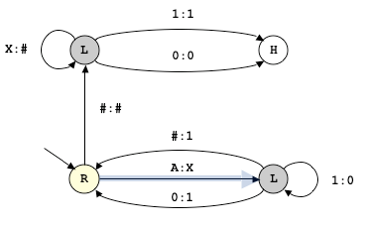
Il s’agit donc essentiellement d’une généralisation de la notion familière d’automate. La force du concept de machine de Turing est de modéliser à la fois les manipulations symboliques et des machines physiques évoluant selon un schéma causal bien défini, opérant ainsi une jonction entre les notions de calcul symbolique ou algorithme et celle de calcul physique.

Analysons maintenant en détail l’exemple de la machine de Turing donné en définition. La machine représentée compte le nombre de A, enregistre ce nombre sous forme binaire à gauche de la séquence de A, et transforme cette séquence en une séquence de #. Voici le résultat des deux premières instructions :

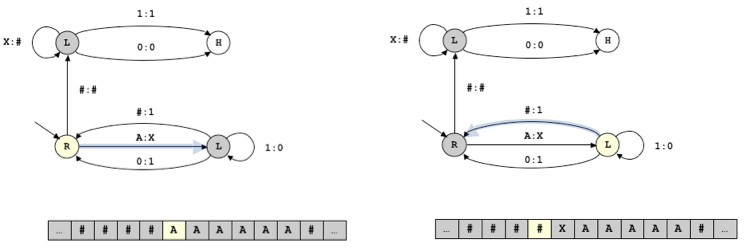
Et voici les transformations de la bande après quelques itérations :

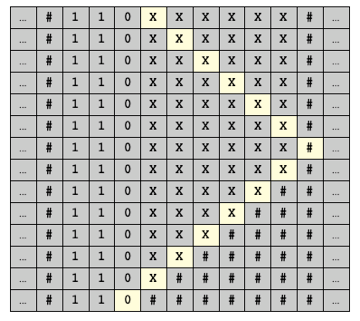
 On peut ainsi imaginer des machines de Turing pour tout type d’algorithme : addition binaire, multiplication par 24, etc. Une question naturelle vient alors à l’esprit : faut-il nécessairement des jeux d’instructions complexes pour effectuer des calculs complexes ? La réponse, illustrée de manière spectaculaire à travers la notion de machine de Turing universelle, est non !

Machine de Turing universelle

Considérons l’instruction suivante :

SUBLEQ = soustraire et bifurquer si négatif

Plus précisément, on soustrait le contenu d’une adresse ‘b’ du contenu d’une adresse ‘a’, on stocke le résultat dans l’adresse ‘b’ et, si le résultat est négatif, on se déplace à l’adresse ‘c’, sinon on passe à l’instruction suivante. En pseudocode cela donne :

                                   subleq a, b, c : Mem[b] = Mem[b] – Mem[a] ;

                                                              if (Mem[b] ≤ 0) goto c

Malgré sa simplicité, on peut démontrer qu’il s’agit bien là d’une instruction universelle, i.e. d’une instruction capable de reproduire n’importe quelle autre instruction si répétée selon un schéma précis, que l’on nomme programme. L’addition peut par exemple être reproduite par des soustractions sans bifurcation comme suit :

                                   ADD a, b = subleq a, Z ; subleq Z, b ; subleq Z, Z

La première instruction stock dans Z la valeur de la différence entre a et Z (de valeur initiale 0), à savoir -a, la seconde stock dans b la différence entre b et -a, à savoir b+a, enfin la dernière instruction réinitialise la valeur de Z à 0.

Cette instruction est ce que l’on appelle une instruction universelle : c’est une instruction capable de simuler n’importe quelle machine de Turing. Elle est donc capable d’exécuter tout algorithme ! À noter que pour passer du pseudocode de cette instruction au formalisme des machines de Turing (qui n’intègre pas de notion de déplacement à une adresse quelconque), cette dernière doit être légèrement étoffée, mais le nouveau jeu d’instructions restera relativement simple malgré son pouvoir de calcul universel. La simulation d’une autre machine de Turing sera alors faite via des programmes représentant des patterns des instructions de base stockés sur une bande. On parlera alors de machine de Turing universelle.

Nous voyons ainsi que le concept de machine de Turing permet de comparer entre elles les capacités théoriques de calculs de machines physiques exécutant des algorithmes via des instructions, ces instructions étant associées à des transformations causales d’états. Certaines machines sont incomparables, d’autres le sont via la relation de simulation, avec notamment certaines machines qui sont universelles. C’est bien cette classe de machines de Turing universelles qui est à la base de l’architecture moderne des ordinateurs.

De la machine de Turing à l’architecture digitale

Réalisation physique

En mappant les transitions entre états de la machine de Turing sur des transitions entre états d’un système physique, on peut représenter tout algorithme par un calcul physique. Le jeu d’instructions de la machine de Turing caractérisera alors tous les calculs que peut effectuer la machine physique. L’architecture de Von Neumann, représentée ci-dessous et qui est le standard d’architecture des ordinateurs numériques modernes, a été introduite par le mathématicien John Von Neumann comme mise en pratique des travaux de Turing :

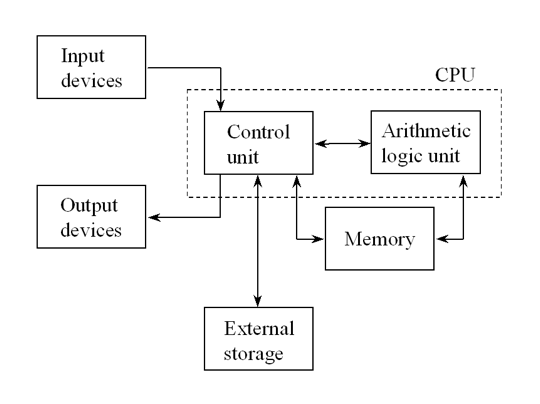
Un processeur est composé d’une unité arithmétique et logique, d’une unité de contrôle et d’une horloge interne. L’unité de contrôle comporte des mémoires spécifiques à l’accès en lecture/écriture très rapide et dénommées « registres » ou « mémoire cache ». Ces mémoires permettent le stockage des valeurs intermédiaires lors des calculs. Le processeur communique avec :

• une mémoire qui, couplée au processeur, implémente la notion de registre d’états et une partie finie de la bande mémoire,

• une mémoire externe qui joue le rôle de bande (potentiellement) infinie,

• des périphériques qui peuvent modifier les informations contenues dans la bande mémoire.

Nous allons maintenant étudier plus en détail chacun des composants de cette architecture.

L’unité arithmétique et logique

Il s’agit du coeur du système, celui dans lequel le jeu d’instructions est physiquement encodé. Toute instruction pouvant être représentée par un ensemble de portes logiques, les unités logiques modernes correspondent essentiellement à une architecture complexe de portes connectées entre elles. Voici un exemple d’unité logique exécutant 8 types d’opérations différentes sur deux objets encodés en 8 bits :

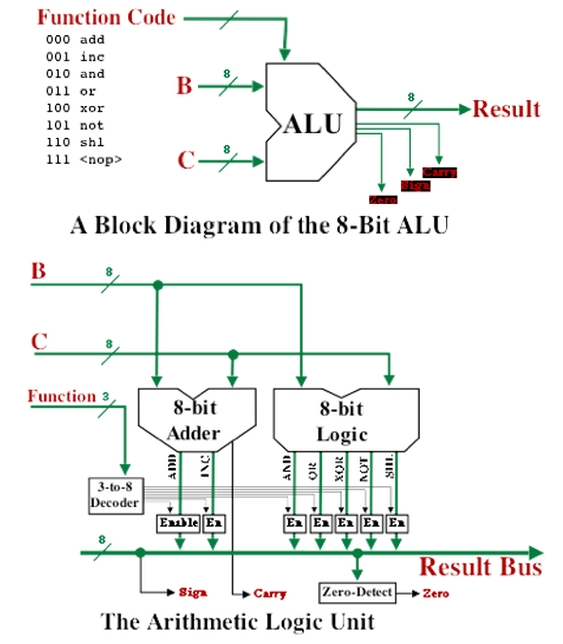
Le schéma ci-dessus correspond à un système composé de portes logiques électroniques, mais nous avons déjà vu dans le premier article qu’une porte logique pouvait être réalisée de manière mécanique. L’avantage d’une porte logique électronique est la possibilité de miniaturisation des contrôles qu’offrent les transistors.

Les transistors

Il existe plusieurs sortes de transistors, nous allons ici nous concentrer sur la forme la plus commune dans les ordinateurs, dite transistor MOSFET pour « Metal Oxyde Semi-conductor Field Effect Transistor ». Le transistor MOSFET est une sorte d’interrupteur qui permet de contrôler le transfert des électrons d’un point S (source) à un point D (drain) de manière contrôlée via une tension appliquée au point G (grille). En voici un schéma simplifié, ainsi que la courbe de courant entre D et S en fonction de la tension entre D et S et entre G et S :

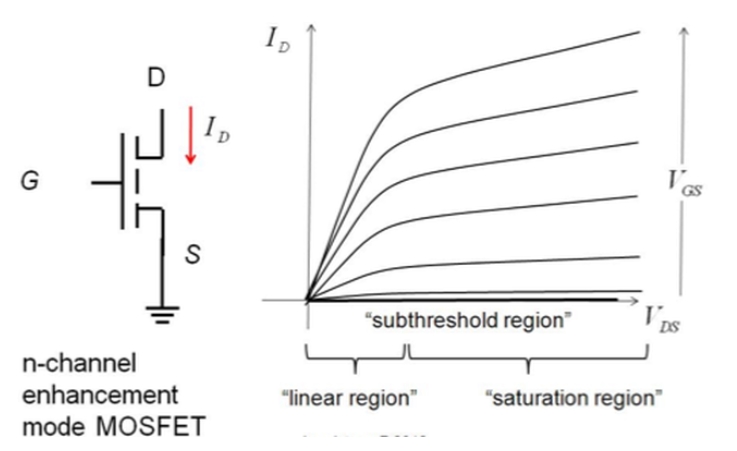
En-deça d’une tension GS seuil, le transistor possède une résistance infinie. Une fois cette tension de seuil franchie, il existe pour les faibles tensions DS un régime de résistance linéaire typique des résistants ohmiques, la courbe devenant non linéaire au fur et à mesure de l’augmentation de la tension DS. L’utilisation du transistor en régime dit de saturation permet de définir la notion de bit : 0 si aucun courant ne circule entre D et S, 1 sinon, avec une modulation via la tension GS.

Ce comportement est directement lié au caractère semi-conducteur du matériau composant le transistor. Les semi-conducteurs désignent des matériaux dont la conductivité électrique est intermédiaire entre métaux et isolants. Cette conductivité peut être contrôlée par dopage : en utilisant des impuretés, on peut produire soit un excès d’électrons (semi-conducteur de type N) soit un excès de trous (semi-conducteur de type P). En mettant en contact des semi-conducteurs dopés différemment, un échange à la frontière s’établit : des électrons passent vers le type P, tandis que des trous passent vers le type N. Les matériaux étant neutres initialement, cette diffusion va engendrer un champ électrique à la jonction de sens opposé au déplacement des trous, ce qui permet d’atteindre un équilibre (dont les solutions exactes sont déterminées grâce à la physique quantique) avec une zone dite de déplétion chargée électriquement et dépourvue de porteurs libres :

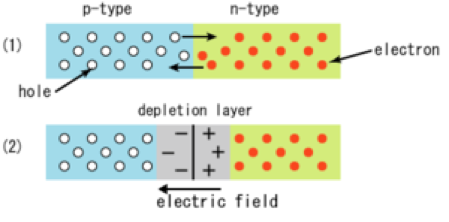
Seule l’application d’une tension de sens opposée au champ électrique et de valeur supérieure permet à des électrons de circuler du type p vers le type n. Les électrons peuvent par contre circuler librement depuis le type n vers le type p pour toute valeur de tension. Cette propriété est à la base de fonctionnement des transistors. Voici le schéma détaillé d’un transistor MOSFET :

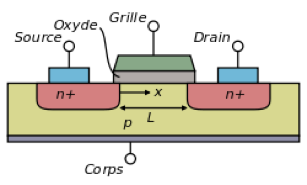
Les jonctions p-n et n-p constituent des barrières de potentiel, empêchant le courant de circuler entre drain et source. Si l’on applique une tension sur la grille, les trous de la partie de type p au contact de l’oxyde vont être repoussés vers le bas, tandis que les électrons vont remonter vers le haut, inversant ainsi le type de semi-conducteur au contact de l’oxyde en type n. Au-delà d’une tension seuil, des électrons vont pouvoir circuler entre la source et le drain via le tunnel de type n ainsi créé. Plus la tension de grille est élevée, plus le tunnel de type n s’épaissit, plus le courant entre D et S augmente. En appliquant une tension positive sur le drain, le déplacement vertical des trous et des électrons dans cette zone est moins important car la différence de potentiel entre grille et substrat de type p diminue, ce qui aboutit au pincement du tunnel de circulation et à un épaissisement de la zone de déplétion autour du drain :

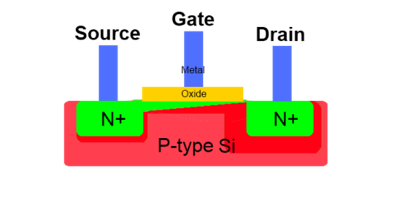
La tension dans la zone à laquelle le pincement se produit est par définition la tension seuil. La taille du trajet entre la source et le pincement définit alors la vitesse initiale des électrons qui entrent dans la zone de déplétion commune à la source, au canal de circulation et au drain : à tension GS constante, la vitesse des électrons diminue avec le décalage vers la gauche du pincement, c’est-à-dire avec l’augmentation de la tension DS, d’où une pente d’intensité qui diminue également. Ces différents éléments expliquent la forme de la courbe de courant DS en fonction des tensions DS et GS.

Les circuits intégrés

Au départ, on utilisait des transistors d’une taille de quelques millimètres en les connectant grâce à des fils de cuivre pour constuire les portes logiques. La logique est toujours la même aujourd’hui, mais miniaturisée par plusieurs facteurs : on est passé de transistors de quelques microns dans les années 70 à quelques nanomètres (une centaines d’atomes) dans les années 2010 !

Pour pouvoir construire des circuits à base de transistors à cette échelle, on utilise des techniques de gravures chimique et laser sur des plaques de semi-conducteurs, la principale technique mise en oeuvre étant la photolithographie. En simplifiant les choses, le processus démarre par la création par fusion d’un lingot de silicium pur à 99.9999999% à partir de la silice composant le sable, forme naturelle du dioxyde de silicium. Ce lingot de silicium pur est ensuite découpé en disques dénommés « wafers », polis jusqu’à l’obtention d’une finition miroir. Le fabriquant applique ensuite un liquide photorésistant similaire à ceux utilisés pour les pellicules en photographie argentique (bleu sur l’image). Un mouvement circulaire est imprimé aux wafers afin d’optimiser la répartition du liquide à la surface. Le traitement photorésistant est ensuite exposé à de la lumière ultraviolette (UV) via des masques, ce qui a pour effet de rendre la partie complémentaire au masque sur le wafer soluble. La lentille utilisée permet une réduction linéaire par quatre du motif du masque. Le procédé est répété plusieurs fois afin de pouvoir superposer plusieurs couches à la solubilité différente. On applique ensuite un solvant, faisant ainsi ressortir l’architecture imprimée par applications successives des masques :

Plusieurs agents chimiques viennent parfaire les sillons creusés grâce aux rayons UV, avant de retirer puis ré-appliquer une couche de traitement photorésistant qui servira en combinaison avec les UV à délimiter les zones à doper via un faisceau d’ions :

Après l’implantation ionique, la deuxième couche de traitement photorésistant est retirée. On dépose ensuite une couche isolante (magenta sur l’image) sur laquelle on gravera des trous qui seront comblés par dépôt de cuivre, suivi d’un polissage :

En itérant le processus de dépôt et de polissage du cuivre, on est capable de créer un véritable réseau « d’autoroutes » pour les charges électriques. L’architecture de ce réseau est spécifique à chaque processeur et fait partie des secrets industriels des fabriquants :

L’étape des tests de fonctionnement permet ensuite de sélectionner les portions du wafer à garder après découpage en « dies ». Ces dies sont ensuite combinés à un substrat qui assure l’interface électrique et mécanique avec la carte mère, tandis que la protection en métal sert à diffuser la chaleur :

Les mémoires

Comprendre le fonctionnement d’une instruction fait intervenir l’unité arithmétique et logique mais également différents types de mémoire. Voici une hiérarchie des différents types de mémoires physiques que l’on peut trouver au sein d’un ordinateur :

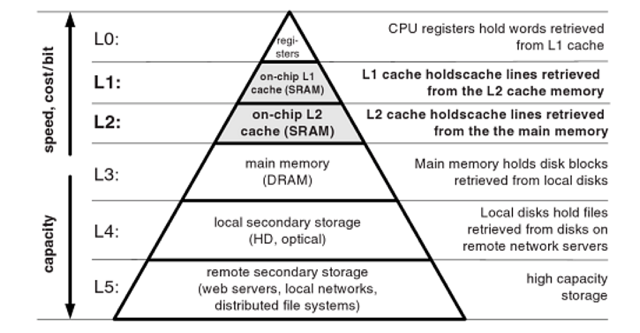
 On constate qu’il convient de distinguer trois grandes classes de mémoire :

• Les registres ou mémoire cache : très proches physiquement de l’unité logique et intégrés au processeur, ils sont associés aux opérations les plus récurrentes de celui-ci.  Il s’agit le plus souvent de mémoires dites SRAM pour Static Random Access Memory, composées de 4 à 6 transistors par cellule qui permettent de maintenir un bit d’information en mémoire sous forme de charge électrique sans besoin de rafraichissement. Ces cellules ne peuvent être référencées individuellement, c’est leur regroupement en byte qui l’est. Le schéma d’une cellule SRAM (leur fabrication utilise des techniques similaires à celle des dies) est le suivant :

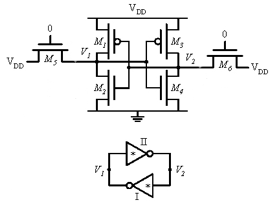
• La RAM : ces mémoires sont utilisées pour comme endroit de stockage des instructions à exécuter dans le cadre d’un programme. Elles sont le plus souvent de type DRAM pour Dynamic RAM. Chaque cellule est constituée d’un condensateur couplé à un transistor et nécessite d’être rafaîchie en permanence pour maintenir l’information stockée sous forme de charge électrique, ce qui explique le fait que ce type de mémoire se vide une fois l’ordinateur éteint :

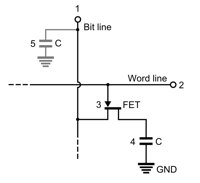
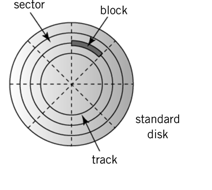
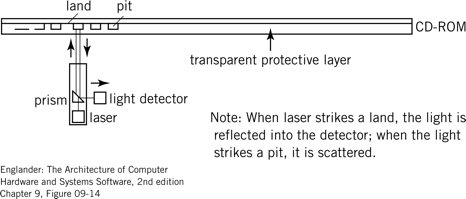
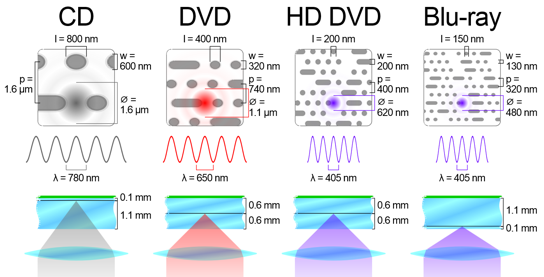
• Mémoire externe : il s’agit d’une mémoire lente qui joue le rôle de bande mémoire potentiellement infinie. Elle sert essentiellement à stocker de manière froide les programmes. Le plus souvent, elle est implémentée sous forme de disque optique et nécessite une interface Input/Output (I/O) dédiée pour communiquer avec le processeur. Un triplet secteur – bloc – piste permet de définir une zone de lecture/écriture. L’information dans cette zone est stockée sous forme de creux et de plateaux : lorsque le laser de la tête du disque tombe sur un plateau, le rayon est réfléchi vers le détecteur, sinon il est diffusé. Les déplacements de la tête sont unitaires, ce qui permet d’encoder de l’information : une succession de deux creux ou de deux plateaux correspond à 0, tandis qu’un changement plateau-creux ou creux-plateau correspond à 1. Plus la longueur d’onde du laser est courte, plus la taille des creux et plateaux que l’on peut distinguer est petite, plus la mémoire disponible sur une surface donnée est grande ! D’autres types de mémoire comme les SSD existent, nous nous contenterons de l’évoquer ici.

Le processeur

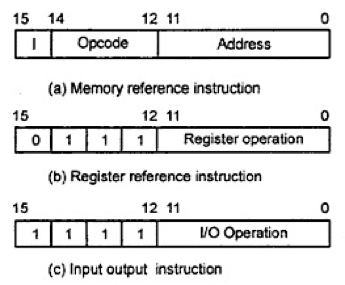
Les traitements d’information sont effectués au sein du processeur via des instructions. La notion d’instruction d’un processeur est un peu plus large que celle du formalisme de machine de Turing, puisqu’elle intègre non seulement l’opération à effectuer (dénommée « opcode » en anglais pour « operation code »), mais également l’adresse mémoire où l’on peut trouver les éléments sur lesquels effectuer des opérations. Un processeur est donc caractérisé par le jeu d’instructions qu’il peut exécuter ainsi que par le nombre d’adresses mémoire qu’ils peuvent référencer :2³² pour les processeurs 32 bits,  2⁶⁴ pour les processeurs 64 bits. Dans la réalité, un processeur dits 64 bits aura des instructions de taille 64 bits, et référencera donc moins que  adresses différentes, car une partie des bits de l’instruction seront dédiés à définir l’opcode. Dans les ordinateurs modernes, près de 46 bits seulement sont disponibles pour l’adressage mémoire, d’où des RAM d’une taille maximale de quelques To, contre 4Go pour les processeurs 32 bits. Voici un exemple d’instructions différentes pour un processeur 16 bits :

Le processeur exécute les instructions les unes après les autres (sauf saut commandé par une instruction particulière), à un rythme de plusieurs milliards d’instructions par seconde pour les processeurs modernes. Il s’agit d’un véritable ballet de charges électriques dans un circuit infiniment plus complexe que celui d’une porte logique à choix multiple, mais le principe de calcul reste le même : un schéma de charges électriques déclenche telle ou telle opération selon l’opcode représenté, tandis que les charges représentant l’adresse vont permettre, par une succession de phénomènes physiques, d’aller récupérer les opérandes – également stockés sous forme de charge – dans la plus petite unité référençable d’un registre ou de la RAM. Cette plus petite unité référençable contient par définition un byte d’information, ce qui correspond le plus souvent à un octet (8 bits) dans les mémoires modernes.

De manière générale, le jeu d’instructions définit les formats de données que traite le processeur, l’adressage des différents types de mémoire, les interruptions, les gestions d’exceptions et les I/O externes. Il s’agit du seul langage que l’ordinateur est capable d’exécuter directement. Sa dépendance à l’égard de la construction physique du processeur fait que chaque famille de processeurs possède son propre langage machine, avec parfois des compatibilités assurées entre différentes familles.

Quant à l’horologe interne du processeur, il s’agit d’un circuit dédié générant un signal qui impose à tous les circuits internes de l’ordinateur un rythme de transfert d’information régulier. Quand on a dit ça, on n’a pas encore dit grand chose, mais l’implémentation d’une horloge est un sujet complexe, et nous nous contenterons ici de cette description sommaire.

Le bus système

Le bus système est un ensemble de fils de cuivre connectant les différents composants de l’ordinateur, dont l’unité logique, les registres, la RAM, la mémoire et les périphériques externes. Il est composé de trois parties :

• Bus d’adresses

• Bus de données

• Bus de contrôle

Quand le processeur veut communiquer avec une mémoire ou un périphérique, il va spécifier un signal de contrôle qui sera transféré via le bus de contrôle (par exemple lire ou écrire sur la RAM), ainsi qu’une adresse mémoire spécifiée sur le bus dédié et précisant d’où rapatrier ou bien où écrire les données transportées via le bus de données.

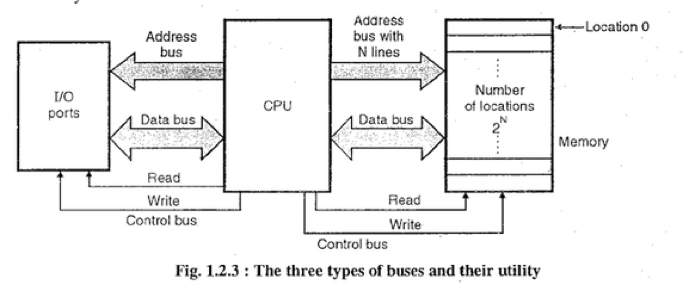
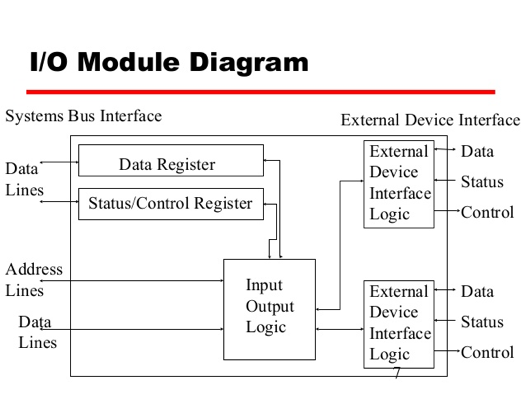
L’interface I/O

Comme le laisse entendre la notion de bus « système », un processeur s’adresse aux périphériques externes de la même manière qu’il communique avec la mémoire. Or ces périphériques collectent et manipulent le plus souvent des informations dans une forme initialement très éloignée de celle des instructions comprises par le processeur. Ces périphériques doivent donc exécuter en amont des opérations « intelligentes » de transformation de l’information dans un format approprié, et possèdent donc de vériables unités logiques dédiées dénommées modules I/O. Chaque interface I/O possède donc son propre module I/O qui assure la communication avec le CPU. Le détail du fonctionnement d’un module I/O nécessiterait un article à part entière, et nous nous contenterons donc ici du schéma global de fonctionnement décrit.

Le cycle Fetch-Decode-Execute

Maintenant que les notions de processeur, de mémoire, de bus système et d’interfaces I/O ont été présentées, nous allons nous intéresser au cycle d’opérations grâce auxquelles une succession d’instructions peut être traitée dans un processeur.  Ce cycle est connu en anglais sous le nom de « Fetch-Decode-Execute » pour « Récupérer-Décoder-Exécuter », et correspond au processus opérationnel le plus basique au sein d’un ordinateur.

Commençons par définir les différents composants du processeur intervenant dans ce cycle :

• Un registre dénommé compteur ordinal ou pointeur d’instruction (Program Counter) qui stock l’adresse de la prochaine instruction à exécuter.

• Un registre d’adresse mémoire (Memory Adress Register ou MAR) qui stocke une adresse mémoire où lire ou écrire.

• Un registre d’instruction stockant l’instruction en cours d’exécution.

• L’unité de contrôle qui décode l’instruction stockée dans le registre d’instruction et coordonne les opérations de récupération des données et l’activation d’une opération logique

• L’unité arithmétique et logique qui exécute l’opération spécifiée par l’instruction.

Le déroulement du cycle est le suivant :

• Démarrage : le cycle commence dès que l’ordinateur est branché sur du courant électrique. En simplifiant les choses, la valeur initiale du compteur ordinal est prédéfinie et correspond à une adresse spécifique dénommée « vecteur reset ». Cette adresse pointe sur une zone spécifique de la Read-Only Memory (ROM), une mémoire non-volatile où l’information est encodée en dur sur un circuit, par exemple une matrice de diodes ou de transistors. Cette zone de la ROM contient les instructions qui permettront d’initialiser la RAM et d’y charger un programme dénommé BIOS, dont le rôle est de vérifier le bon fonctionnement de tous les composants de l’ordinateur et de trouver un système d’exploitation à lancer. Ce processus est connu sous le nom de « booting ».

• Fetch : le processeur envoie le contenu du compteur ordinal dans la MAR et une commande de lecture sur le bus de contrôle. La RAM répond à la commande en envoyant l’instruction contenue dans l’adresse spécifiée via le bus de données. L’instruction est copiée du bus de données vers le registre d’instruction. À la fin de l’opération, le compteur ordinal pointe sur l’adresse de l’instruction suivante à exécuter via un simple incrément d’adresse ou bien une bifurcation.

• Decode : l’instruction est décodée et l’unité de contrôle coordonne les opérations de stockage dans différents registres de l’opcode ainsi que des opérandes le cas échéant. En effet, l’instruction peut ou non porter sur des opérandes déjà présents dans des registres. Dans ce dernier cas, l’unité de contrôle va récupérer les opérandes dans les adresses RAM indiquées dans l’instruction.

• Execute : l’unité de contrôle fait exécuter l’instruction décodée à l’unité arithmétique et logique, et coordonne les opérations pour stocker le résultat en registre ou RAM. Le cycle de lecture et écriture en RAM étant plus long que celui du processeur, l’exécution de l’instruction suivante peut commencer avant la fin de celui-ci.

Le schéma fonctionnel ci-dessous résume le cycle décrit :

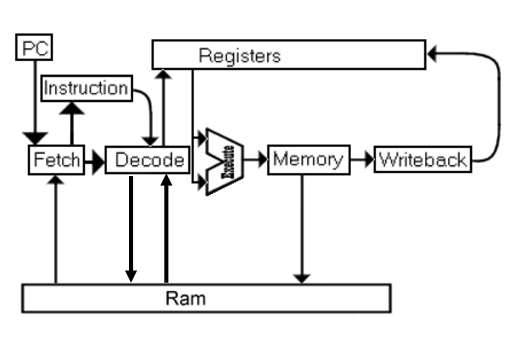
Il s’agit bien entendu d’un schéma très simplifié, chaque partie étant composée de circuits électroniques aux interactions complexes. Voici un exemple de diagramme fonctionnel plus détaillé d’un processeur :

 Auparavant, plusieurs cycles d’horloge étaient nécessaires pour exécuter une instruction, mais dans les ordinateurs d’aujourd’hui, des techniques de parallélisation et de prévision statistique des instructions suivantes permettent d’exécuter plusieurs instructions par cycle d’horloge.

Abstraction et langages de programmation

Comme vu dans la section précédente, le jeu d’instructions du processeur est le seul langage que l’ordinateur est capable d’exécuter directement. On peut programmer n’importe quel algorithme grâce aux jeux d’instructions des ordinateurs modernes car ces derniers sont Turing universels. Cependant, une telle pratique est extrêment complexe car pour écrire un programme il faut manipuler un système physique comme les cartes à perforer de façon à structurer bit par bit chacune des instructions à partir d’un pseudo-code proche du langage machine.

La première idée pour simplifier la programmation a donc été de créer des programmes nommés « assembleurs » capables de traduire des symboles mnémoniques, i.e. simples à retenir, en des instructions du code machine. Considérons par exemple  l’instruction « 10110000 01100001 » de la famille de processeurs x86 qui signifie « écrire le nombre 97 dans le registre AL ». Définissons une représentation symbolique de cette opération : « mov al, 97 ». En tapant sur le clavier la commande « mov al, 97 », et en simplifiant les choses, on peut dire que le module I/O du clavier va traduire ce texte en ASCII, chaque lettre ou espace étant alors representé par 8 bits, i.e. un byte, soit exactement la plus petite adresse référençable en mémoire. Imaginons maintenant que ce script soit enregistré en RAM dans 10 adresses précises de bytes. Écrire l’embryon d’un programme assembleur revient à programmer en code machine des instructions qui par une succession d’accès aux registres, à la RAM, et d’opérations de l’unité d’arithmétique et logique vont lire à un moment ou à un autre les 10 bytes associés à chaque lettre du script, et produire en sortie l’instruction « 10110000 01100001 » avant de l’exécuter. En complexifiant petit à petit notre programme assembleur jusqu’à représenter la plus petite sous-partie Turing complète du jeu d’instructions du processeur, on atteint l’étape dite « d’auto-hébergement » : toute nouvelle version du langage plus riche en instructions peut être écrite à partir de la version basique ayant permis d’atteindre l’auto-hébergement.

Cette idée de traiter un langage comme données d’un programme, très présente dans la théorie des machines de Turing à travers la notion de simulation, permet quelque chose de bien plus profond qu’une simplification symbolique. En effet, en considérant deux commandes telles que « mov al, 97 » et « mov bl, 68 », on constate qu’il existe une structure des instructions du processeur de la forme « mov, destination, source » qui n’est pas visible au niveau du code machine : c’est un premier exemple de la notion d’abstraction. Autre exemple, on peut définir des commandes du type « mov ax, [bx]+10 », qui signifie « stocker dans le registre ‘ax’ le contenu de l’adresse obtenue en ajoutant 10 au contenu du registre ‘bx' ».

En poursuivant cet effort d’abstraction, on atteint la notion de macro, un bloc de texte que l’on peut insérer dans un programme via une commande d’appel et un nom choisi par le programmeur. Nous avons déjà évoqué dans le premier article l’importance de cette simplification sémantique dans la compréhension de la notion d’abstraction. En effet, en faisant appel à des macros, le programmeur peut manipuler des nouveaux objets via des opérations nouvellement définies plus adaptés au problème qu’il cherche à résoudre. L’ontologie s’éloigne ainsi de la description physique des traitements que subit l’information, mais permet du même coup la création de programmes de moins en moins dépendants de l’architecture physique sur laquelle les calculs sont opérés. Bien entendu, cela se fait au prix d’un allongement du code machine à exécuter, mais l’augmentation des capacités de calculs des ordinateurs grâce à la miniaturisation, couplée à une augmentation de la productivité des programmeurs, et de la réutilisabilité du code, ont rendu possible tant d’un point  de vue technique qu’économique une véritable avalanche d’abstractions : des langages de haut niveau comme FORTRAN ou C sont créés, convertis en langage assembleur ou directement en langage machine grâce à des programmes nommés compilateurs ; ces mêmes langages de haut niveau ont été utilisés pour construire des programmes complexes commes les noyaux, parties essentielles des systèmes d’exploitation permettant une abstraction quasi-complète des composants matériels de l’ordinateur et la manipulation de formats abstraits de données. La liste des exemples serait trop longue, chacun méritant probablement un livre pour décrire tous les challenges relevés, les mauvaises pistes explorées et les succès rencontrés dans sa réalisation.

Nous avons ainsi répondu à la quatrième question : les machines de Turing constituent par définition le paradigme de l’architecture digitale, à la base des techniques modernes de construction des ordinateurs et des langages de programmation. La réponse à la question sur l’endroit où se fait l’abstraction entre la couche matérielle et la couche logicielle est plus complexe : il s’agit d’une abstraction progressive et par paliers. Cette abstraction commence par la loi I = f(V) non linéaire des transistors, qui permet, au-delà de la tension seuil, une définition stable de la notion de bit malgré les variations de la tension de grille. Elle se poursuit via des circuits électroniques de contrôle permettant de définir un jeu d’instructions commun à toute une famille de processeurs malgré des comportements jamais identiques des composants. Enfin, les programmes assembleurs, compilateurs et langages de haut niveau permettent, par des overheads de code accumulés, d’aboutir aux noyaux, où l’on peut considérer que la couche matérielle est complètement abstraite. Cet équilibre de conventions est extrêment fragile, comme on peut s’en rendre compte en déversant de l’eau sur un ordinateur !

Le bruit comme fondement de l’universalité des machines de Turing

Nous avons détaillé le fonctionnement des ordinateurs numériques en partant des machines de Turing. Fort bien ! Mais qu’est ce qui nous assure que ces machines calculent tout ce que l’on peut calculer ? En effet, la thèse de Church-Turing, qui déclare que « tout ce qui est calculable par un humain avec des ressources illimitées est calculable par une machine de Turing », est, comme son nom l’indique, une thèse, et non une démonstration. À l’origine de ce postulat se trouve l’équivalence démontrée entre trois modèles inventés indépendemment pour modéliser la notion d’algorithme : celui de la machine de Turing par Turing, celui du λ-calcul par Church, et enfin celui des fonctions récursives par Gödel.

Mais, objectera-t-on, je peux très bien imaginer un système analogique modélisé par une équation différentielle dont la variable est la température et dont la solution pour une condition intiale donnée est exactement un nombre réel, comme π, √2 ou la constante de Chaitin Ω, alors que les machines de Turing ne peuvent au mieux qu’approximer de tels nombres. Cela signifie-t-il qu’il existe des calculs que les machines de Turing ne peuvent effectuer ? La réponse, comme nous allons le voir, est non.

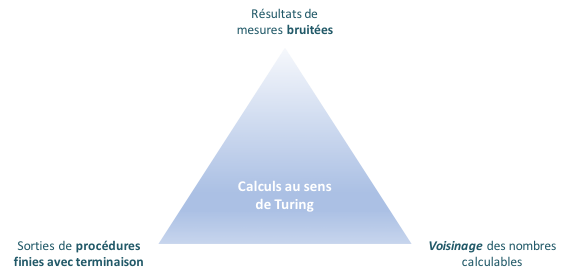
Commençons par distinguer entre deux types de nombres : les nombres réels dits calculables comme π ou √2, pour lesquels il existe une procédure d’approximation finie aussi précise que voulu, et les nombres dits incalculables comme la constante de Chaitin, généralement liés aux problèmes indécidables comme le problème d’arrêt.

Les nombres calculables sont donc par définition calculables au sens de Turing, et l’objection basée sur la notion d’appareil analogique ne résiste pas à une analyse plus approfondie : tout calcul physique se termine par la mesure de l’état final du système, or cette mesure, pour arbitrairement précise qu’elle soit, est toujours bruitée et ne peut donc déterminer une variable qu’avec un nombre fini de décimales. Les systèmes analogiques ne permettent donc pas de faire autre chose qu’approximer des nombres calculables. Le bruit évoqué trouve son origine dans la finitude des ressources en énergie et temps disponibles pour toute expérience concrète. L’objection basée sur des systèmes quantiques résiste tout aussi peu à l’analyse : le bruit empêche la manipulation d’un ensemble continu d’états quantiques, et l’on est donc ramené à un ensemble discret d’états dont l’évolution est décrite par de l’algèbre linéaire, et qui est donc simulable par un ordinateur classique.

Les nombres incalculables, quant à eux, ne peuvent être mesurés que comme sorties d’appareils non standards, comme les appareils impliquant la proximité avec un trou noir ou utilisant une superposition infinie d’états quantiques. Ces conditions, pour autant qu’elles permettent une violation de la thèse de Church-Turing, sont d’ordre essentiellement théorique et spéculatif, et relèvent du domaine de l’hypercalcul.

En conclusion, l’imbrication entre les notions de sortie d’algorithme et de mesure bruitée d’un système physique montre l’équivalence entre le calcul au sens de la thèse de Church-Turing et ce qui est calculable grâce à des appareils que l’homme peut construire, qu’ils soient classiques discrets, classiques analogiques ou quantiques. Nous avons ainsi obtenu une réponse à notre dernière question.

Qu’est-ce qui justifie donc l’engouement autour des ordinateurs quantiques ? Leur véritable nouveauté, c’est l’espace des états manipulés qui est de type vectoriel et qui permet, via les possibilités offertes de définir des états superposés, d’imaginer de nouvelles formes d’algorithmes. Ces algorithmes quantiques permettent de calculer plus vite les solutions à certains problèmes, comme l’algorithme de Shor qui permet de factoriser un nombre entier en temps polynomial, menaçant ainsi l’un des fondements de la cryptographie moderne. On peut même imaginer à terme que les capacités offertes par les ordinateurs quantiques puissent bouleverser l’état actuel de la théorie de la complexité, mais en aucun cas un ordinateur quantique ne permettra de calculer des choses nouvelles. L’architecture basée sur le modèle des machines de Turing est donc bien le paradigme ultime pour calculer ce qui est calculable !