Quant Blog Le blog des Experts Data & IA

Recherche et développement

16/12/2019

Classification et déséquilibre de classes

Temps de lecture : 9 minutes

La classification de données dont la distribution des modalités de la classe est très éloignée de la distribution uniforme (ou classes déséquilibrées), est une situation relativement fréquente dans certaines industries. Plus concrètement, les classes déséquilibrées font généralement référence à un problème de classification où les classes ne sont pas représentées de façon égale. Il y a des cas où un déséquilibre de classe n’est pas seulement commun, il est attendu. Par exemple, dans le cas de détection de transactions frauduleuses, il y a un déséquilibre. La grande majorité des transactions seront dans la classe « Non-Fraude » et une très petite minorité dans la classe « Fraude ».

Ce déséquilibre de classe augmente nettement la difficulté de l’apprentissage par l’algorithme de classification. En effet, l’algorithme n’a que peu d’exemples de la classe minoritaire sur lesquels apprendre. Il est donc biaisé vers la population des négatifs et produit des prédictions potentiellement moins robustes qu’en l’absence de déséquilibre.

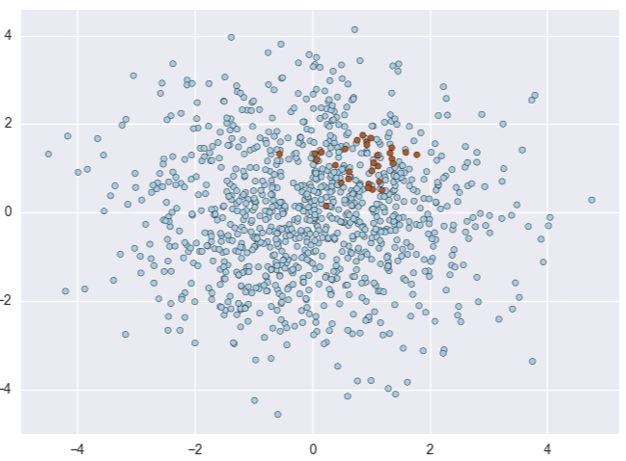
Cas de déséquilibre de classes, les points rouges représentant la classe minoritaire.

Métriques de performances

Métriques à seuil de décision : Accuracy vs others

Comment mesurer la performance de son algorithme dans ces situations ? Il faut dans un premier temps se méfier de l’exactitude (accuracy en anglais). Effectivement, dans le cas du déséquilibre de classes, l’exactitude peut être trompeuse. Avec un jeu de données de deux classes, où la première classe représente 90% des données, si le classifieur prédit que chaque exemple appartient à la première classe, l’exactitude sera de 90%, mais ce classifieur est inutile dans la pratique. D’autres métriques sont plus pertinentes dans le cas du déséquilibre de classes.

La précision pour minimiser le taux d’erreurs parmi les exemples prédits positifs par le modèle
Le rappel pour tenter de détecter un maximum de positif
Le F1-score pour trouver un compromis entre la précision et le rappel. Lorsqu’il est aussi coûteux de manquer un positif que de déclarer un faux positif

D’autres métriques sont très efficaces et informatives pour le data scientist mais moins interprétables que les précédentes. Parmi elles :

La métrique Kappa de Cohen est en général utilisée pour mesurer la performance du classifieur en la comparant à celle d’un classifieur aléatoire. Dans le cadre des classes déséquilibrées, on l’utilisera en comparant le modèle à système classant tous les exemples comme étant de la classe majoritaire
La courbe lift dans le cadre du ciblage marketing par exemple. Le lift est une mesure de l’efficacité d’un modèle prédictif calculée comme le rapport entre les performances obtenues avec et sans le modèle prédictif pour une proportion de cibles (choisies aléatoirement vs choisies par un algorithme de machine learning) contactées.
Le Brier Score est une mesure de calibration de la distribution des probabilités émises par l’algorithme. Elle est calculée en prenant l’erreur quadratique moyenne entre les probabilités émises par l’algorithme pour la classe observée et la classe en question.

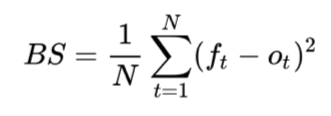
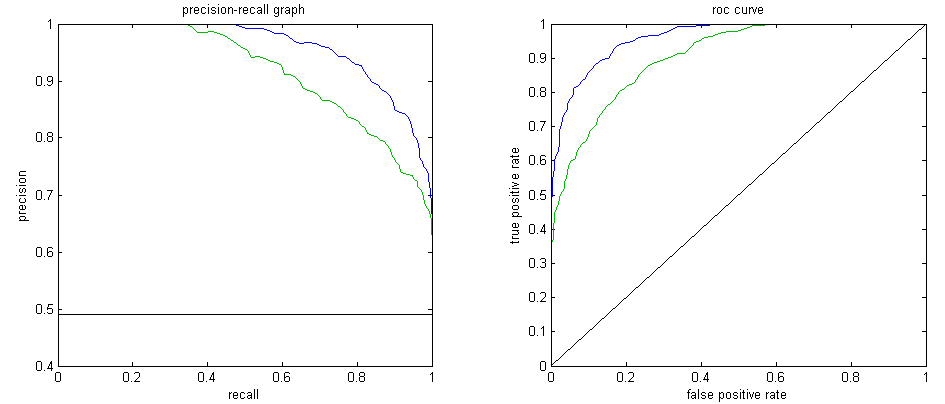
Les métriques model-wide : Courbe ROC vs Courbe Précision-Rappel

La courbe ROC est l’une des métriques model-wide ( testant l’algorithme pour plusieurs seuils de classification) les plus populaires. Toutefois dans le cadre du déséquilibre de classes, il faut privilégier la courbe Précision-Rappel. En effet la courbe ROC n’est pas sensible au taux de déséquilibre car le taux de faux positif, en abscisse de la courbe ROC, est stable quand le taux de négatif est lui élevé. De même, le taux de vrais positifs, en ordonnée de la courbe, ne prend pas en considération ce déséquilibre. La courbe Précision-Rappel intégrant la notion de déséquilibre, via la précision en abscisse et le rappel en ordonnée, est donc plus informative dans ce cadre. Dans un but d’évaluation de modèle non spécifique à un domaine d’utilisation, l’aire sous la courbe Précision-Rappel est la métrique à privilégier.

Processing de données : Le ré-échantillonnage dans le cadre du déséquilibre de classes.

Pour faire face à ce déséquilibre de classes, deux approches sont possibles. Il est possible d’adapter l’étape d’apprentissage à cette situation ou alors d’adapter l’étape de traitement des données du projet de data science. C’est cette seconde approche qui est étudiée la plus en profondeur dans cet article, via le ré-échantillonnage du jeu de données.

Undersampling

Le sous-échantillonnage (undersampling) consiste à rééquilibrer le jeu de données en diminuant le nombre d’instances de la classe majoritaire.

Random Undersampling

Le sous-échantillonnage aléatoire (Random Undersampling) consiste à tirer au hasard des échantillons de la classe majoritaire, avec ou sans remplacement. Toutefois elle peut accroître la variance du classifieur et peut éventuellement éliminer des échantillons utiles ou importants.

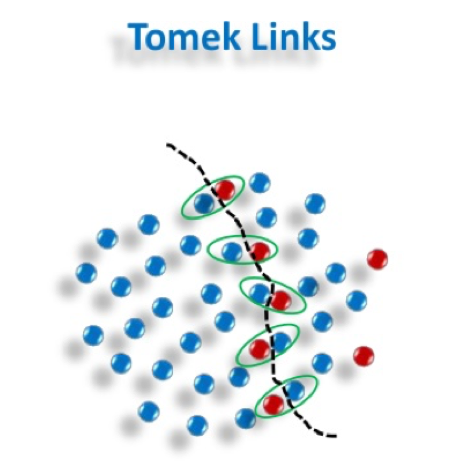
Tomek Links

Les liens de Tomek Links (Tomek Links) suppriment le chevauchement indésirable entre les classes où les liens de classe majoritaire sont supprimés jusqu’à ce que toutes les paires de voisins les plus proches, à distance minimale, soient de la même classe.

Les plus curieux pourront également s’intéresser au sous-échantillonnage par l’Edited Nearest-Neighbor et les NearMiss (1, 2 et 3) qui peuvent être paramétrés pour obtenir un sous-échantillonnage plus fort qu’avec les liens de tomek.

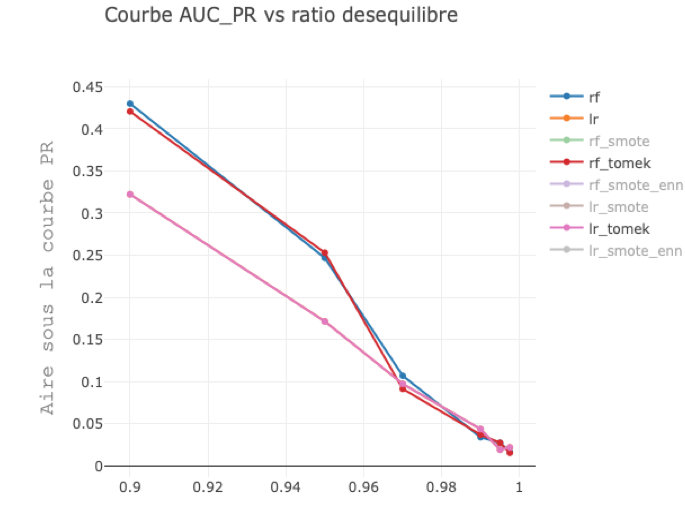
Performances obtenues avec et sans tomek links en utilisant une forêt aléatoire(rf) et une régression logistique(lr) pour un taux de déséquilibre variant.
Dataset généré avec make_classification de scikit-learn.

En ne considérant que l’obstacle que représente le déséquilibre de classes, sans considérer les autres caractéristiques du dataset, l’impact des tomek links est faible.

Oversampling

Le sur-échantillonnage (oversampling) consiste à rééquilibrer le jeu de données en augmentant artificiellement le nombre d’instances de la classe minoritaire.

Random Oversampling

Le sur-échantillonnage aléatoire (Random Oversampling) consiste à compléter les données de formation par des copies multiples de certaines d’instances de la classe minoritaire.

SMOTE — Synthetic Minority Over-sampling Technique

Plutôt que de reproduire les observations des minorités, le sur-échantillonnage des minorités synthétiques (SMOTE) crée un nombre (choisi par l’utilisateur) d’observations synthétiques sur les segments entre éléments proches de la classe minoritaire.

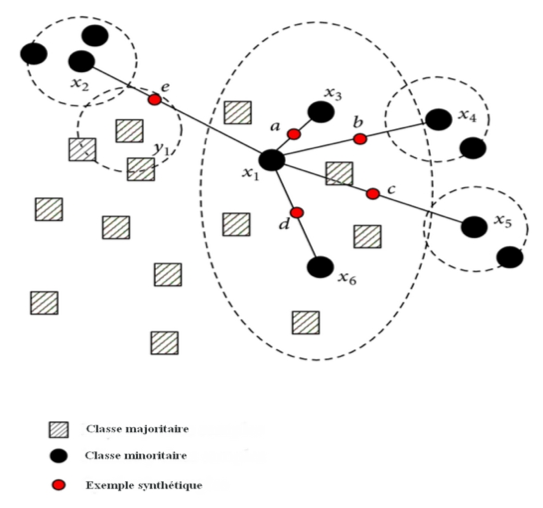
Les plus curieux pourront également s’intéresser aux variantes de smote disponible notamment dans le package python smote-variants.

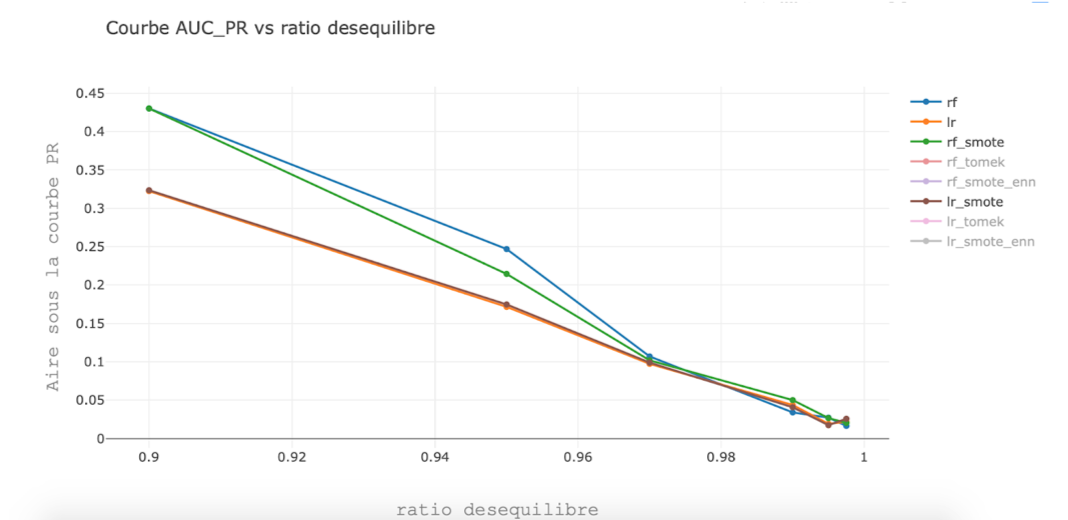
Performances obtenues avec et sans smote en utilisant une forêt aléatoire(rf) et une régression logistique(lr) pour un taux de déséquilibre variant.
Dataset généré avec make_classification de scikit-learn.

En ne considérant que l’obstacle que représente le déséquilibre de classes, sans considérer les autres caractéristiques du dataset, on remarque que smote a un impact positif, neutre, ou négatif sur la performance des deux algorithmes.

On comprend alors que le ré-échantillonnage n’est pas une solution miracle pour dans les situations de déséquilibre de classes. Il faudra aller plus loin dans l’analyse du jeu de données pour comprendre quand celui-ci est pertinent.

En dernier recours : le cost-sensitive learning

Avec le cost-sensitive learning, on montre un moyen possible de modifier l’étape d’apprentissage dans le cadre du déséquilibre de classes.

En théorie

Lorsqu’il est possible d’avoir une bonne estimation du coût de chaque type d’erreur ( faux positif et faux négatif), il peut être intéressant d’utiliser le cost-sensitive learning. Le cost-sensitive learning est le fait d’associer un coût différent à chaque type d’erreur. Il nécessite la définition d’une matrice de coût :

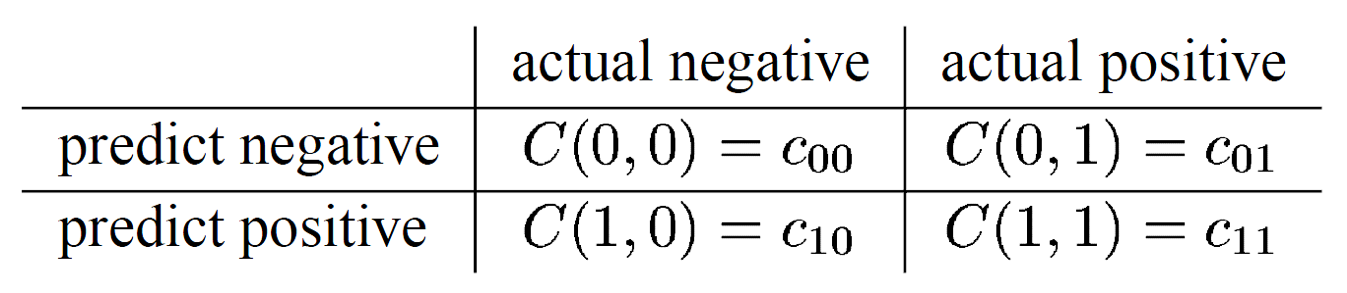
Dans ce cas, il sera judicieux d’utiliser une métrique directement liée à cette matrice de coût. Une fonction de coût comme celle ci-dessous pourrait être utilisée comme métrique :

Pour être encore plus fin, on peut définir une fonction de coût pour chaque type d’erreur et avoir un coût spécifique pour chaque exemple. Alejandro Correa Bahnsen a créé un package, CostCla, dans ce but et a appelé cette technique « Example-Dependent Cost-Sensitive Learning » : pour chaque exemple i, un coût calculé. Il nécessite une matrice de coût différente, appelée matrice de fonction de coût :

Le cost-sensitive learning permet de répondre directement à la problématique voulue. Par exemple dans le cas de la détection de fraude, le but étant de perdre le moins d’argent possible, d’une part en laissant passer trop de fraudes et d’autre part en étant trop stricte avec ses client, il sera possible de définir une fonction de coût pour chaque type d’erreur avec l’aide d’un expert. Ainsi en minimisant une fonction de perte incluant ces coût spécifiques, on minimise directement les pertes de la banque.

En pratique

En pratique, le cost-sensitive learning peut être appliqué très simplement sur la plupart des librairies machine learning (sklearn, lightgbm, xgboost…). Sur scikit-learn, la plupart des modèles de classification ont pour paramètre « class_weight ». Il sert à appliquer un coût inversement proportionnel au déséquilibre de classe. Visuellement, cela permet de débiaiser le modèle vers la classe minoritaire comme illustré ci-dessous où la frontière de décision d’un SVM à noyau linéaire est translatée vers la classe minoritaire.

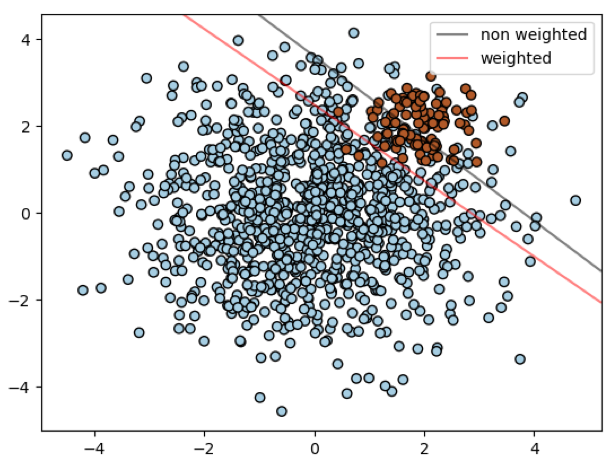
Vers la classification en général

Au delà du déséquilibre de classes

Le défi en classification est de parvenir à trouver une frontière de décision entre les classes. Cela peut passer par :

Le choix ou la conception puis optimisation d’un algorithme de classification
Un traitement de données approfondi.

En pratique c’est généralement la seconde méthode qui amène le plus de performance. Dans le cadre du déséquilibre de classes, on remarque que celui-ci ne fait qu’accroître la difficulté posée par d’autres caractéristiques propres au jeu de données. Un exemple, le coefficient de séparabilité (classe_sep) contrôlé dans la génération de jeu de données via make_classif de scikit-learn.

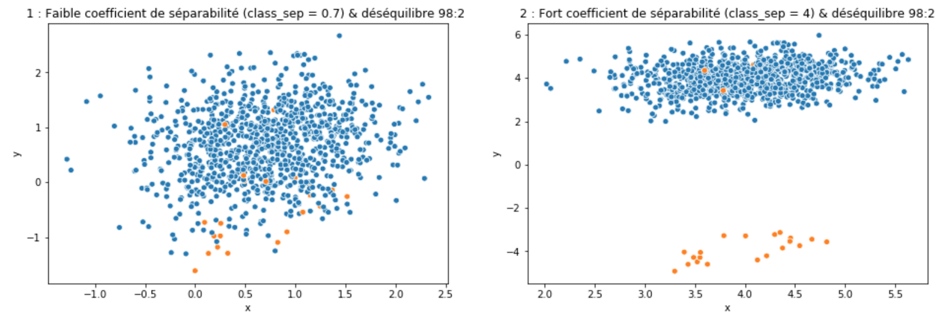
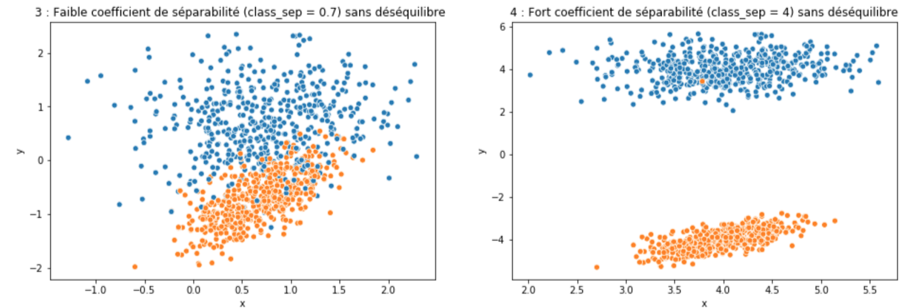
Les graphiques précédents montrent que :

Une classification présentant un déséquilibre de classe n’est pas nécessairement difficile (figure 2)
Que le déséquilibre de classe accroît la difficulté posée par les caractéristiques du jeu de données ( ici le coefficient de séparabilité de make_classif).

En effet le taux de déséquilibre présent sur le jeu de la figure 1 rend la classification plus difficile que celle présentée par la figure 3.

Pour aller plus loin sur la notion de séparabilité et de difficulté de classification, se référer aux articles [7], [8] et [9].

Que faire?

Finalement, il faut traiter un dataset présentant un déséquilibre de classes comme un autre. Il s’agira de passer plus de temps à modéliser le problème pour avoir, entre autres, une séparabilité de classe maximale. Cela passe notamment par :

Un feature engineering poussé pour générer des variables discriminantes (et augmenter la séparabilité)
Donc s’assurer d’avoir des données de bonne qualité pour éviter que le feature engineering ne soit que du bruit
Une réduction de la dimensionnalité
Une bonne définition de la cible avec pour s’assurer résout le bon problème (et donc qu’on a la bon nombre de positifs)
L’utilisation d’un ré-échantillonnage adapté
Puis le cost-sensitive learning avec une modélisation des coûts pertinente en dernier lieu.

La conclusion pour le data scientist : Un déséquilibre de classes demande de passer plus de temps à modéliser le problème et à comprendre le jeu de données. Donc il ne fera que rendre le challenge plus intéressant !

✍ Article écrit par Gaël Kengmegni

Merci à Benoît Lebreton et Michaël Sok pour leur relecture.

Références

[9] How complex is your classification problem ? : https://arxiv.org/abs/1808.03591