Comment apprend-on aux machines à tuer des aliens?

Le challenge ViZDoom

Enseigner à une machine à tuer, et à le faire bien : tel est le fruit issu du travail de chercheurs de Carnegie Mellon University. Derrière cette introduction volontairement provocatrice, les auteurs ont développé un algorithme de machine learning capable de prendre les commandes de Doom, le célèbre jeu vidéo sorti en 1993, dans le cadre du challenge ViZDoom. Ce dernier met à disposition une API permettant de simuler des parties, en fournissant à l’utilisateur des informations visuelles brutes, tout ceci à des fins de recherche sur l’intelligence artificielle et l’analyse d’image. Dans ce jeu de tir à la première personne, le joueur a pour but de se mouvoir dans un décor en 3D, et d’éliminer d’éventuels ennemis.

 Vidéo de l’IA aux commandes de Doom, en configuration deathmatch[1].

Alors que la plupart des études similaires ont lieu dans des jeux en 2D, ce travail se distingue notamment par le fait d’utiliser un algorithme d’apprentissage par renforcement dans des environnements en 3D, impliquant une vue partielle de l’état du jeu (limitée par la vision du joueur), et une vue à la première personne. De plus, jouer à Doom nécessite plusieurs compétences clés : naviguer dans un environnement en 3D, récupérer des objets, ainsi que reconnaître des ennemis. Même si la machine a encore besoin de 3 moteurs différents pour naviguer, détecter les ennemis, et tirer, elle peut néanmoins surpasser l’IA native, et mieux jouer que des humains dans des parties multijoueurs.

Apprentissage par renforcement

Mais comment cette Intelligence Artificielle (IA) a-t-elle appris à jouer seule dans cet univers complexe ? Elle s’inspire en grande partie des algorithmes d’apprentissage par renforcement (ci-après RL pour Reinforcement Learning) utilisés entre autres par l’équipe de Google DeepMind. On se rappelle notamment des travaux de cette même équipe de recherche dans l’apprentissage des jeux ATARI surpassant même dans certains cas un joueur humain expert (voir Figure ci-après). La propriété remarquable, commune à toutes ces IA, est de s’appuyer uniquement sur les données brutes du jeu : les pixels, les commandes disponibles, et le score ; tel un humain.

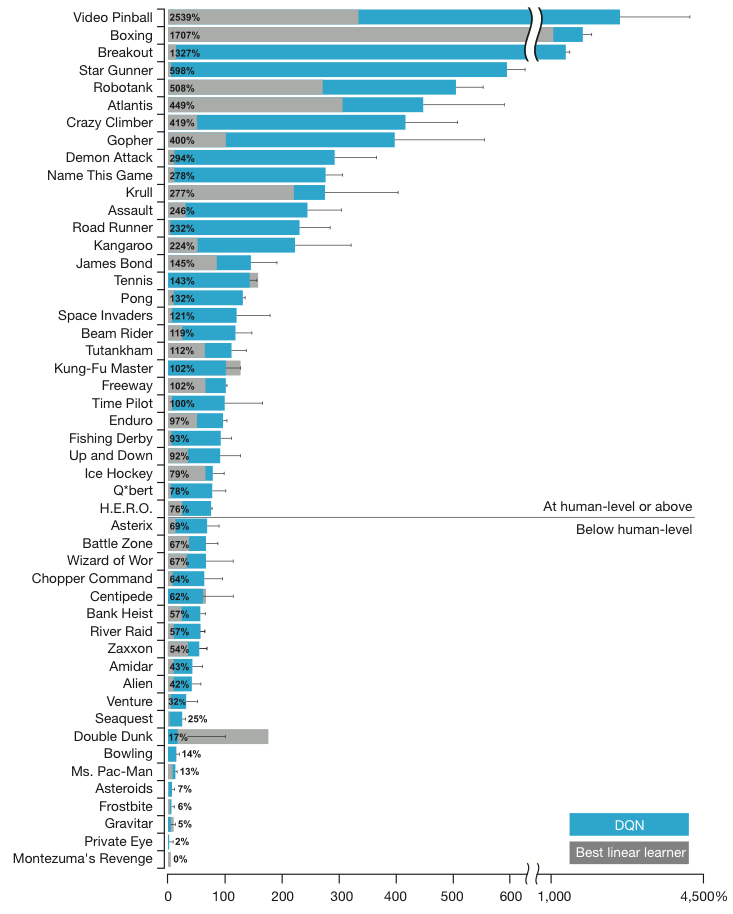
Comparaison entre l’agent développé par l’équipe de Google DeepMind (DQN pour Deep Q-learning Network) et les autres méthodes RL issues de la bibliographie. La performance est normalisé par rapport à un joueur humain professionnel (noté à 100%) et un joueur jouant aléatoirement (note à 0%). Crédit: Mhin et al, Nature (2013)

Cependant, enseigner à une machine à jouer, à partir directement des données visuelles, est un réel défi pour le RL. La plupart des applications de RL s’appuient en effet sur des représentations spécifiques des données du jeu grâce à l’intervention d’une entité humaine. Dans le cas présent, l’innovation réside dans cette capacité, sans aucune intervention humaine, à apprendre à partir d’un signal complexe, bruité, avec des enjeux de court et de long terme. En effet, le délai avant lequel une action peut conduire à une éventuelle récompense atteint parfois des milliers de pas de temps. Par ailleurs, les données reçues ont une corrélation temporelle très forte. Ces difficultés nous placent donc dans une situation aux antipodes des situations traditionnellement rencontrées en machine learning supervisé.

 Vidéo de l’IA jouant à l’un des plus célèbres jeux de ATARI des années 1970, casse-brique, dont le but est de détruire des briques à l’aide d’une balle, sans faire tomber cette dernière.

L’algorithme Q-learning

Cette section s’attardera sur la formalisation du RL, et plus particulièrement d’un de ses dérivés, le Q-learning, utilisé dans les travaux suscités. Le principe de cette technique est, pendant la phase d’apprentissage, de déterminer la meilleure action à effectuer, dans chaque situation ; puis, de rarement tenter une action alternative de façon à explorer des opportunités de meilleures récompenses (i.e. un meilleur score). Ainsi, l’algorithme trouve un compromis entre le risque de rater des opportunités de meilleure récompense, et le risque d’obtenir une récompense plus faible voire négative. Cette approche est d’une certaine manière similaire à l’algorithme du bandit manchot.

Pour cela, nous modélisons la situation par un Markov Decision Process (MDP). Dans ce contexte, le process (l’image envoyée par le jeu) peut se trouver dans un certain nombre n  d’états, chacun caractérisé par une récompense, c’est à dire le score. Le jeu peut passer d’un état à un autre avec une certaine probabilité, souvent représentée par une matrice de probabilité de transition (de taille n*n). Un agent (la machine simulant le joueur) peut influencer ce changement d’état au travers d’actions (les commandes du jeu).

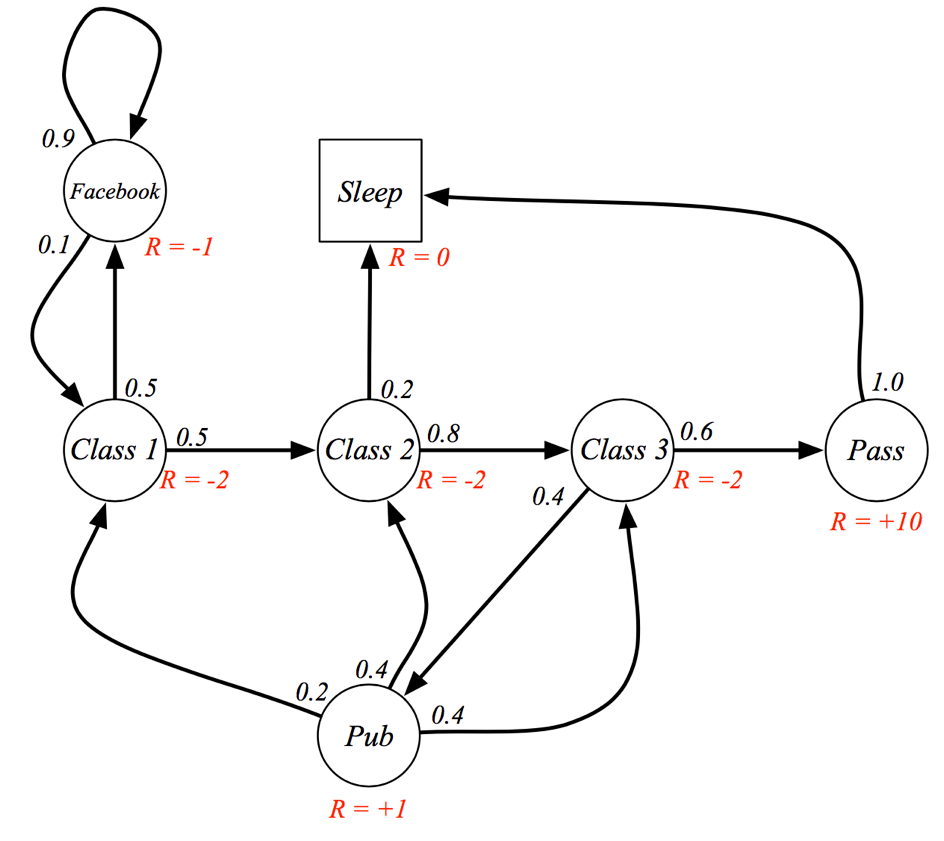
Le problème est donc de trouver pour chaque état, la meilleure action à entreprendre afin de maximiser son score. En d’autres termes, l’algorithme doit trouver la meilleure politique de jeu, un mapping entre une situation et une action, pour maximiser son score. Cependant, une action peut momentanément ne pas apporter une récompense immédiate, mais avoir une récompense ultérieure bien plus importante. Il peut donc exister un délai entre une action et la récompense. Pour prendre en compte cet aspect, il convient donc de sommer les récompenses dans le temps (jusqu’à un horizon temporel fini), suite à une action. L’importance d’une récompense immédiate par rapport à une récompense future est contrôlée par un paramètre d’affaiblissement compris entre 0 et 1. Lorsque ce paramètre vaut 0, alors l’algorithme va privilégier uniquement les récompenses immédiates (on parle de myopie temporelle). Au contraire, si ce paramètre vaut 1, alors il privilégiera les récompenses futures (on parle d’hypermétropie temporelle).

Connaissant la probabilité de transition d’un état à un autre (plus ou moins bien estimée par la taille du jeu d’entraînement), l’ensemble des états possibles, et l’ensemble des actions possibles, nous pouvons en principe calculer la politique optimale du jeu. Cependant, l’espace des états (et parfois des actions) étant astronomiquement large, il est numériquement impossible à ce jour de calculer directement cette solution[2]. Il est par conséquent nécessaire de se rabattre vers une solution numérique approchée, le Q-learning. Ce dernier est un algorithme cherchant à trouver itérativement, par essais et corrections successifs, la meilleure récompense possible, ajustant à la volée sa politique de jeu jusqu’à se stabiliser vers un score optimal. Rappelons qu’au cours de ces itérations, l’algorithme tente aléatoirement des actions alternatives (par rapport à celle jugée la meilleure) pour « explorer » de nouvelles possibilités (algorithme dit ε-greedy).

Enfin, afin de lever la corrélation temporelle entre des états successifs, plutôt qu’un apprentissage online plus traditionnel, il est courant d’utiliser la méthode experience replay (Lin 1993). Au lieu d’exposer l’agent à une image, on lui présente des séquences d’images nommées épisodes, que l’on range ensuite dans l’experience memory. Puis, on tire aléatoirement des séquences de cette dernière pour entraîner l’algorithme. Un second avantage de cette approche est d’éviter l’apprentissage de situation particulière de jeu. Par exemple, si pendant un certain temps l’action « tourner à gauche » est la meilleure action à prendre, alors les paramètres de l’algorithme peuvent rester bloquer dans ce minimum local. Tirer aléatoirement des épisodes permet ainsi de moyenner les expériences passées et éviter ces phénomènes d’oscillation d’action.

L’approche décrite ci-dessus suppose que l’agent a une vision complète de l’état du jeu. Nous n’aborderons pas dans cet article les subtilités apportées par la vision partielle du système. Cette dernière, ajoute certes une couche de complexité supplémentaire, mais ne change pas fondamentalement le principe de l’algorithme.

L’osmose entre machine learning et jeux vidéo

Les jeux vidéo offrent un terrain plus qu’idéal pour les recherches en machine learning. L’environnement est parfaitement contrôlé, et l’on peut à loisir varier chaque paramètre d’exécution, et enregistrer toute donnée nécessaire à l’étude. De nombreuses initiatives ont ainsi vu le jour, à l’image de ViZDoom. Par exemple, ce récent article applique un algorithme de RL au jeu de stratégie temps réel Starcraft dans lequel le joueur doit construire une armée et contrôler individuellement chaque unité dans le but de détruire l’armée adverse. La difficulté de ce jeu, d’un point de vue IA, réside dans la nécessité de prendre le contrôle d’un large nombre d’unité (typiquement quelques centaines) dans un environnement vaste mais seulement partiellement observable (dû au brouillard de guerre). De plus, le joueur doit à la fois gérer