Peut-on confier des calculs sur des données sensibles à un tiers sans lui faire totalement confiance ?

Peut-on confier des calculs sur des données sensibles à un tiers sans lui faire totalement confiance ?
Problématique :
La Data peut apporter énormément de valeur aux entreprises, mais elles doivent pour cela maîtriser l’énorme volume des données et parfois la vélocité avec laquelle les données sont acquises. Pour ne pas être débordées, il faut disposer de moyens de calculs importants, qui ne sont pas forcément accessibles à toutes les entreprises.
C’est pourquoi des acteurs ont émergé pour vendre de la puissance de calcul et de l’espace de stockage sur le Cloud. Ceci soulève une nouvelle problématique : si les données apportent de la valeur, elles sont stratégiques. Peut-on donc les confier à un tiers sans les crypter ? Mais si elles sont cryptées comment ce tiers pourra-t-il effectuer tous les calculs nécessaires pour en extraire la valeur ?
Au-delà des données stratégiques, ces questions s’appliquent à toutes les données sensibles, par exemple dans le domaine médicale. Avec ce type de données, même si les variables ne sont pas directement identifiantes, il reste facile d’identifier des dates, une taille, un poids ou un âge, afin de recouper les informations pour identifier les patients. L’anonymisation des données n’est donc pas suffisante. Un autre exemple est celui des données géolocalisées. Des données de latitude et de longitude sont facilement identifiantes et exploitables. En effet, même si le nom des variables n’est pas explicite, une fois leur nature identifiée, il n’y a que deux solutions à tester pour retrouver la localisation des observations. Cette faille peut être problématique les libertés individuelles mais également pour l’activité elle-même, par exemple si le lieu identifié est une base militaire ou un laboratoire d’expérimentation animale.
Cryptage classique et limites :
La solution pour empêcher toute exploitation des données est évidemment de les modifier pour les rendre méconnaissables. C’est ce que réalise le cryptage. Ainsi, dans une approche de cryptage classique, on considère deux interlocuteurs : l’émetteur et le récepteur. L’émetteur applique une transformation sur un message (qui peut être un texte comme un tableau de données). Cette transformation est réalisée par l’algorithme de cryptage et dépend en général d’une paire de clés : la clé publique qui permet le chiffrement des messages, et la clé privée qui permet le déchiffrement des messages.
Lors d’un échange de données cryptées classique, le récepteur a au préalable envoyé à l’émetteur une clé à partir de laquelle le message est chiffré (la clé publique). L’émetteur envoie donc un message crypté grâce à la clé publique fournie par le récepteur. Le récepteur décode le message grâce à un algorithme de décryptage et une clé qui n’est connue que de lui (la clé privée). Si un message doit être renvoyé en réponse à l’émetteur, alors il devient le récepteur, et le schéma s’inverse : le message est crypté grâce à sa clé publique, et il le décrypte avec sa clé privée.
Pour que ce système fonctionne, les deux clés doivent être distinctes, on parle de chiffrement asymétrique. Un exemple de chiffrement asymétrique est le protocole RSA (ici en version simplifiée) :
Le choix de la clé publique et le cryptage des messages suivent le protocole suivant :
- choisir 2 nombres premiers p et q
- calculer n, tel que n = pq
- choisir un entier e parmi de façon judicieuse (les concepts mathématiques qui permettent de choisir sont très avancés et dépassent le périmètre de cet article)
- le message m est crypté, donc transformé en message c : c = me mod(n)
La clé publique est donc le couple (e, n).
Pour décrypter le message, il faut trouver la racine eme modulo n de c. Ce calcul est facile si p et q sont connus. Mais, il est très difficile de trouver p et q à partir de n. En pratique la clé privée est l’inverse de e modulo n, noté d : m = cd mod(n). d conserve donc toute l’information concernant p et q ainsi que le choix de e. n est quant à elle obtenue à partir de la clé publique.
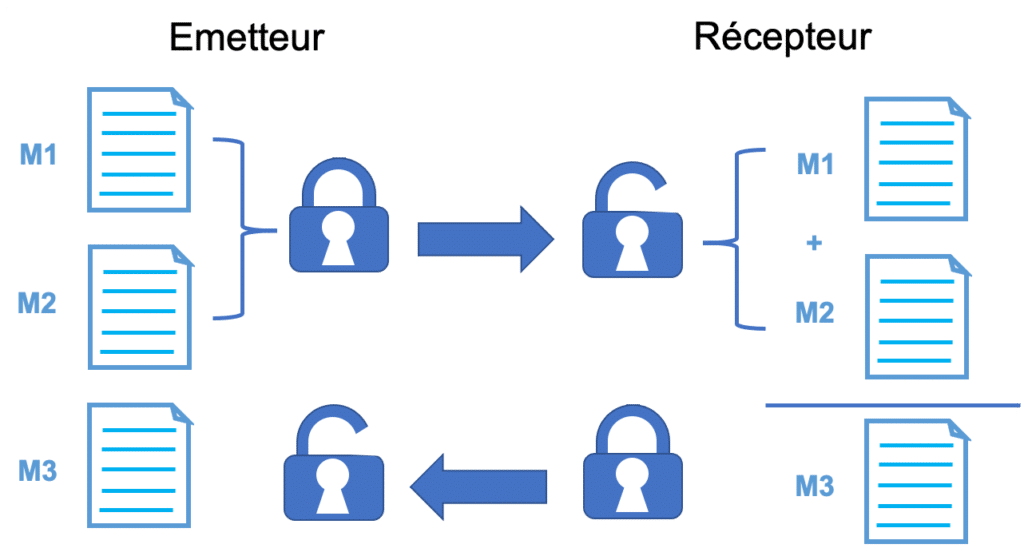 |
| Figure 1 : Echange de données avec un cryptage classique |
L’approche classique présente deux défauts : 1) elle implique un partage de clé entre les deux interlocuteurs, qui peut donc être interceptée par un tiers, et 2) le récepteur peut décoder les données qui deviennent donc accessibles par son biais. L’approche permet donc potentiellement d’accéder aux données via le cloud provider. En fait, elle ne sécurise que le transfert de données. En effet, les clés sont un moyen d’identification mutuelle des interlocuteurs, ce qui empêche un troisième acteur d’avoir accès à l’information qu’ils échangent. Mais elle ne résout pas le problème d’un récepteur auquel on ne ferait pas confiance.
Cryptage homomorphique :
Pour pallier les défauts mentionnés précédemment, il faut pouvoir utiliser les données cryptées pour les calculs et que l’émetteur n’ait plus qu’à appliquer l’algorithme de décryptage sur le résultat renvoyé. Il faut alors que le résultat décrypté soit équivalent à celui qu’on aurait obtenu sur les données avant cryptage. Cela implique que le cryptage doit conserver les caractéristiques mathématiques des données, une propriété appelée homomorphie. C’est pourquoi on parle de cryptage homomorphique.
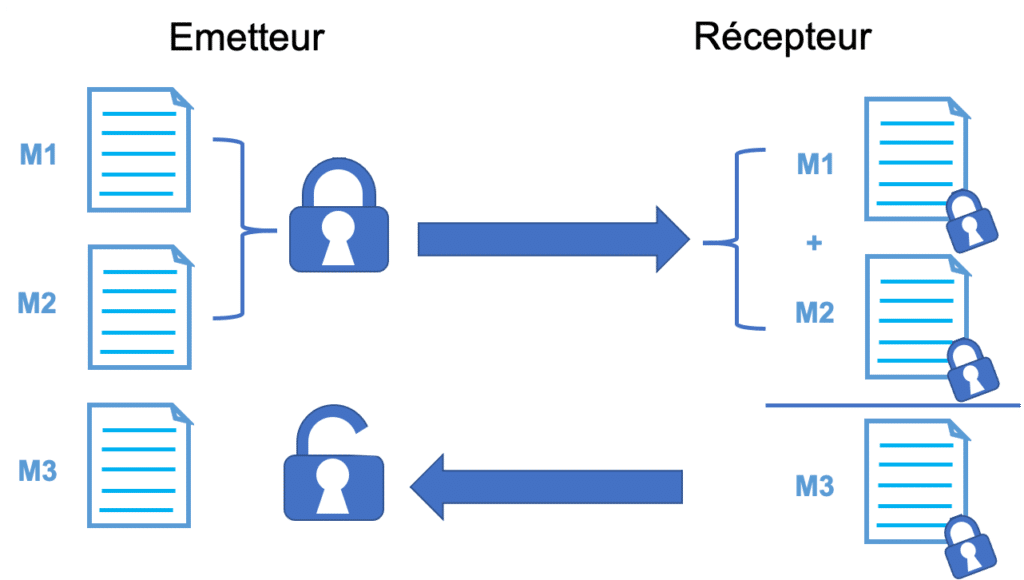 |
| Figure 2 : Echange de données avec un cryptage homomorphique |
Types de cryptages homomorphiques :
Le cryptage peut être caractérisé par les opérations pour lesquelles il est homomorphique. On distingue ainsi du moins complet au plus complet :
- le cryptage homomorphique partiel (PHE, Partial Homomorphic Encryption) qui ne permet qu’un type d’opération : addition ou multiplication
- le cryptage un peu homomorphique (SHE, Somewhat Homomorphic Encryption) qui permet les deux types d’opérations, mais seulement dans des séquences bien définies
- le cryptage complètement homomorphique nivelé (LFHE, Leveled Fully Homomorphic Encryption) : qui permet tout type d’opération mais seulement pour des séquences de longueur définie
- le cryptage complètement homomorphique (FHE, Fully Homomorphic Encryption) : qui permet tout type d’opération quelque soit la longueur de la séquence.
Un exemple de cryptage homomorphique partiel multiplicatif est le protocole RSA, dont le cryptage prend la forme : ε(m) = me mod(n). Considérant le produit de deux messages m1 et m2 :
ε(m1)ε(m2) = m1em2e mod(n)
ε(m1)ε(m2) = ε(m1m2)e mod(n)
ε(m1)ε(m2) = ε(m1m2)
Le cryptage RSA permet donc facilement le calcul des produits à partir des données cryptées.
Avantages :
L’avantage principal de ce type de cryptage, est évidemment de pouvoir réaliser les calculs directement sur les données cryptées. De plus, les solutions développées reposent généralement sur le principe de l’apprentissage avec erreur sur des anneaux (Ring learning with errors, RLWE). Brièvement, l’objectif de l’algorithme RLWE est de produire 3 ensembles de polynômes ai(x), ei(x), et s(x), à partir desquels on construit l’ensemble bi(x)= (ai(x) . s(x)) + ei(x). L’algorithme de génération employé garantit qu’il est extrêmement difficile, même avec un ordinateur quantique, de retrouver s(x) à partir de bi(x) et ai(x). Ces éléments servent donc de base pour un chiffrement robuste aux attaques.
Inconvénients :
Le RLWE est en fait utilisé pour générer des cryptages SHE. En effet, ei(x), et s(x) agissent comme des perturbateurs du message qui y ajoutent du bruit. Plus on effectue un grand nombre d’opérations sur les messages cryptés, plus le bruit s’accumule jusqu’à rendre le message indéchiffrable. Pour obtenir un cryptage FHE deux approches ont principalement été employées : l’optimisation du niveau de bruit et le “bootstrapping”. Ce dernier consiste à évaluer homomorphiquement (c’est à dire sans revenir à un état décrypté) la procédure de décryptage au cours des calculs afin de réduire le bruit. Quelque soit la solution employée, le passage d’un cryptage SHE à un cryptage FHE augmente le temps de calcul. C’est pourquoi différentes optimisations ont été développées, chacune aboutissant à un algorithme de FHE différent. D’autres implémentations imposent des contraintes sur l’homomorphisme (le cryptage n’est donc pas FHE), ce qui facilite les calculs.
Un autre inconvénient est une conséquence de la transformation des données. En effet, dans l’exemple du protocole RSA, la multiplication des messages chiffrés peut être directement déchiffrée. Mais selon la transformation appliquée aux données, les opérations peuvent demander des adaptations supplémentaires. Par exemple, dans le cas de chiffrements reposant sur le RLWE, l’addition de deux messages cryptés peut être effectuée directement, mais leur multiplication demande des adaptations. En effet, si on considère le produit de deux messages chiffrés, (en omettant le message initial pour simplifier l’expression), on obtient l’expression suivante : bb’ = (as + e) (a’s + e’) = aa’s2+ase’ + a’se + ee’. Le bruit s est donc passé au carré ce qui rend le message indéchiffrable. Pour éviter cela, on calcule plutôt le produit d’une transformation (cette fois le message initial est conservé) : b -as = 2e + m, d’où (b – as) (b’ – a’s) = (2e +m) (2e’ +m’) = 4ee’ + 2em’ +2 e’m +mm’. Ce produit est alors déchiffrable, tout en dépendant toujours du produit des messages en clair mm’.
Exemple d’application : le e-voting
Disons que nous avons trois candidats pour une élection : Alex, Bob et Charline. Chacun peut être représenté par un code binaire : respectivement 01 00 00, 00 01 00, 00 00 01. Le tableau suivant donne les résultats de l’élection.
| Alex | Bob | Charline | Bit Score |
| x | 00 00 01 = 1 | ||
| x | 00 01 00 = 4 | ||
| x | 00 01 00 = 4 | ||
| x | 00 00 01 = 1 | ||
| x | 01 00 00 = 16 | ||
| x | 00 00 01 = 1 |
Pour calculer le résultat de l’élection sur des données cryptées, nous avons besoin d’un homomorphisme additif. L’algorithme de chiffrement utilisé sera celui de Paillier. En bref :
- l’algorithme commence par choisir deux nombres premiers p et q, et définit n = pq
- il définit λ(n) = lcm(p -1, q-1), le plus petit multiple commun à p-1 et q-1
- il choisit gtel que L(gλ mod(n2)) est inversible modulo n, avec L(u) = (u -1) / n ; L, n et g sont la clé publique, p et q sont la clé privée
- il choisit r aléatoirement
- il chiffre un message m : c = gx rn mod(n2)
- pour le déchiffrer : m=L( cλmod(n2)) / L(gλ mod(n2)) mod(n)
Soient p = 5, q = 7, donc n = 35. Alors λ =12, et g= 121 (aléatoire). Le tableau suivant montre le chiffrement obtenu, en fonction de r :
| m | r | enc(m, r) |
| 1 | 4 | 359 |
| 4 | 17 | 173 |
| 4 | 26 | 486 |
| 1 | 12 | 1088 |
| 16 | 11 | 541 |
| 1 | 32 | 163 |
Pour effectuer la somme de nos votes après la transformation de Paillier, il faut calculer le produit de nos données chiffrées modulo n2:
359⋅173⋅486⋅1088⋅541⋅163=983 mod 1225
Il suffit ensuite d’appliquer la procédure de décodage :
- L(cλmod(n2)) = L(98313 mod(1225)) = (36 -1) / 35 = 1
- L(gλmod(n2)) = L(14112 mod(1225)) = (456 -1) / 35 = 13
- m = 1/13 mod(35) = 27
Une fois décodé, on obtient 27, qui en binaire donne 01 10 11. Comme les deux premiers bits correspondent à Alex, le total de votes le concernant est 1 (01). Les deux suivants correspondent à Bob, qui a donc obtenu 2 voies (10). Enfin, les derniers correspondent à Charline qui a donc obtenu 3 voies (11).
Implémentations disponibles :
Plusieurs librairies open source sont actuellement disponibles pour faire du cryptage FHE, en particulier :
- SEAL : développée par Microsoft en 2019, et utilisable dans des programmes maison et sur Azure
- HElib : développée par IBM en 2014
- PALISADE : développée par un consortium d’entreprises de défense financées par la DARPA et d’universitaires en 2019
De plus, les Confidential VMs disponibles sur GCP utilisent ce type de cryptage.
Conclusion :
En résumé, le cryptage homomorphique permet d’effectuer des calculs sur des données cryptées sans avoir à les décrypter. Le chiffrement étant assuré par un algorithme robuste aux attaques, il est parfaitement adapté pour les données suffisamment sensibles pour ne pas pouvoir être confiées à un tiers.
Toutefois, les techniques de chiffrement actuelles peuvent nécessiter d’adapter les calculs selon la transformation utilisée. De plus, l’utilisation d’un chiffrement totalement homomorphique augmente fortement le temps de calcul des applications. Pour cette raison, les développements actuels visent à optimiser les calculs sur les données chiffrées, ou à garantir un homomorphisme plus restreint, adapté à des situations fréquentes.
Le chiffrement homomorphique est actuellement peu utilisé, ce qui est probablement lié à son haut niveau de technicité et à la jeunesse des implémentations disponibles. Toutefois, avec le développement du calcul sur le cloud, il est très probable que ce type chiffrement se généralise très rapidement. En effet, en permettant de faire des calculs sur une infrastructure tiers sans avoir à lui accorder une totale confiance sur la confidentialité des données, le cryptage homomorphique est une excellente solution de protection des données personnelles et sensibles.
Références :
Homomorphic encryption – Wikipedia
Chiffrement homomorphe — Wikipédia
Ring learning with errors – Wikipedia
https://brilliant.org/wiki/homomorphic-encryption/

