Intelligence Artificielle et Data Quality : comment corriger des données historiques impactées par la Covid 19 pour améliorer la qualité des prévisions ?
Des prévisions enrayées par la crise
La crise sanitaire de la COVID19 a fortement perturbé le fonctionnement de la plupart des secteurs de l’économie. Le ralentissement globalisé de l’activité pendant les différents confinements a causé l’apparition de périodes temporelles atypiques sur les observations effectuées a posteriori.
Ces perturbations ont engendré l’émergence d’un nouveau défi pour les projets d’analyse prévisionnelle : la capacité de gestion et de traitement d’un historique affecté par un événement perturbateur ponctuel.
Nous avons exploré cette problématique au travers d’un cas d’usage dans lequel nous cherchons à estimer les appels passés dans un call center. L’objectif est de prévoir les appels quotidiens entrants afin d’optimiser le dimensionnement du nombre de téléconseillers. L’impact significatif des différentes périodes de confinement est facilement visible sur le jeu de données brut :
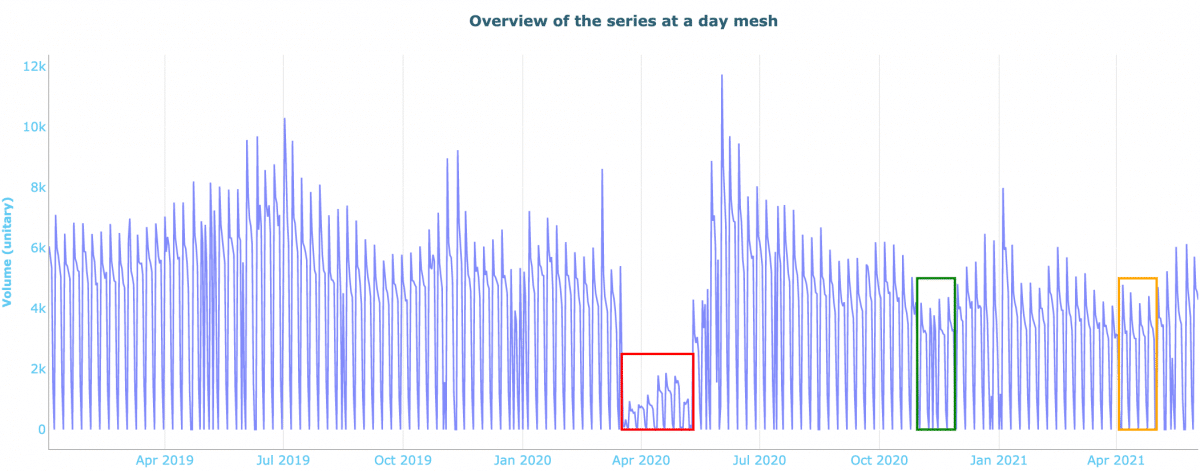
Impact significatif des différentes périodes de confinement
Nous avons commencé par effectuer une prévision classique en nous appuyant sur un modèle statistique dont le principe est de calculer les composants principaux d’une série temporelle (tendance et saisonnalités) en se basant sur son historique et afin de les extrapoler pour prédire l’avenir. Le modèle sélectionné est un modèle Prophet, qui a été choisi pour sa nature simple et facilement explicable, ainsi que pour la possibilité de choisir ses propres cycles saisonniers.
Les résultats obtenus sont directement influencés par les périodes de fluctuations, avec un effet particulièrement notable au niveau de la saisonnalité annuelle. Cet impact est amplifié par le manque de profondeur d’historique des données, impliquant que les saisonnalités (notamment annuelle) sont mesurées sur un faible nombre de motifs.
Le graphe ci-dessous présente l’explicabilité fournie par le modèle. On note la pénalisation sur le mois de mai, suivie d’un effet de rattrapage au mois de juillet (cercle rouge) :
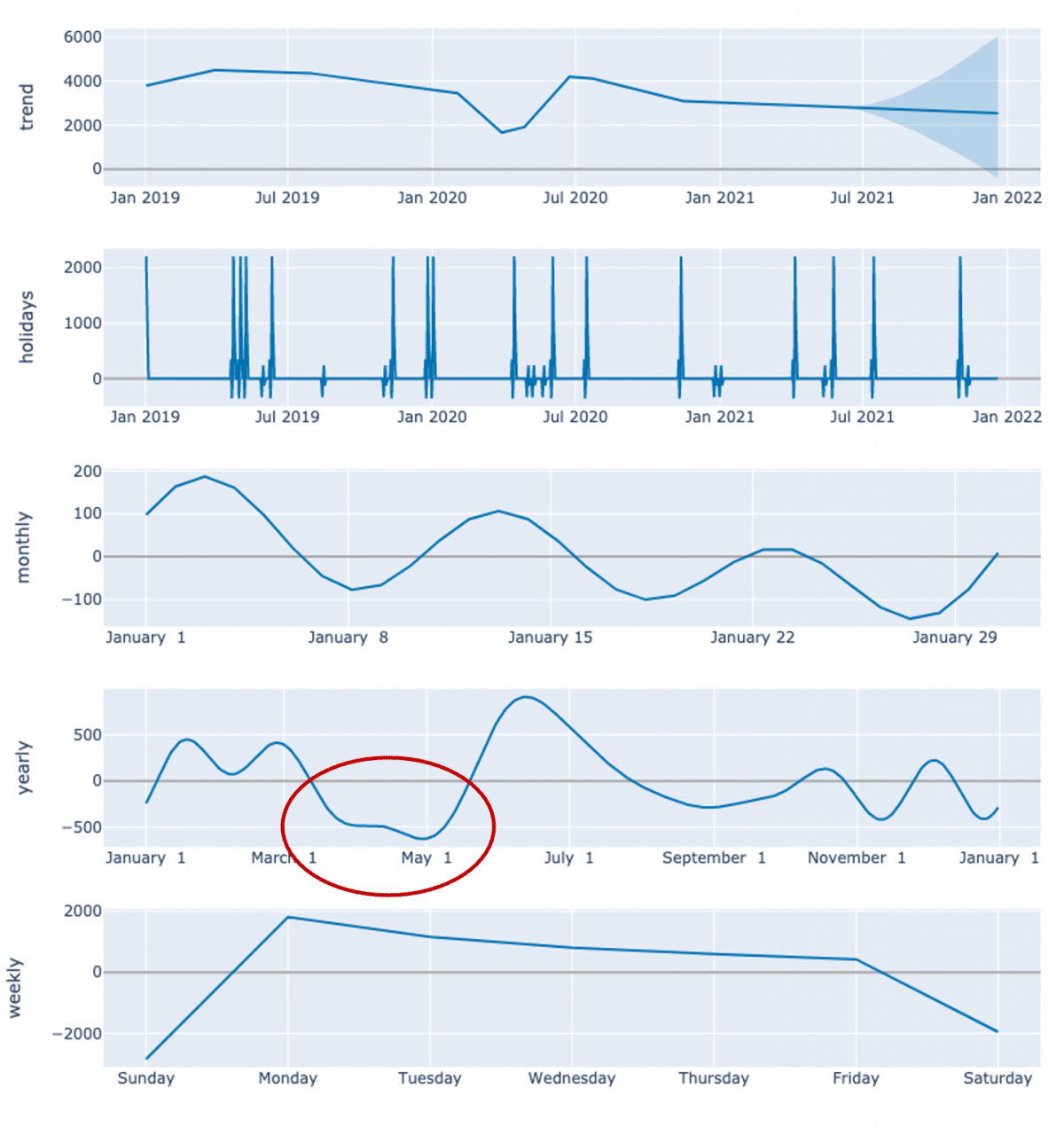
Explicabilité du modèle sans correction d’historique avec un biais sur les mois de mai à juillet.
Désireux de conserver cette saisonnalité annuelle car significative d’un point de vue métier, nous avons décidé de comparer différentes méthodes de correction d’historique dans le but de gommer les effets des différents confinements.
Nous avons pour cela mis en place plusieurs méthodes et comparé les résultats obtenus dans chaque situation. Dans la section suivante, nous présenterons les approches et leur principe, à savoir :
- L’imputation
- L’ajout de variable catégorielle
- Le transport optimal
- L’adaptation de domaine temporelle
Utilisation de méthodes de correction d’historique
1/ Imputation
Cette première approche est la plus naïve, mais aussi la plus simple à mettre en place. Elle consiste à effacer l’historique des plages de confinement pour reconstruire un historique sur la base du reste des données disponibles. Dans l’exemple ci-dessous, la reconstruction est faite en utilisant pour chaque valeur manquante celle de l’année précédente :
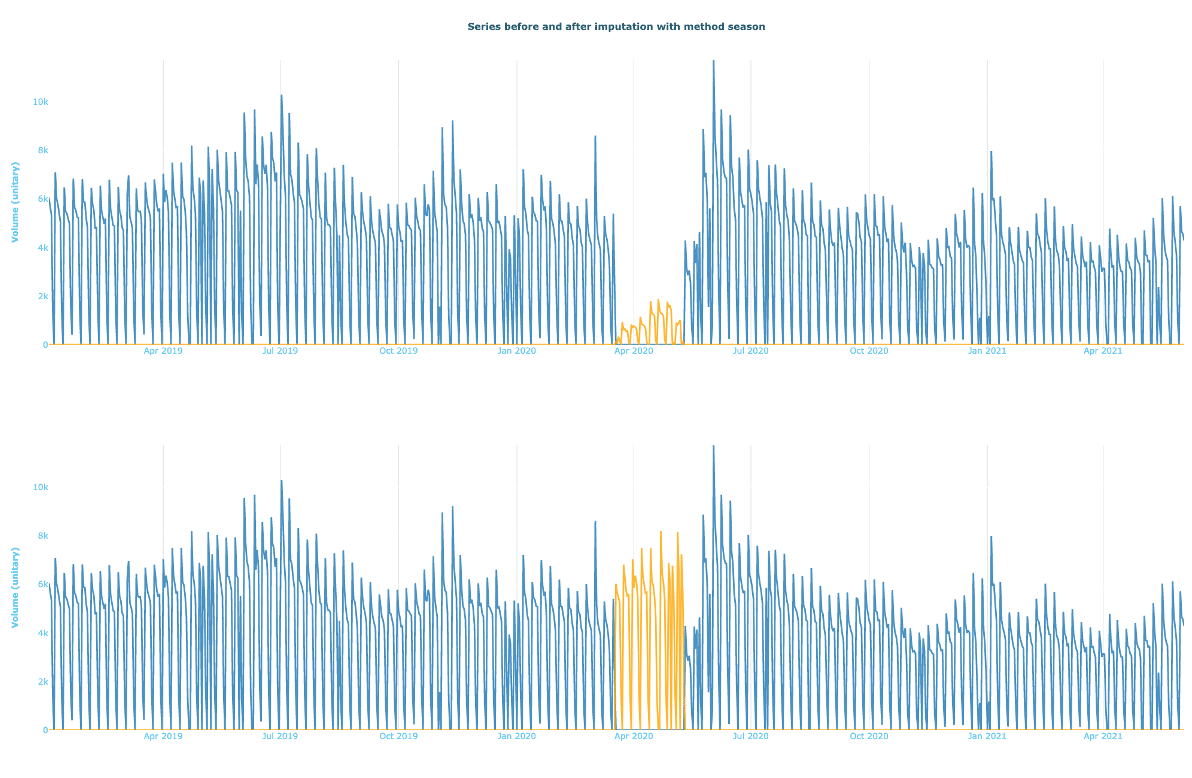
Jeu de données avant et après imputation par la valeur de l’année passée.
Bien que pratique, cette méthode possède le désavantage de ne pas tirer parti des mesures effectuées pendant les contextes « anormaux » (confinements). Elle possède aussi l’inconvénient de ne pouvoir fonctionner que dans un sens. Il est en effet nécessaire de se baser sur le contexte prédominant afin de reconstruire le ou les contexte(s) minoritaire (soit ici de passer d’une période COVID à une période hors COVID).
Les résultats obtenus grâce à cette approche sont meilleurs qu’avec notre première approche sans modification sur l’historique. La correction est en revanche trop forte et une partie de l’information est perdue. Cette méthode fait office d’une bonne première approche, notamment si la mise en place de la correction doit être rapide.
2/ Ajout de variables catégorielles
La seconde approche n’est pas réellement une approche de correction d’historique mais plutôt une approche de prise en compte des différents contextes existants dans l’historique. Elle consiste à marquer les périodes touchées par la crise en utilisant des variables booléennes, puis à intégrer ces variables synthétiques dans le modèle en tant que variables exogènes. Cette approche permet une considération des perturbations sans pour autant en modifier les valeurs. Très simple à mettre en place sur un modèle de prévision comme Prophet qui permet l’ajout de ce type de saisonnalité, elle se révèle également efficace dans notre cas d’usage.
L’effet résultant de cet ajout de variable est directement représenté dans la décomposition des saisonnalités faite par le modèle :
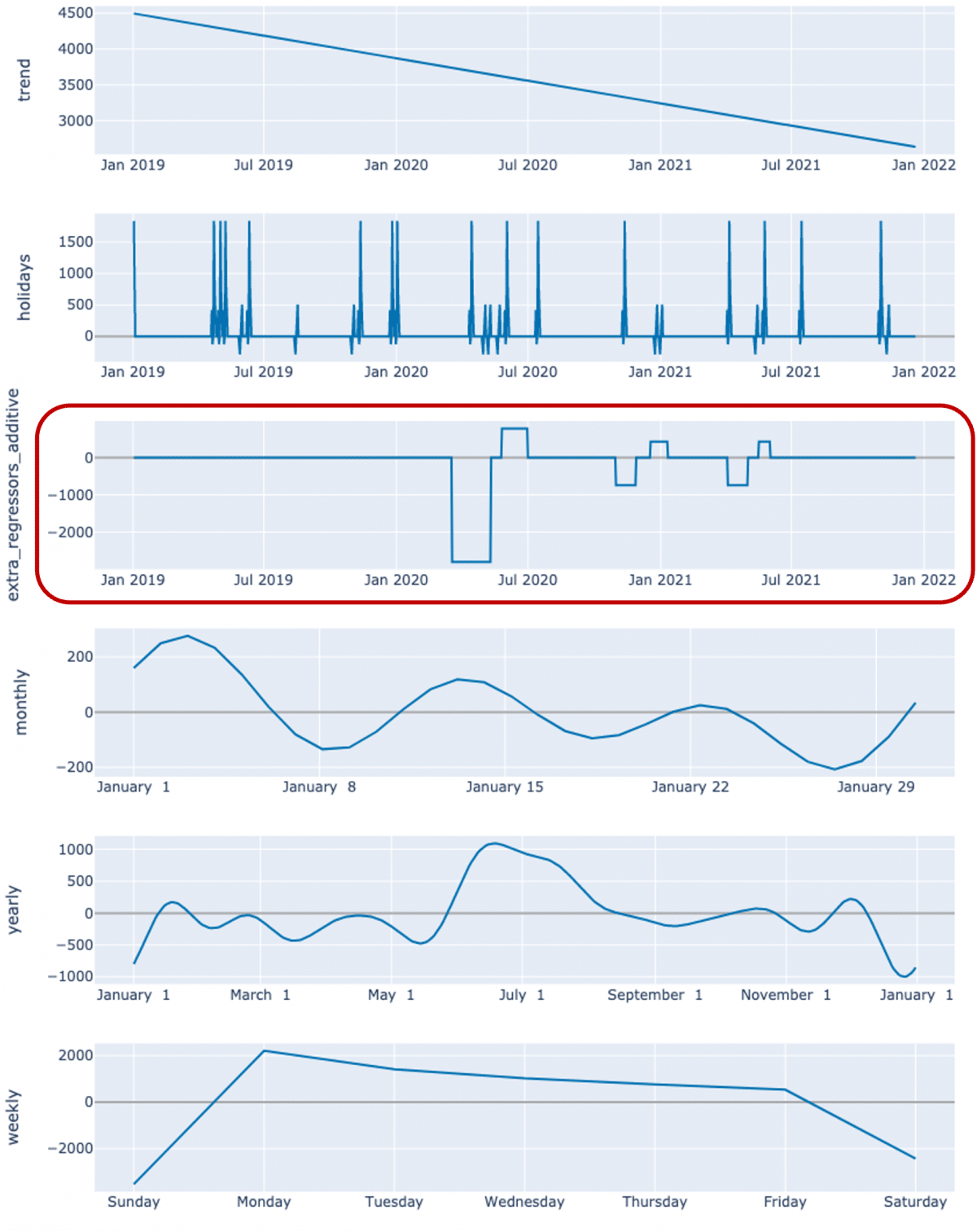
Explicabilité du modèle une fois les variables ajoutées (une variable pour le premier confinement, une pour les deux suivants, et de la même façon des variables pour les périodes de reprise post-confinement)
Le principal défaut de cette méthode vient de sa simplicité. En considérant l’ensemble des observations de chaque contexte de la même façon (c’est le principe des variables booléennes), la modélisation ne fait qu’ajouter une constante sur chaque période (ou contexte) considérée, ce qui est évidemment simplificateur par rapport à la réalité.
Elle permet en revanche de facilement passer d’un contexte à un autre lors de la modélisation, chose qui n’était pas permise par l’imputation.
Cette méthode pourrait être optimisée en remplaçant les variables booléennes par des variables continues mais cela nécessite leur bonne définition.
3/ Transport Optimal
Le transport optimal consiste à modifier la partie de l’historique correspondant à un contexte « anormal » et appelée contexte source (ici un confinement par exemple) pour la transporter dans un contexte dit cible (période hors confinement).
La transformation se base sur un principe d’optimisation sous contrainte, permettant le passage d’une distribution à une autre par le plus court chemin.
La distribution du nombre d’appels quotidien sur l’ensemble de l’historique représentée ci-dessous montre la transformation des données du premier confinement (contexte source) en bleu vers les données hors confinement (contexte cible) en vert. La distribution transformée est la courbe orange :
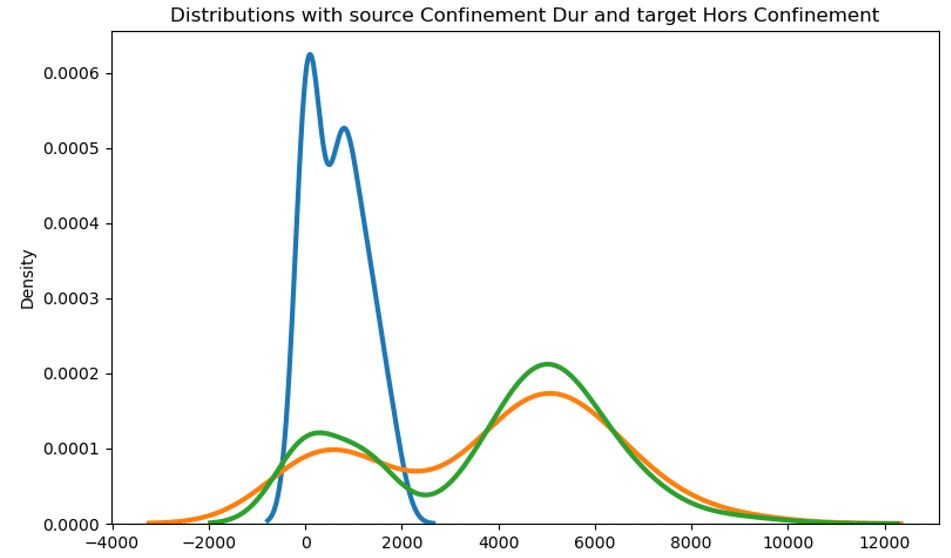
Illustration du principe de transport depuis la distribution source (bleu) vers la distribution cible (vert).
La distribution résultante est donnée en orange.
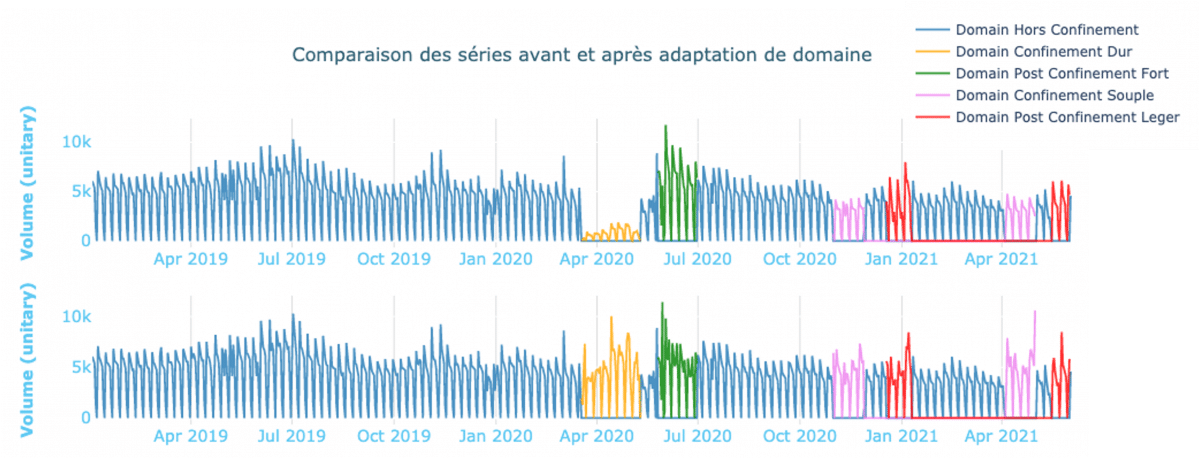
Cette opération de transport est appliquée depuis chaque domaine source vers le domaine cible désiré afin de progressivement modifier l’historique et de gommer la disparité entre les contextes, comme l’illustre le graphe ci-dessous.
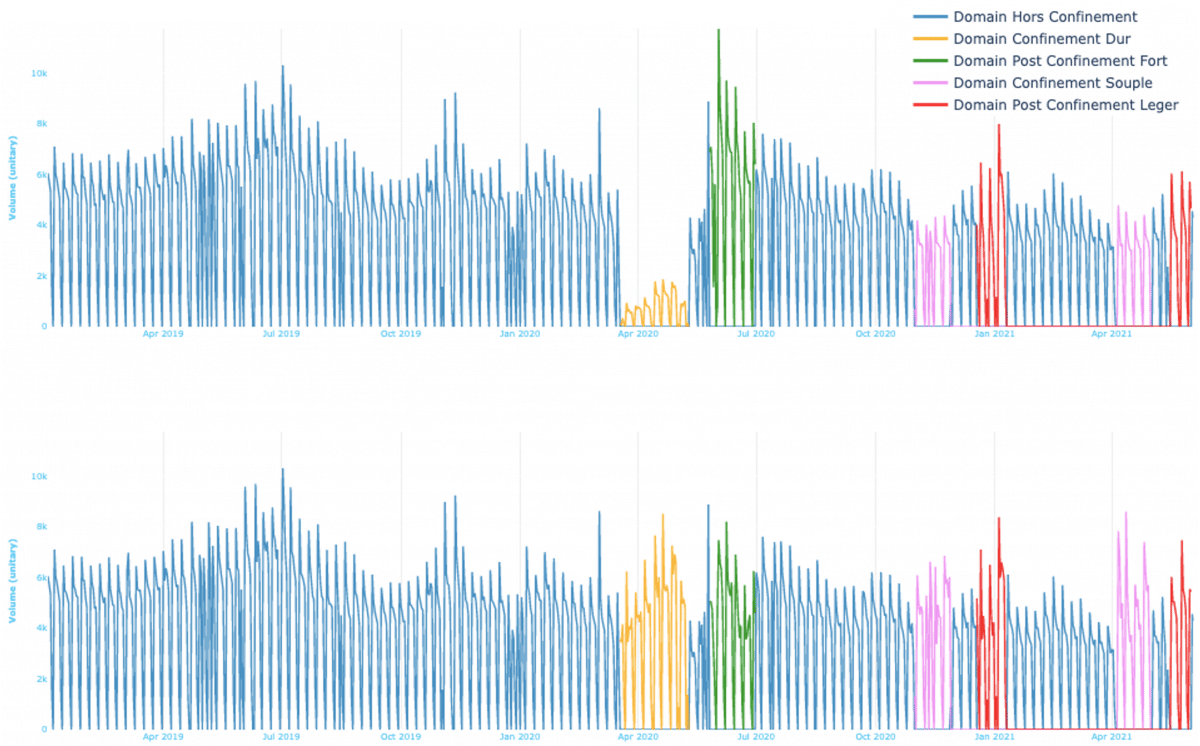
Jeu de données avant (haut) et après (bas) transport optimal vers le contexte hors covid (bleu).
Contrairement à l’imputation, cette approche s’appuie sur les données enregistrées pendant la période à modifier. Il n’y a donc pas de perte d’information : un pic dans le domaine à transformer sera retranscrit une fois le transport effectué.
Nous avons également intégré la notion de saisonnalité au sein de la transformation en séparant le transport par jour de la semaine. Cela permet de conserver la saisonnalité du domaine cible et de prendre chaque donnée de façon plus contextualisée.
Les performances obtenues sont satisfaisantes. Elles permettent par ailleurs de facilement jongler entre les contextes.
4/ Adaptation de domaine temporelle
La dernière approche que nous avons essayée est une méthode d’adaptation de domaine purement basée sur les caractéristiques temporelles des données.
Une série temporelle peut être décrite par trois composants : une saisonnalité, une tendance, ainsi que des résidus, qui forment la partie restante du signal (majoritairement des composants ponctuels et du bruit).
Il est possible de décomposer une série en s’appuyant sur chacun de ces termes soit en en faisant la somme (décomposition additive), soit en les multipliant (décomposition multiplicative).
Le principe de l’approche est d’agir séparément sur chaque composant de la série fragmentée au préalable en ses différents contextes. Les opérations réalisées sont les suivantes :
- Le motif saisonnier du contexte cible est conservé et appliqué à chaque contexte source.
- La tendance est extrapolée du contexte cible soit par régression linéaire, soit en appliquant une méthode de transport optimal.
- Enfin, les résidus sont normalisés par contexte, puis dé-normalisés via l’opération de normalisation inverse effectuée sur le contexte cible. Cette approche permet de « mettre à niveau » les résidus tout en en conservant la nature et le comportement.
Nous avons représenté à titre d’exemple l’évolution de la saisonnalité hebdomadaire entre le contexte « hors COVID » et la période de premier confinement. Une adaptation de domaine permettrait alors d’insérer le motif hebdomadaire « hors COVID » à la place du motif initial lors du transport d’un contexte vers le contexte « hors COVID ».
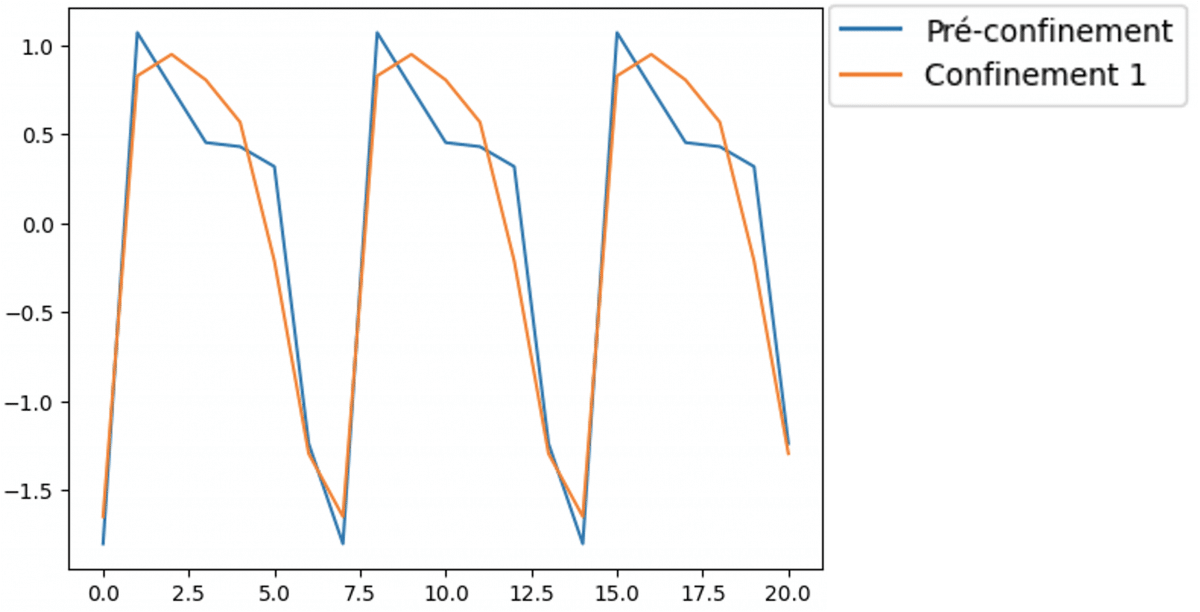
Exemple du changement de saisonnalité entre le contexte confinement et le contexte hors confinement.
Une fois chaque élément transformé individuellement, nous pouvons les combiner à nouveau pour reconstruire la série uniformisée.
Les résultats obtenus avec cette approche sont assez peu satisfaisants après modélisation, notamment parce que la série possède un motif saisonnier et une tendance qui sont assez variables au sein même du contexte hors covid. La période entre les confinements est en effet très volatile et il est difficile de bien définir chaque contexte.
Pour que cette approche soit réellement satisfaisante, il est nécessaire d’avoir des contextes bien définis et suffisamment stables.
Résultats obtenus
Nous avons réuni dans un tableau les résultats obtenus lors de la modélisation, qui intervient donc une fois l’historique corrigé.
Notons que la mesure de référence choisie est la RMSE, qui fait intervenir le carré de l’erreur sur la prévision et qui pénalise donc particulièrement les écarts élevés entre la prévision et la réalité.
Nous calculons aussi la MAPE, qui est l’erreur relative en pourcentage.
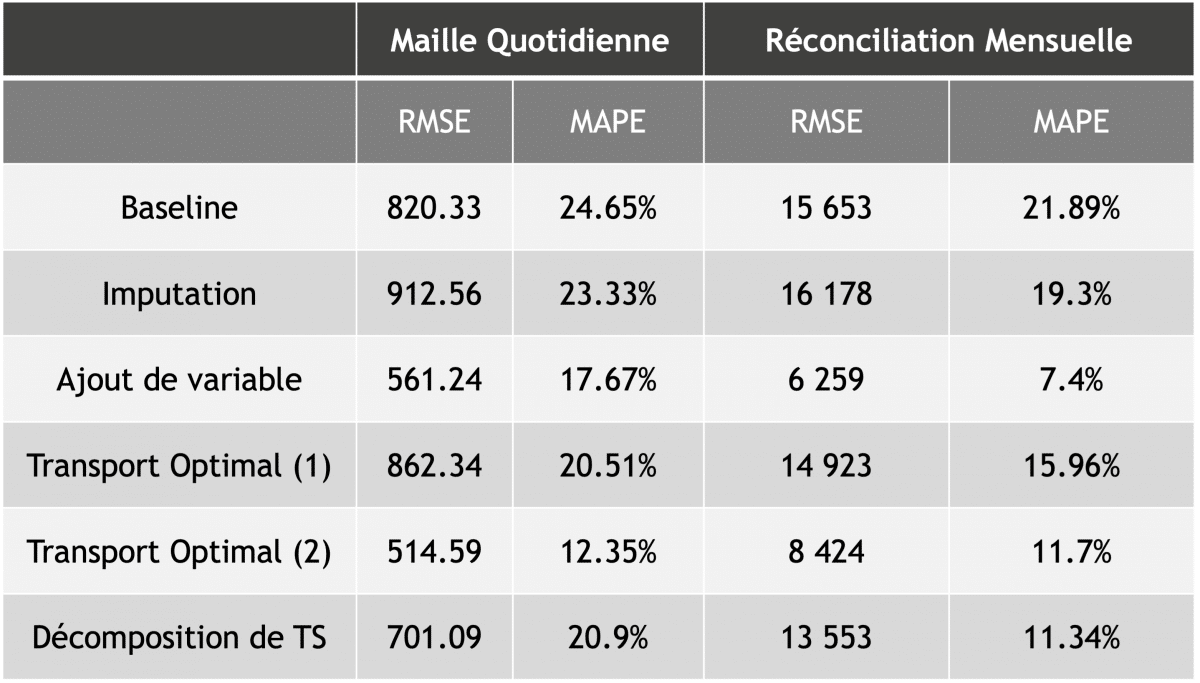
Les prévisions sont effectuées à une maille quotidienne, puis agrégées à la maille mensuelle, nous permettant ainsi d’identifier les biais dans les prévisions au travers des sur ou sous-estimations trop fortes.
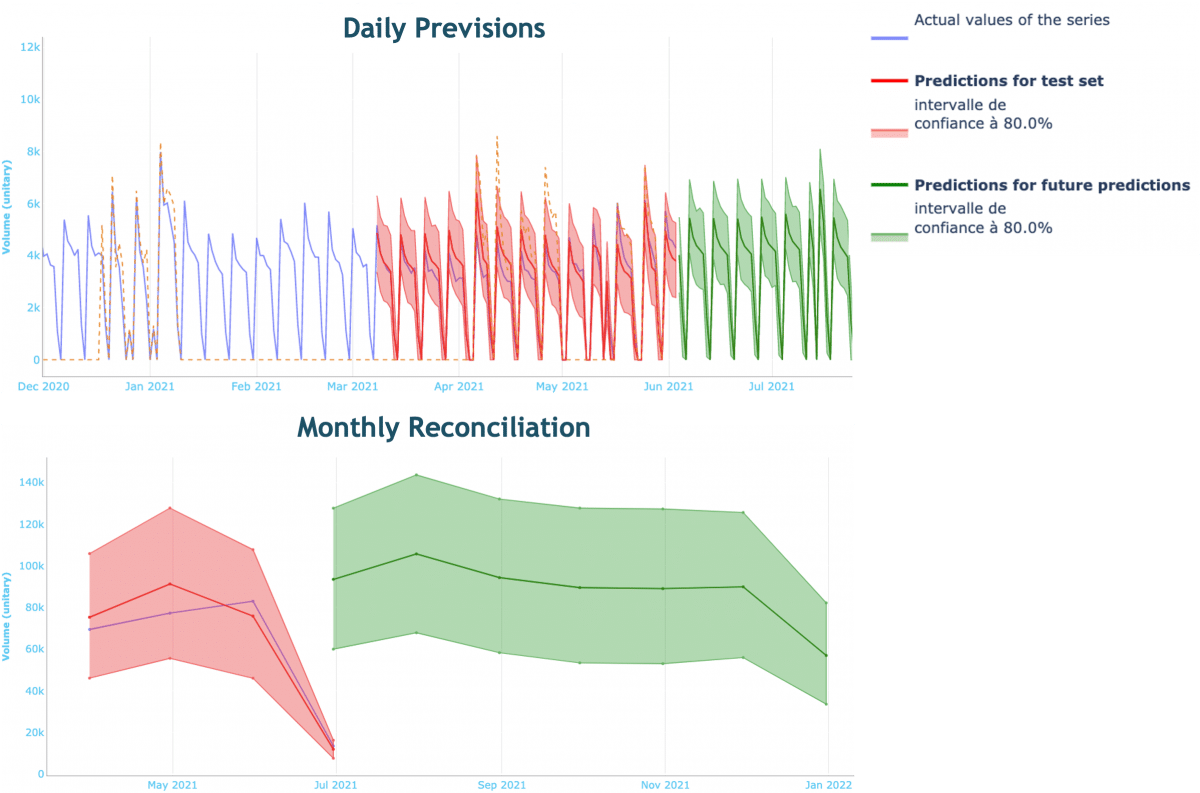
Aperçu des prévisions quotidiennes et de leur réconciliation.
Les résultats obtenus sont très satisfaisants : ils nous ont permis de baisser notre RMSE de 37% grâce à l’approche de Transport Optimal, soit une erreur améliorée d’environ 300 appels par jour en moyenne.
Conclusion sur les approches de correction d’historique
L’approche de transport optimal est celle obtenant les meilleures performances dans notre cas d’usage. Il est cependant important de garder en mémoire que chaque cas d’usage est unique et nécessitera de comparer plusieurs approches (visuellement ou par quantification) pour sélectionner celle correspondant le plus aux données.
La méthode adoptée dépend aussi du modèle de prévision choisi par la suite. Par exemple, un modèle ensembliste type Gradient Boosting sera bien adapté à la méthode de l’ajout de variable, à l’inverse des approches statistiques en général.
La correction d’historique est un sujet particulièrement applicable à la période de la COVID19. Son utilisation peut cependant être étendue à d’autres sujets mettant en œuvre des contextes distincts. Un exemple de cas d’usage est l’étude des ventes d’un magasin en période de soldes et le reste de l’année.
Travailler sur ces méthodes nous a permis de consolider notre approche pour traiter le sujet et de nous approprier des méthodes pouvant facilement transporter les données d’un contexte vers un autre, et ce de façon bidirectionnelle.
