Techniques d’intelligibilité en Deep Learning appliquées à l’image
✍ Bastien Roussel et Michaël Sok / Temps de lecture : 20 min
L’enjeu de l’intelligibilité d’un modèle de deep learning est double. Lors de sa conception par le data scientist, la compréhension de l’origine des biais du modèle permet de les corriger et ainsi d’atteindre de meilleures performances mais aussi de le rendre plus robuste. La compréhension du comportement du modèle permet aussi une meilleure acceptation par les métiers qui s’appuient sur ses résultats dans le cadre de leurs activités. Cet article a pour vocation de présenter les principales méthodes existantes pour interpréter des modèles de deep learning appliqués à l’image.
Les techniques de base en intelligibilité des modèles de deep learning
On peut distinguer deux grandes familles de techniques d’intelligibilité des modèles de deep learning.
Les techniques de forward propagation : basées sur des calculs de proche en proche depuis l’entrée vers la sortie du réseau neuronal
En faisant varier chaque entrée indépendamment et en calculant l’impact de cette nouvelle valeur sur la sortie on peut déterminer les entrées qui ont le plus d’importance sur la sortie.
Ces méthodes sont très intuitives dans leurs approches mais présentent de sérieuses limites. En outre, leur coût en calculs est très élevé puisqu’une forward propagation doit être calculée pour chaque entrée et pour chaque valeur à tester. Elles sont aussi susceptibles de sous-estimer l’importance de certaines entrées qui par leurs contributions saturent la sortie du modèle.
Pour illustrer le problème de saturation, prenons l’exemple d’un réseau composé de deux entrées i_{1} et i_{2}, d’une couche intermédiaire notée h et d’une couche de sortie y comme décrit ci-dessous :
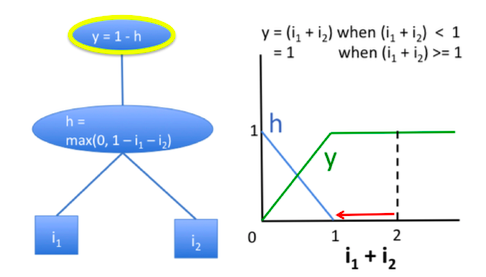
Source : Article de DeepLIFT
On remarque que tant que la somme de i_{1} et i_{2} est supérieure à 1 la sortie vaut 1. Par conséquent, si on fixe i_{1}=1 et qu’on fait varier i_{2} de 1 à 0, la sortie sera insensible à cette perturbation. Pourtant, il est clair que i_{1} a autant d’importance que i_{2}.
Les techniques de backpropagation : basées sur des calculs de proche en proche depuis la sortie vers l’entrée du réseau neuronal
Ces techniques sont beaucoup plus efficientes en terme de calcul puisque l’ensemble des contributions des entrées sont calculées en une seule passe à travers le réseau.
Une technique classique consiste à calculer la variation de la sortie au voisinage de l’entrée pour chacune de ses dimensions. Pour cela le gradient de la couche de sortie est exprimé en fonction de chaque dimension de l’entrée. Ce calcul est réalisé de proche en proche de la manière suivante :
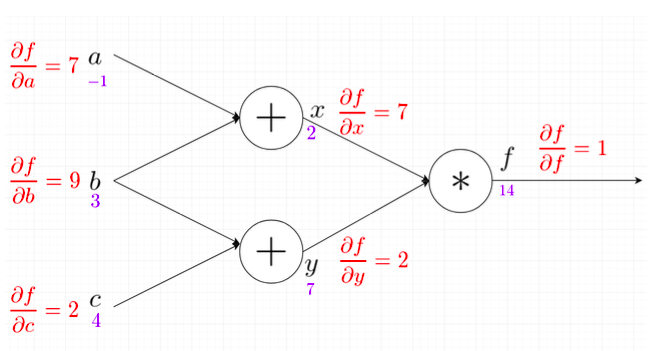
Source : article medium [4]
D’après le principe de dérivation en chaîne on peut calculer la pente de f dans chacune des 3 dimensions de l’entrée au voisinage considéré. Dans ce cas, la dimension d’entrée qui a la plus grande importance sur la sortie est b.
Bien que ces techniques soient beaucoup moins coûteuses en calculs, elles présentent encore des limites importantes :
- Le problème de saturation vue plus haut n’est pas résolu.
- La nature discontinue du gradient peut mener à des scores d’importances qui ne traduisent pas le changement infinitésimal de la sortie.
- Elles décrivent seulement le comportement local au voisinage d’une entrée qui peut ne pas être représentatif de l’ensemble du dataset.
Des méthodes plus élaborées adressent les trois limites rencontrées plus haut.
La méthode avancée des gradients intégrés
La méthode des Gradients Intégrés consiste à attribuer à chaque input un score d’importance basé sur la moyenne des gradients calculés en plusieurs points d’interpolations. Ces points d’interpolations sont définis à intervalles réguliers entre une image choisie comme référence et l’image réelle qu’on a prise en input. Il est courant de choisir comme référence un fond noir ou une image bruitée.
Dans l’exemple ci-dessous, on part d’une image noire, on l’éclaircit jusqu’à voir nettement le pont de l’image originale.
Pour chacune de ces images on calcule le gradient pour chaque pixel. Plus la valeur de la dérivée locale est grande en un pixel et plus celui-ci apparaît lumineux dans la série d’image ci-dessous.
Finalement, les valeurs des gradients sont moyennées ou sommées pour obtenir une contribution relative de chaque pixel. Les pixels ayant le plus contribué à la classification sont ceux qui sont le plus lumineux dans l’image ci-dessus.
À noter, que puisque la méthode nécessite un calcul du gradient en plusieurs points cela implique un coût de calcul important.
La méthode avancée DeepLift
DeepLift cherche à expliquer la différence en sortie entre l’input réel et un input de référence en attribuant une contribution à chaque pixel de l’input réel. Ces contributions sont également calculées par backpropagation à l’instar du gradient.
Contrairement au gradient qui calcule une pente locale, DeepLift calcule une pente entre l’input réel et un input de référence (notée baseline) :
\frac{\partial F}{\partial x} = \frac{\partial Y}{\partial x} \frac{\partial F}{\partial Y} \rightarrow \frac{\Delta F}{\Delta x} = \frac{\Delta Y}{\Delta F} \frac{\Delta F}{\Delta Y}
slope = \frac{y-y^{baseline}}{x-x^{baseline}} = \frac{\Delta y}{\Delta x}
L’avantage de cette méthode est qu’elle ne nécessite qu’une seule passe à travers le réseau pour calculer les différentes contributions des pixels d’entrée.
Les méthodes du framework SHAP
Le framework SHAP propose notamment deux méthodes, implémentées notamment en python, qui dérivent l’une des gradients intégrés et l’autre de DeepLift.
SHAP calcul des contributions à la prédiction finale pour chaque pixel de l’image d’entrée ou bien chaque pixel d’une couche caractéristique. Le principe sous-jacent est issu de la théorie des jeux en coopération où le problème est de savoir comment redistribuer équitablement le gain entre les membres d’une équipe selon leur contribution. La formule de Shapley permet de répondre à ce problème.
GradientExplainer
GradientExplainer combine plusieurs idées issues des Gradients Intégrés, de la théorie de SHAP et du SmoothGrad. La technique se base sur l’espérance du gradient pour expliquer les contributions de chaque pixel. Les calculs de l’espérance du gradient pour chaque pixel d’entrée donne une bonne approximation de la valeur de Shap.
Pour calculer l’espérance du gradient en chaque pixel de l’image d’entrée on se donne un jeu de données de référence. La méthode sélectionne 200 images aléatoirement avec remise parmi ce jeu de référence. Pour chacune des 200 images précédemment tirées, une interpolation uniforme est calculée entre l’image de référence et l’input dont on cherche à déterminer les contributions par pixel. La méthode varie de celle des gradients intégrés puisque la valeur moyenne du gradient est calculée à partir d’images interpolées issues de différentes images de références. La valeur moyenne du gradient ainsi obtenue en chaque pixel est une approximation de la contribution de ceux-ci.
GradientExplainer offre la possibilité d’utiliser un paramètre supplémentaire appelé le local smoothing qui permet d’ajouter un bruit gaussien à l’input avant de calculer les interpolations.
L’illustration ci-dessous est un exemple de ce qu’on peut obtenir en sortie de GradientExplainer. Dans le cas présent, les valeurs de shap ont été calculées relativement à 2 classes. Les pixels rouges représentent les pixels qui contribuent à augmenter la probabilité de l’image d’appartenir à cette classe. Inversement les pixels bleus représentent des valeurs de shap négatives.
DeepExplainer
DeepExplainer est basé sur le même principe que DeepLift. Il diffère néanmoins de DeepLift puisqu’il utilise une série d’images de références pour estimer les valeurs de shap.
Cette fois-ci les valeurs de Shap sont estimées en moyennant les pentes calculées entre l’input d’entrée et les différentes valeurs de références choisies.
A noter, plus on prend de valeurs de références et plus l’estimation est précise en revanche le temps de calcul augmente.
L’affichage des résultats est similaire à GradientExplainer.
Les autres méthodes existantes
Comme indiqué dans la section 1 de cet article, d’autres méthodes d’intelligibilité existent, reposant principalement sur de la backpropagation ou de la forward propagation plus classique.
Activation Layers Visualisation (Visualisation des Couches d’Activations)
Cette méthode d’intelligibilité, est la plus intuitive au sens de réseaux de neurones convolutifs. En effet, si l’on revient à l’essence même de la convolution, cela revient à calculer une somme pondérée de pixels dans un voisinage en suivant un certain noyau. Ces noyaux permettent par exemple de faire de la détection de contours (edge detection) avec des filtres ignorant certains axes. Par exemple, le noyau
permet de chercher les contours suivant l’axe diagonal haut-gauche/bas-droite.
L’objectif du réseau est donc d’entraîner les poids des noyaux de convolution pour ressortir des caractéristiques de l’image pouvant servir à accomplir la tâche, par exemple de la classification d’images.
L’idée sous jacente de la visualisation des couches d’activations est donc finalement de faire une forward propagation d’une image en input, et de s’intéresser à l’activation des convolutions dans une des couches intermédiaires du réseau [4]. Certaines caractéristiques devraient donc ressortir spécifique à l’image, typiquement les contours de l’objet à classifier par exemple, si l’on fait passer l’image d’un Jarret rouge (un certain type d’oiseau) dans un modèle VGG-16 (Keras, TensorFlow backend) et que l’on s’intéresse à la 7ème couche du modèle (couche de convolution d’entrée du 3ème bloc du VGG-16), nous pouvons obtenir la visualisation de l’activation de la convolution sur son premier filtre :
Il est bien sûr conseillé de le faire sur tous les filtres de la convolution, certains étant plus activés que d’autres, ou spécialisés dans certaines caractéristiques :
Dans cette image, nous remarquons effectivement que les différents filtres, peuvent se focaliser sur différentes parties de l’image (le bec de l’oiseau, le paysage, le corps de l’oiseau etc.). Une méthode pour trouver des filtres pertinents serait de regarder les activations maximales.
Occlusion Sensitivity (Sensibilité à l’Occultation)
Cette deuxième méthode est elle aussi très intuitive. L’objectif derrière cette méthode est de cacher une partie de l’image et de voir la modification dans la prédiction du modèle (avec une forward propagation) [4]. Ceci est itéré avec plusieurs parties différentes de l’image puis on moyenne les résultats sur les zones étant occultées plusieurs fois (si la zone n’est pas un unique pixel par exemple). Comme son nom l’indique, cette méthode s’inscrit dans de l’analyse de sensibilité.
Dans un cas pratique, nous pouvons voir la méthode de sensibilité à l’occultation sur le même Jarret Rouge que précédemment :
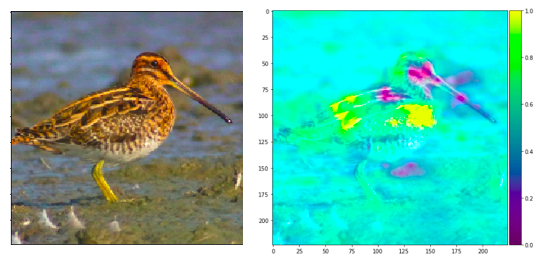Nous voyons donc qu’avec cette méthode, les pixels qui, occultés, apportent la plus grande diminution dans la prédiction sont ceux au niveau du corps de l’animal, alors que ceux proche du bec de l’animal apportent une amélioration. Nous remarquons que l’explication de la prédiction à travers cette méthode est que l’oiseau est classé comme un Jarret Rouge grâce à son corps (son poitrail est ses plumes), tandis que sa tête est son bec apporte une diminution de confiance dans la prédiction. Dès lors, il pourrait être intéressant de comparer les résultats avec l’avis d’un expert pour voir si le modèle se base sur des features pertinentes ou non pour effectuer sa prédiction.
Smooth Grad
La méthode d’intelligibilité Smooth Grad [5] est très similaire à une méthode de sensibilité classique, à savoir calculer la dérivée partielle de l’output de la fonction de prédiction par rapport à une input donnée (un pixel en l’occurrence). Cependant, dans cette méthode, il n’est pas question de ne s’intéresser qu’à la carte de sensibilité d’origine mais à une moyenne de plusieurs cartes de sensibilité associée à l’image bruitée avec un bruit gaussien centré de variance donné en hyperparamètre.
L’intuition derrière cette méthode provient du fait qu’un pixel (resp. une zone) important (resp. importante) pour la prédiction devrait le rester dans un voisinage proche.
De cette manière, sur notre oiseau préféré, nous pouvons observer l’évolution de la carte de sensibilité :
Comme indiqué dans l’article d’origine [5], le paramètre noise se définit comme :
noise = \frac{\sigma }{^{x_{max}-x_{min}}}
où σ est l’écart type du bruit gaussien utilisé, x_{max} la valeur maximale des pixels de l’image (prétraitée) et x_{min} la valeur minimale.
Nous remarquons donc ici que plus le bruit s’accentue, plus les pixels ayant une forte sensibilité sont ceux centrés autour du corps de l’oiseau (sa silhouette se dessine avec un bruit à 5 ou 10%). Bien sûr, quand le bruit devient trop fort, la carte de sensibilité ne sera plus pertinente (bruits à 20 à 50% par exemple ici).
Grad CAM
Grad CAM est l’acronyme de Grad(ient-weighted) Class Activation Map [6]. Son nom indique ainsi que l’output de cette méthode est une carte d’activation dépendante de la classe. L’objectif de cette méthode est de faire une forward propagation de l’image jusqu’au score brut de la catégorie (avant l’activation softmax). Ensuite une backpropagation est effectuée sur un vecteur de gradient one-hot de la classe prédéfinie, jusqu’à la couche de convolution qui nous intéresse où les gradients seront moyennés par Global Average Pooling pour obtenir un vecteur de poids a_{k}. Une somme pondérée de ces derniers avec les outputs de la convolution qui traverse ensuite une fonction d’activation ReLU permet d’obtenir la carte d’activation de la classe :
GradCAM = \sum_{k}a_{k}A_{k}
avec A_{k} l’output de la couche de convolution donnée.
Une variante existe (et c’est celle que TensorFlow implémente) appelée Guided-Grad CAM consiste à ne s’intéresser qu’aux gradients positifs ainsi qu’aux valeurs de la convolution qui sont positives pour guider l’explication vers les centres d’intérêts de la prédiction.
Sur notre exemple préféré, vous pouvez voir la Guided-Grad CAM sur les différentes couches de convolution de VGG-16 :
Nous pouvons remarquer que dans la dernière couche de convolution, les features utilisées pour la prédiction étaient celles du corps de l’animal, et en remontant dans les couches, certains pixels d’importance se dessinaient sur les features de l’animal !
Bibliographie
[1] https://towardsdatascience.com/interpretable-neural-networks-45ac8aa91411
[2]https://medium.com/@kartikeyabhardwaj98/integrated-gradients-for-deep-neural-networks-c114e3968eae
[3] https://arxiv.org/pdf/1704.02685.pdf
[4] https://medium.com/spidernitt/breaking-down-neural-networks-an-intuitive-approach-to-backpropagation-3b2ff958794c
