Défis et enjeux de la modélisation spatio-temporelle.

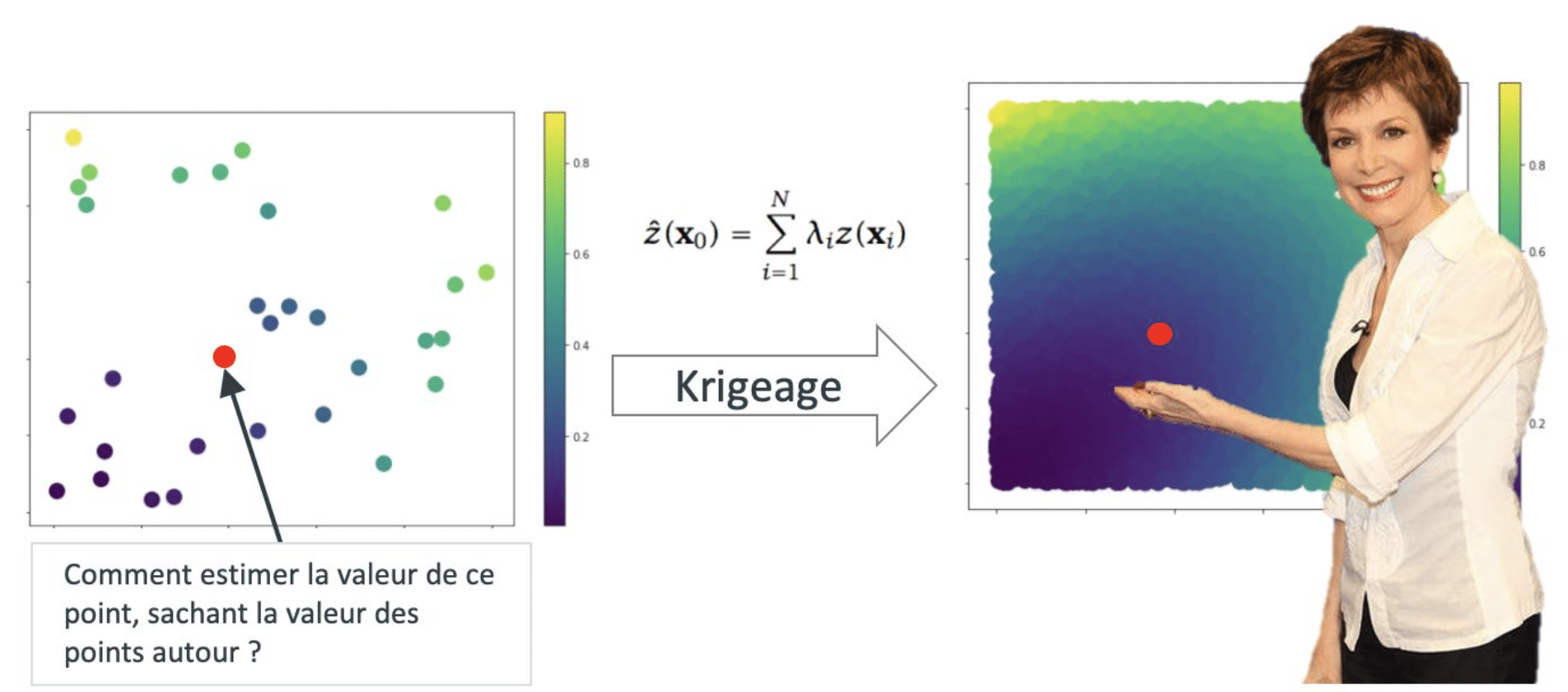
Le traitement de l’information géolocalisée n’est pas récent. La géostatistique naît dans les années 1950 en Afrique du Sud, grâce aux travaux de Danie G. Krige alors ingénieur minier. Le français Georges Matheron formalise les travaux de Krige à partir des années 1960 et consacre sa vie aux géostatistiques. On lui doit notamment le Krigeage (Kriging en anglais), une méthode d’interpolation spatiale utilisée en géologie, climatologie ou en encore météorologie. 

Cependant, à l’ère du tout numérique, l’information géolocalisée n’échappe pas au Big Data, que ce soit en termes de diversité de source ou de volumétrie. La technologie, via nos smartphones, est devenue une interface naturelle à notre monde, en s’y confondant presque. Nos usages changent, et nos outils parlent, décrivant nos comportements d’une manière de plus en plus précise.

Dans cet article nous répondrons à plusieurs questions :

• Pourquoi le Big Data est un frein au traitement de l’information géolocalisée ?
• Existe-t-il un continuum du deep learning à la modélisation spatiale et spatio-temporelle ?
• Les pistes prometteuses pour faire de la géostatistique at scale. 

Pourquoi le Big Data est un frein au traitement de l’information géolocalisée ? 

Les méthodes développées jusqu’alors ne passent pas à l’échelle du Big Data, tout simplement. A l’instar des séries temporelles, les méthodes usuelles de géostatistiques viennent s’appuyer sur une analyse des autocorrélations spatiales. Ce qui signifie simplement que lorsque l’on fait des mesures (une température par exemple), elles sont toutes plus ou moins liées entre elles. L’intensité de leur liaison est bien souvent fonction de la distance qui les séparent les unes des autres. 

Dans une ressource de l’INSEE, Bouayad Agha Salima et Marie-Pierre de Bellefon donnent la définition suivante à la notion d’autocorrélation spatiale :

Les indices d’autocorrélation spatiale permettent de mesurer la dépendance spatiale entre les valeurs d’une même variable en différents endroits de l’espace. Plus les valeurs des observations sont influencées par les valeurs des observations qui leur sont géographiquement proches, plus l’autocorrélation spatiale est élevée.

Il y a deux différences majeures avec les séries temporelles :

1. L’autocorrélation temporelle est unidirectionnelle (passé, présent, futur), quand l’autocorrélation spatiale est omnidirectionnelle (pour un point donné, les autres points sont distribués à 360° degré autour de lui, et à des distances qui varient).
2. Le temps est traité généralement de manière discrète, alors que l’espace peut souvent être traité de manière continue.

Ces deux différences suffisent à rendre quasiment inaccessible les méthodes de traitement des données géolocalisées quand le volume de donnée à traiter est élevé, puisque la complexité algorithmique de la plupart des méthodes exactes est de Ο(n3), ou n est le nombre d’observations. On observe aussi un changement de paradigme : le Krigeage a été initialement développé dans un contexte où le nombre d’observation était faible et où le coût d’acquisition d’une nouvelle observation était élevé (temps, argent), c’est le cas des sondages miniers par exemple. Une volumétrie élevée n’était pas nécessairement le goulot d’étranglement. Aujourd’hui la situation est inversée pour bon nombre de cas d’usage autour de la donnée géolocalisée : le nombre d’observation peut être très élevé, pour un coût d’acquisition faible. 

Nous ne détaillerons pas les approches usuelles de modélisation spatiale, mais vous pouvez trouver d’excellentes ressources si la formalisation mathématique de ces méthodes vous intrigue :

• Introduction to geostatistics, Geoff BOHLING
• An introduction to spatial econometrics, James P.LESAGE

Que vient faire le Deep Learning dans tout ça ?

L’apprentissage profond est basé sur des réseaux de neurones artificiels. Le concept n’est pas nouveau, puisqu’il date des années 1980, mais pour autant l’utilisation massive d’architectures de réseaux de neurones de plus en plus complexes est relativement récente, et est devenue possible grâce à des ordinateurs plus puissants, et une donnée disponible en masse pour entraîner de tels algorithmes. Le deep learning a révolutionné l’intelligence artificielle, en s’attaquant avec succès à des sujets de vision par ordinateur (reconnaissance d’image, détection d’objets, segmentation), de traitement du langage (détection de sentiments, extraction d’entités nommées et labellisation de texte, traduction), de traitement audio (classification de son, speech to text, génération automatique de musique). 

Pour vulgariser, un ensemble de traitement successifs, et adaptés à la nature de l’information traitée en entrée permet de créer une abstraction profonde. Parmi les grandes familles de « couches » (car c’est comme ça qu’on appelle ces traitements successifs) on retient celles qui permettent de traiter des images, par le biais de convolutions, et celles permettant de traiter des séquences (du texte, des séries temporelles), Long Short-Term Memory (LSTM) et Gated Recurrent Unit (GRU) étant les plus notables. Comme il est possible de combiner ces couches, tous les ingrédients sont réunis pour traiter de l’information spatiale (grâce à la convolution) et de l’information temporelle (traitement d’une séquence). 

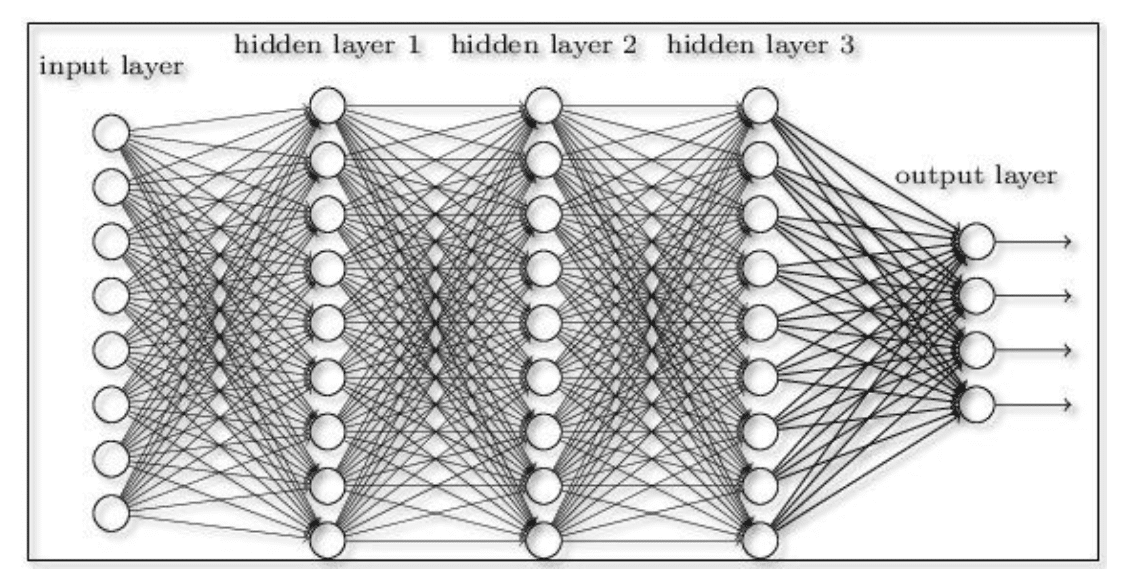
Vision d’un réseau de neurone (fully connected). A gauche les entrées (donnée brutes) et à droite les sorties (ce qu’on essaie d’estimer). Les couches intermédiaires sont dites “cachées”. Il s’agit dans ce cas de couches denses, mais il peut s’agir de convolutions ou de LSTM par exemple.

Ainsi, si le domaine des  séries temporelles a été sérieusement abordé par le Deep Learning, l’information spatiale est pour le moment restée assez inexplorée, et aucun standard d’architecture n’a été adopté par la communauté. Les nouvelles problématiques de mobilité liées au smart cities, et le développement de nouvelles offres de service (autopartage, vélos et trottinettes en libre-service) créent un terrain fertile à la recherche et l’expérimentation de nouveaux algorithmes de Deep Learning, en partie grâce à la volumétrie de donnée générée et à la naissance de tous nouveaux cas d’usage.

Dans la littérature récente, une architecture a retenu notre attention : Spatial-Temporal Dynamic Network (STDN), proposée par Huaxiu Yao, Xianfeng Tang, Hua Wei, Guanjie Zheng,  et Zhenhui Li de Pennsylvania State University, en mars 2018. Le papier est intéressant d’une part parce que l’approche est originale, qu’elle est testée sur un jeu de données régulièrement utilisé par la communauté scientifique (NYC Taxi),  que le code est disponible sur Github, donc reproductible, et qu’enfin l’architecture est plutôt spécifique à une problématique de mobilité, qui constitue un des enjeux des prochaines décennies et sur lequel nous avons misé chez Quantmetry, en développant un programme R&D sur le sujet.

Le problème : 

• On observe des taxis, à New York
• On a des informations géolocalisées sur les départs, les arrivées et les dates associées à chacun de ces deux événements
• On souhaite faire des prévisions sur les arrivées et départs en fonction du temps et de la localisation

Regardons ce qui fait que cette architecture traite de manière originale le problème : 

• L’idée majeure est de discrétiser l’espace (la carte de New York) et de créer des zones sur lesquels les séries temporelles sont agrégées. Il y a ainsi autant de séries temporelles que de zones. Le traitement qui en découle est naturel :
• • il est possible de traiter la carte comme une image, où chaque zone représente un pixel et d’y appliquer une convolution. Les auteurs utilisent la convolution non pas directement sur la carte, mais sur un voisinage de chaque “case” représenté par deux matrices carrées, l’une comptabilisant les entrées de zones, l’autre les sorties

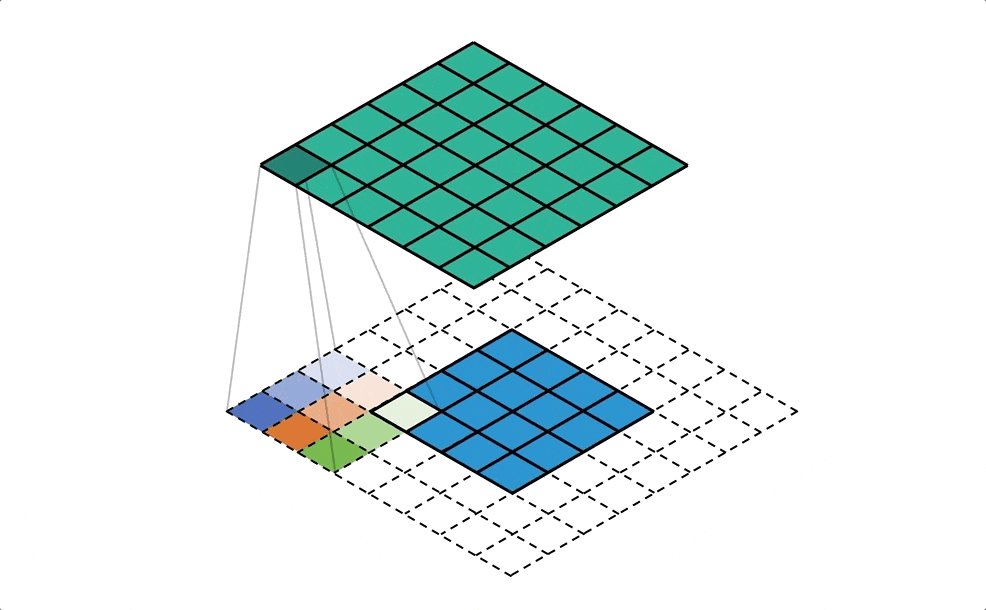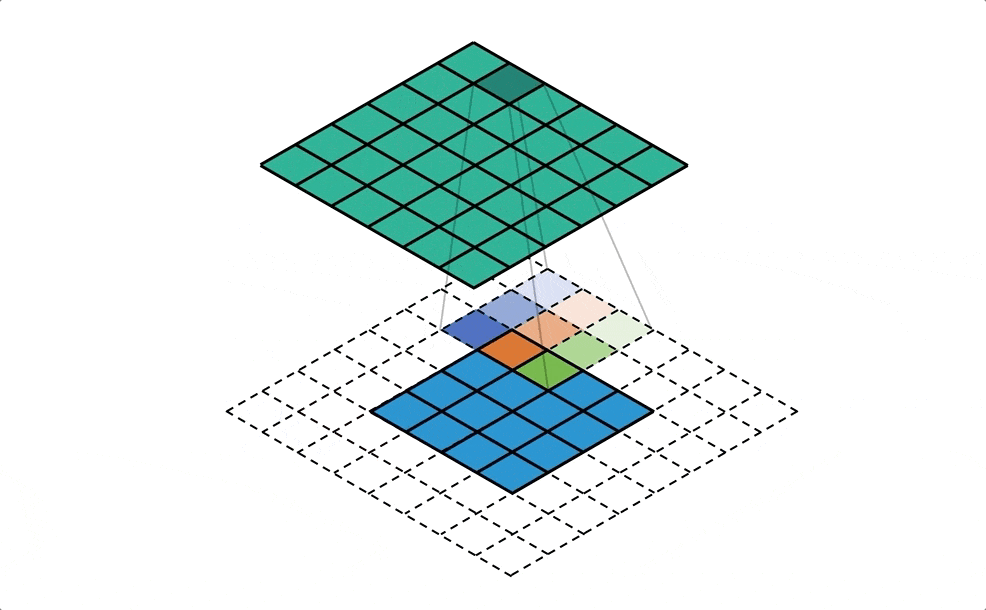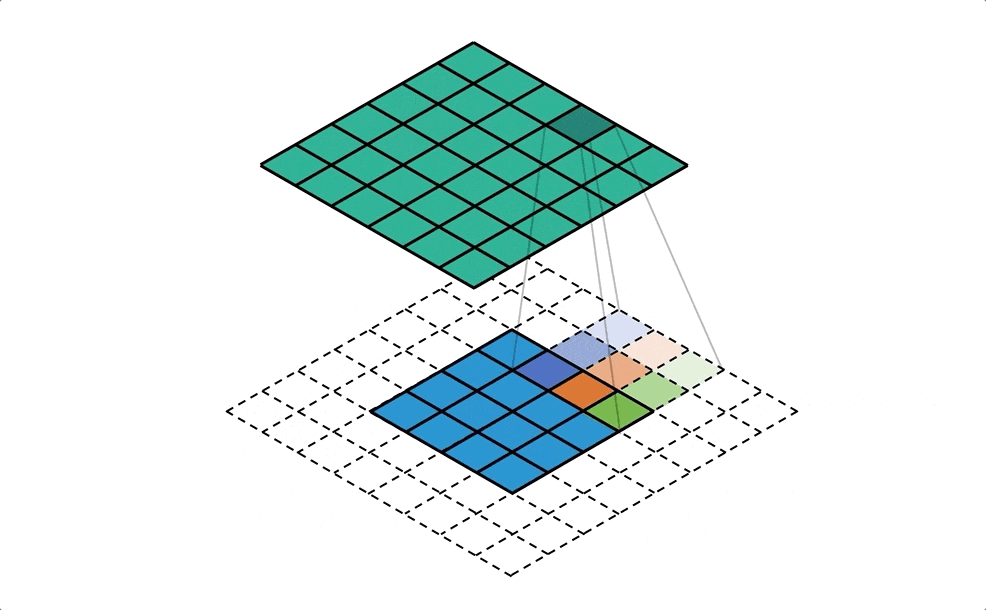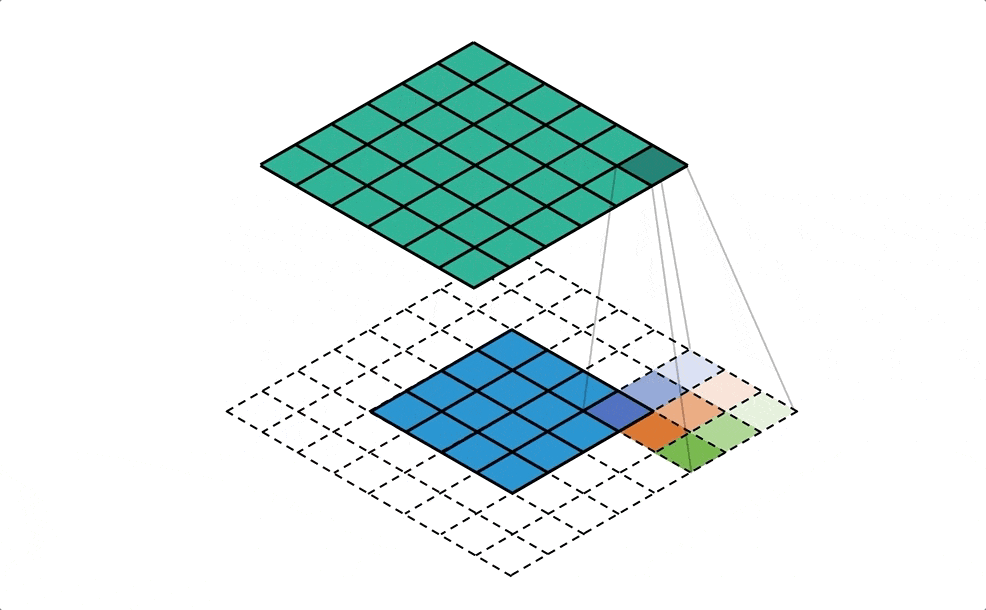
• • chaque série temporelle est traitée comme une séquence (utilisation de LSTM).

• • Les auteurs introduisent de plus le Flow Gating Mechanism (FGM), dont le but est de capturer explicitement de potentiels flux entre les zones. Il s’agit de travailler de nouveau sur un voisinage, mais de comptabiliser cette fois les flux sortants du voisinage pour rejoindre n’importe quelle autre zone qui n’est pas dans le voisinage, et inversement les flux entrants d’une zone quelconques externe au voisinage dans le voisinage. 
  • Enfin un mécanisme d’attention est utilisé pour capturer des dépendances long terme.

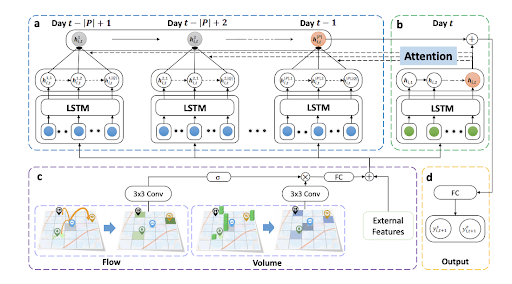
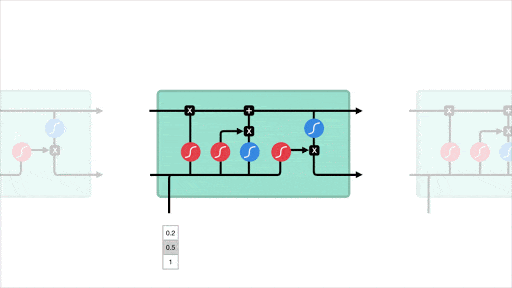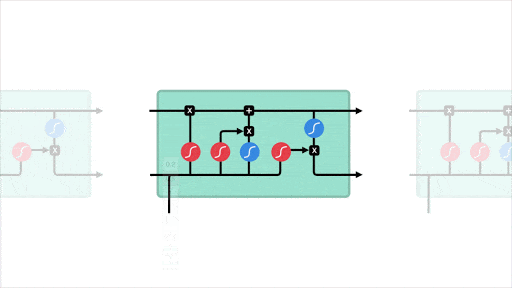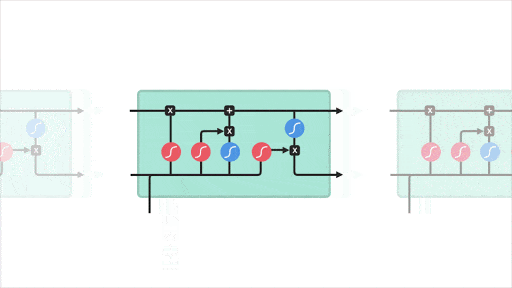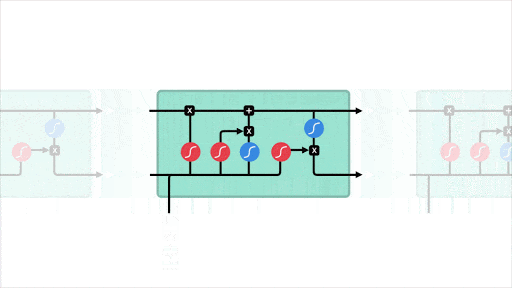
Architecture STDN : étude de voisinages par le biais de convolution, traitement de séquences via des couches LSTM, module d’attention pour traiter des dépendances court terme.

Le pré-traitement suivant est réalisé par les auteurs pour se contraindre à l’architecture du réseau de neurone :

• Division de la ville en une grille de 10×20
• La taille de chaque région est d’environ 1 km × 1 km
• L’information est agrégée à un pas de temps de 30min

Après entraînement de l’algorithme, les auteurs comparent leurs résultats à ceux d’autres algorithmes et montre que l’architecture STDN bat un grand nombre de méthodes (de la série temporelle classique, au deep learning en passant par du machine learning avec des modèles par arbres).

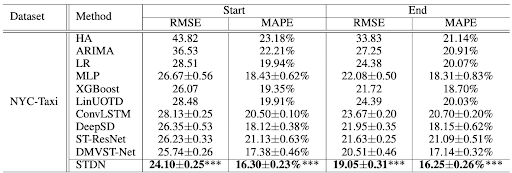
Scores extrait du papier : performance de STDN versus d’autres méthodes sur le jeu de donnée des taxis de New York.

Très synthétiquement, les auteurs ont eu un certain nombre d’idées plutôt classiques mais aussi assez astucieuses pour capturer des autocorrélation spatio-temporelles, et démontrent au passage, une fois de plus la flexibilité du deep learning.

Pourtant, il est légitime de s’interroger sur la pertinence des réseaux de neurones pour résoudre des tâches de cette complexité. Le papier démontre qu’il est possible d’utiliser des éléments déjà identifiés depuis longtemps pour construire une architecture qui permet de traiter ce type de problème. Il ne démontre pas cependant la supériorité du deep learning dans le traitement de la donnée géolocalisée, et ne propose nécessairement pas non plus de réponse à cet écueil qu’est le Big Data ici.

Enfin, et si un investissement en temps supplémentaire dans la compréhension du problème ne nous permettait pas de découvrir par nous-même ce que le réseau découvre pendant son entraînement ? La réponse au traitement de la donnée géolocalisée en volumétrie élevée n’est-il pas simplement entre la tradition et la modernité ? C’est en tout cas ce que semble montrer Uber dans le traitement des séries temporelles, par sa contribution à la fameuse compétition de time series M4 (retrouvez les grandes conclusions de cette compétition dans notre précédent article de blog ici) et l’hybridation d’un lissage exponentiel et de réseaux récurrents. 

Alors, n’y avait-t-il pas d’approche beaucoup plus simple ?

La réponse est oui, et voici une synthèse de la démarche : 

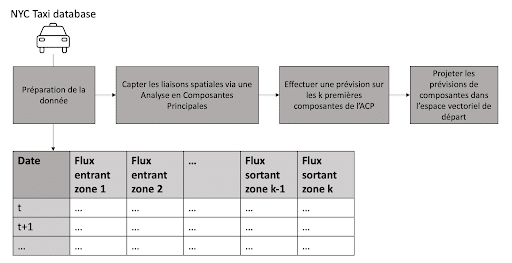
Concrètement, la démarche consiste à traiter dans un premier temps les autocorrélations spatiales par une analyse de la covariance entre chaque zone et type de flux (entrant ou sortant), via une Analyse en Composantes Principales. Ceci va créer des combinaisons linéaires de séries temporelles. Ensuite nous traitons les k premières composantes (celles renfermant le plus de variance) et construisant des modèles simples de prévision. Enfin il suffit de projeter les prévisions de l’espace des composantes dans l’espace initial, c-à-d spatial.

Et voici la démarche complète :

Tout d’abord, il est important de se plonger dans la donnée. Et l’on va voir qu’il ne faut pas beaucoup d’efforts pour comprendre l’essentiel du problème et simplifier son traitement : 

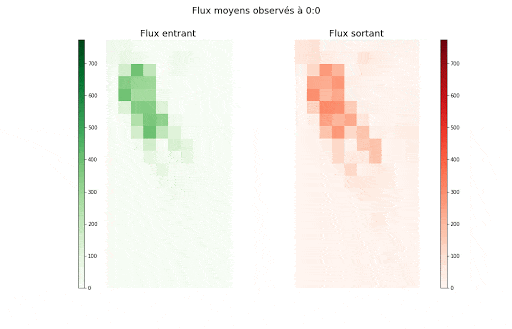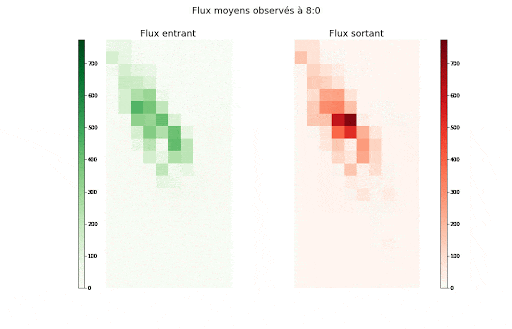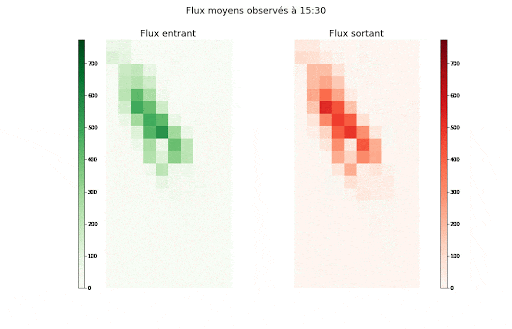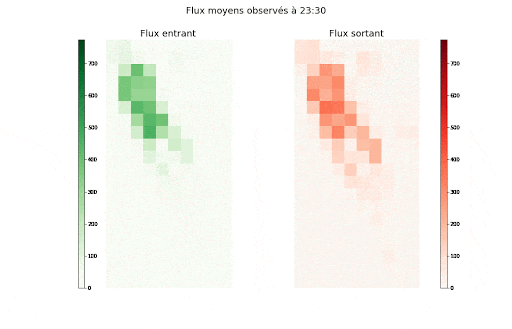
Valeurs des  flux entrants (vert) et sortants (rouge) moyens agrégés par demi-heure de la semaine et par zone

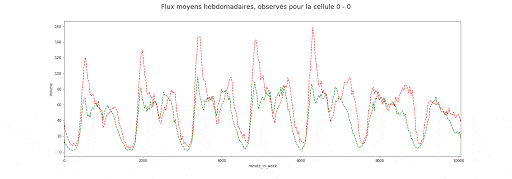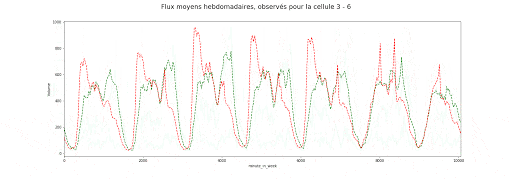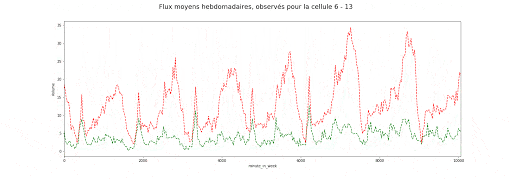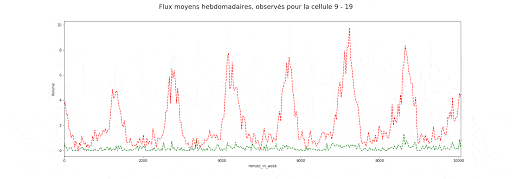
Valeurs des  flux entrants (vert) et sortants (rouge) moyens agrégés par zone et demi-heure de la semaine

Ces animations nous montrent deux éléments importants dans la manière dont est structurée l’autocorrélation spatio-temporelle, et dans la manière dont les flux entrants et sortants de chaque zone sont liés :

• Il y a d’une part, à la journée  voir semaine, une saisonnalité forte dont le motif peut varier en fonction de la cellule, c-à-d de l’emplacement discrétisé sur la carte de New York.
• Il y a aussi un lien étroit avec la dimension spatiale, puisque l’on observe un îlot où l’activité est bien plus forte qu’ailleurs.
• Enfin les flux entrants /sortants sont, pour une zone donnée, très corrélés entre eux, ce que montre la matrice suivante.

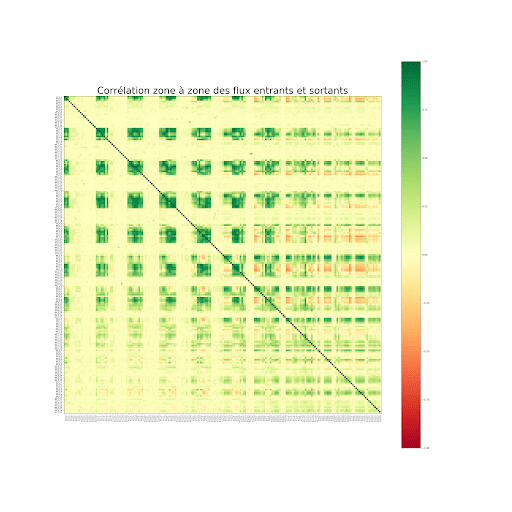
Corrélation zone à zone des flux entrants et sortants

En isolant les séries qui décrivent les flux entrants / sortants par zone, et en calculant le coefficient de corrélation de Pearson entre ces dernières, on remarque très rapidement que les séries sont localement corrélées entres elles (il s’agit des amas de corrélations de couleur verte foncée, ou rouge que l’on peut observer sur la matrice de corrélation ci-dessus). 

En s’inspirant du papier sur STDN, il devient ainsi très tentant de réaliser une analyse en composantes principale (ACP) afin de capturer des effets saisonniers dans différentes composantes. Si l’on intègre à la fois les flux entrants et sortants (qui sont très corrélés entre eux), et en faisant le lien avec l’article, on se rend compte qu’on est très proche de la philosophie du Flow Gating Mechanism et des opérations de convolutions effectuées sur la grille, puisqu’on peut simplement capturer avec ce type de décomposition naïve :

1. Des liaisons intra-zones entre des flux entrants et sortant dans la même zone.
2. Des liaisons inter-zones pour des flux entrants et sortants dans des zones différentes.
3. Des effets de saisonnalités temporelles locales, que ce soit pour des flux entrants ou sortants.

Il est aussi intéressant d’appuyer sur le fait que l’analyse en composante principale est la forme d’auto-encodeur la plus simple qu’on puisse trouver (une couche cachée avec une fonction d’activation linéaire), comme quoi les réseaux de neurones ne sont jamais loin. 

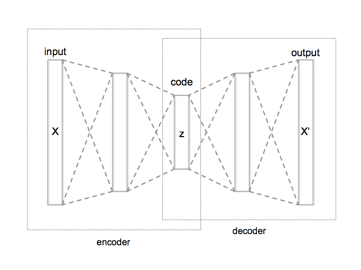
Vue macro d’un auto-encoder

En quelques mots, l’analyse en composante principale est une projection de notre donnée initiale (les séries ici en l’occurrence) dans un espace orthogonal. Ceci a pour effet de produire des séries décorrélées les unes des autres. Ainsi chaque série projetée (ou composante donc) doit, dans l’idée, capter un motif qui lui est propre.

Ceci est très simple à mettre en place : 

Ainsi chaque composante est une combinaison linéaire des flux.

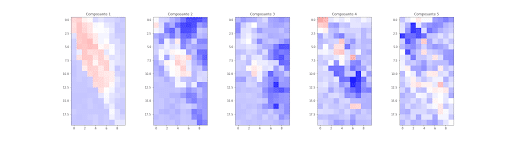
Contribution des zones dans les 5 premières composantes de l’ACP

En utilisant les vecteurs propres, et en calculant la contribution de chaque zone dans les 5 premières composantes, on observe ci-dessus que chaque nouvelle série temporelle issue de la projection orthogonale est associée à un ensemble de zones différent. Ceci signifie aussi que chaque composante capture un motif intrinsèque aux zones qui la décrive, comme elles sont décorrélées les unes des autres, et comme le montre les courbes ci dessous (les 5 premières composantes).

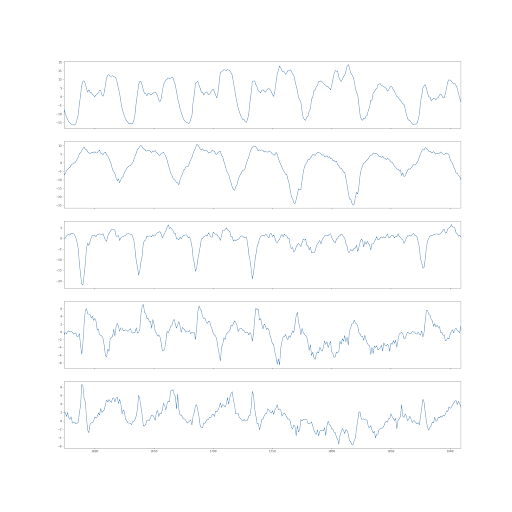
Composantes observées sous forme de séries temporelles

Maintenant que les différentes spécificités spatiales ont été isolées grâce à une ACP, il ne reste plus qu’à faire un forecast par composante. Il n’est sans doute pas nécessaire de faire un forecast pour toutes les composantes, puisque la variance totale captée pour une composante supplémentaire décroît avec le nombre de composantes. C’est ce que montre le graphique ci-dessous : déjà 20% de la variance totale est captée par la première composante, puis un peu moins de 15% pour la seconde composante. Si l’on ne fait pas un forecast sur toutes les composantes, cela signifie que dans la phase de reconstruction du signal initial, une partie (négligeable mais quantifiable) du signal sera perdue.

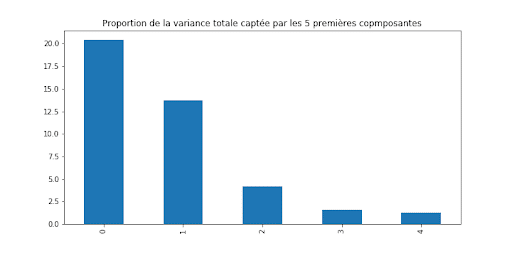
Variance captée par composante pour les 5 premières composantes.

La méthode de forecasting utilisée est finalement très simple. Il s’agit d’un triple lissage exponentiel (ou méthode Holt-Winters). C’est une méthode de lissage qui permet de tenir compte des différentes composantes d’un signal temporel, comme le niveau, la tendance, ou la saisonnalité. Une simple optimisation bayésienne des paramètres a été utilisée (via le package Python Hyperopt) pour déterminer rapidement les paramètres les plus adaptés au forecast de chaque composante. 

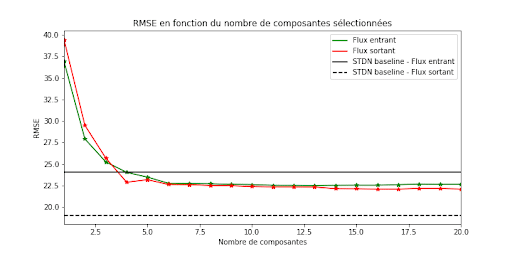
Si l’on étudie la RMSE, (c-à-d l’erreur quadratique moyenne) associée au nombre de composantes pour lesquelles on génère une prévision (20 ici) afin de reconstituer le signal initial, on observe qu’il suffit de seulement quatre composantes (sur 400 possibles en tout) pour battre le score atteint par STDN sur les flux entrants. En ce qui concerne les flux sortants, l’approche proposée ici ne bat pas STDN, mais s’en rapproche de manière sérieuse et bat une majorité des autres méthodes proposées dans le papier original (dont des architectures plutôt complexes de réseaux de neurones).

Il est enfin à noter que cette méthode est peu coûteuse en ressources mémoire / calcul, contrairement à un réseau de neurones où il faut optimiser un plus grand nombre de paramètres.

Quelles leçons doit-on tirer ?

• Souvent, comprendre le problème et être capable de traduire ses intuitions dans la phase de modélisation permet de réaliser une grosse partie du travail.
• Pour autant il est nécessaire de rester lucide face à la phase de modélisation, en gardant toujours en tête qu’une approche plus simple est aussi souvent une approche plus élégante.
• L’architecture STDN ne deviendra sans doute pas un standard pour traiter de la donnée géolocalisée, mais il y a beaucoup d’intuitions intéressantes à valoriser davantage.
• STDN ouvre le chant de la donnée géolocalisée et du deep learning.

Quelles pistes d’amélioration pour la méthode proposée ici ?

• Découper plus finement l’espace, en utilisant plutôt des carrées de 500m x 500m par exemple.
• Retravailler l’ACP, en utilisant un auto-encodeur plus complexe pour :
  • capter des relations non-linéaires (en jouant avec les fonction d’activation des couches, et le nombre de couches).
  • introduire une dimension temporelle dans l’auto-encodeur (LSTM par exemple), puisqu’ici l’analyse n’était basée que sur des comparaisons de zone à l’instant t (alors qu’on voudrait pouvoir comparer la zone A à t avec la zone B à t-3 par exemple).
• Utiliser une méthode de forecasting plus complexe et intégrant des variables externes. Si le nombre de composantes à estimer reste limité, il peut être intéressant d’utiliser des méthodes comme Prophet de Facebook ou de d’apprentissage automatique classique pour lesquels on peut introduire de l’information exogène (calendrier, météo).

Le deep learning pour la donnée géolocalisée ça ne donne rien alors ?

Si, et il y a plein d’approches très prometteuses. Et tout montre qu’effectivement, la réponse au traitement de la donnée géolocalisée en volumétrie élevée se situe actuellement entre la tradition et la modernité.

Elles se basent sur de nouvelles fonctions d’activations (approches géométriques par convolutions sur des graphs), ou de nouveaux types de réseaux (réseaux probabilistes, des processus gaussiens profonds). Ceci reste pour le moment assez expérimental, et il n’y a toujours pas d’architecture standard ou de Krigeage at scale. La communauté open source ne manque pas de ressources sur ces sujets. Je vous conseille de garder dans un coin de votre tête les projets suivants :

• GPyTorch, où comment faire tourner des processus gaussiens sur GPU.
• Pyro, où l’art de créer des réseaux probabilistes avec PyTorch et son homologue Tensorflow Probability. 
• PyTorch geometric pour faire du deep sur des graphs et des nuages de points.

Affaire à suivre…