Orienter sa stratégie de reprise grâce à l’optimisation sous contraintes

L’optimisation sous contraintes constitue un formidable levier d’aide à la décision, notamment intégrée dans des outils de S&OP dans un contexte de production industrielle, et plus généralement dans n’importe quel procédé de planification pouvant tirer profit d’une optimisation de l’allocation des ressources mises en jeu. Si en optimisation on modélise en général le comportement nominal, « normal » d’un système pour en optimiser son fonctionnement général, sa « fonction de coût », il est tout aussi possible d’optimiser une stratégie de reprise conséquente à un comportement nouveau, inhabituel. L’épidémie mondiale de COVID-19 et le confinement survenu à partir de mars 2020 en France illustre bien la nécessité d’adapter les outils de planification / d’optimisation à des situations inédites, pour mieux rebondir après la crise. Nous pouvons aussi dessiner un parallèle avec la nécessité de repenser / ré-entraîner les modèles prédictifs de machine learning : un modèle entraîné sur des données de 2018/2019 verra ses performances fortement dégradées au coeur du confinement, fin mars 2020!
Nous reprendrons pour détailler notre propos l’exemple de l’article suivant. Dans cette introduction à l’optimisation sous contraintes avec Pyomo, est développé le cas d’une société concentrée sur la production et la vente de vêtements. Cette société souhaite optimiser sa marge totale annuelle en respectant différentes contraintes métier, telle que la production maximale mensuelle.
Comme de nombreuses entreprises, ce secteur est touché de plein fouet par l’épidémie de COVID-19 : ses lignes de production ainsi que les points de vente ferment lors du confinement. L’heure du déconfinement a sonné, et les finances de l’entreprise ayant été durement impactées l’entreprise cherche plus que jamais à optimiser sa stratégie de reprise.
Problématique
La reprise des activités est officiellement prévue pour mi-mai, bien qu’un décalage soit possible. Soucieuse d’optimiser au mieux ses coûts de production, l’entreprise cherche alors à savoir à quel moment rouvrir ses ateliers d’assemblage. S’il paraît évident pour beaucoup qu’il faut rouvrir la ligne de production de T-shirt dès que possible (après de long mois confinés, la demande client sera sûrement bien plus forte que d’habitude), il se peut que la reprise économique prenne plus de temps que prévu. Et même si cette forte demande est au rendez-vous, le nombre de jour de production possibles du mois de mai est au mieux divisé par deux : le peu de jours de production disponibles pourrait ne pas être en mesure de suivre la demande. Il n’est pas sûr que la réouverture de la ligne de production de T-shirts soit intéressante financièrement. Ouvrir une ligne de production a un coût non négligeable, qu’il s’agit désormais de considérer!
Afin de répondre à cette problématique, la direction dresse différents scénarios de reprise. Deux scénarios sont jugés les plus probables :
- Le scénario numéro 1 table sur un déconfinement à la mi-mai. La demande commerciale est prévue relativement forte en mai, car les points de ventes ne sont ouverts que la moitié de la durée théorique du mois de mai
- Le scénario numéro 2 prévoit un éventuel décalage du déconfinement d’une semaine, à la dernière semaine de mai. Comme vous pouvez le voir dans le tableau ci-dessous, le nombre de jours ouvrés pour la production est alors réduit à 5.
Le tableau de données suivant est alors fourni à l’équipe d’optimisation, donnant pour chaque scénario la demande commerciale prévisionnelle et la capacité de production en nombre de jours de travail possibles :
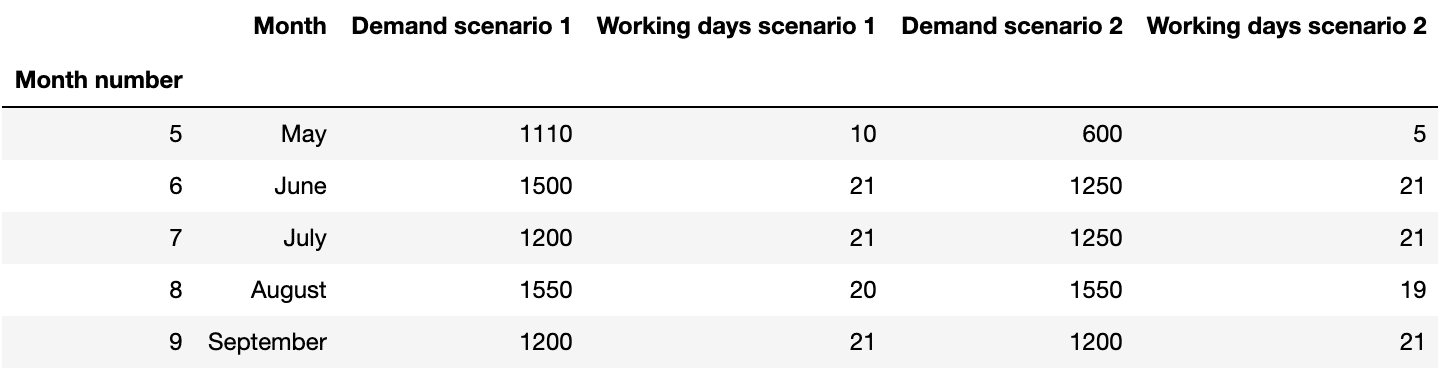
Demande client et nombre de jours ouvrés prévisionnels
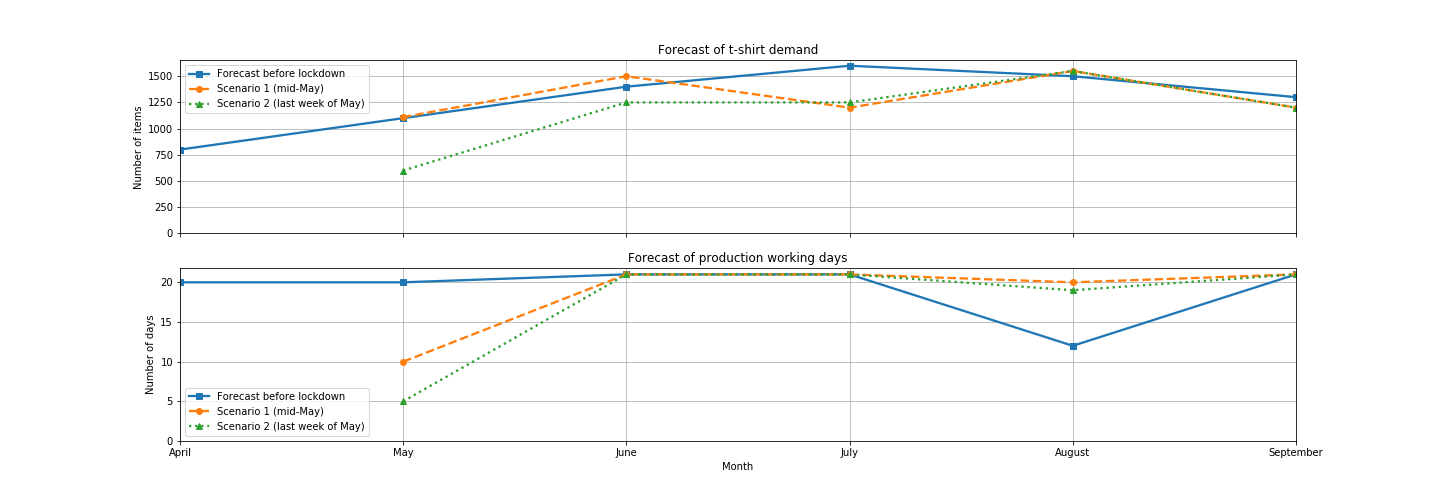
Illustration des données prévisionnelles pré et post-crise
Evolution du modèle d’optimisation
Si lors du développement du modèle initial, le besoin de prendre en compte les frais liés à l’activation des lignes de production n’avait pas été exprimé, il est désormais fondamental d’avoir cette information. En effet, pour pouvoir optimiser la stratégie de reprise d’un point de vue financier en activant ou non une ligne il faut que le modèle puisse prendre en considération ces frais d’activation. Comment allons-nous faire évoluer le modèle?
Création du modèle et index
La syntaxe de la création de modèle et de son index de variables ne change pas.
# Create model model = pyo.ConcreteModel(doc="Optimization model for production line reopening") # Create index for variables and parameters model.months = pyo.Set(initialize=(i for i in df.index), doc="Index of variables (months)")
Variables
Les variables d’optimisation définissant les ventes, les nombres de t-shirts produits et stockés en tant que nombres entiers non négatifs sont aussi conservées, à la différence que les variables de production ne sont plus bornées par des valeurs fixes dès leur instanciation, comme c’était le cas dans le modèle initial avec le paramètre bounds. Il est ici nécessaire de contraindre cette production avec trois notions : le nombre de jours, le quota et l’activation ou non de la production : nous verrons comment s’y prendre dans la définition des contraintes. Afin de considérer l’activation ou non de la ligne de production à chacun des mois du planning, la variable suivante est ajoutée au modèle. Remarquez l’utilisation de l’objet Pyomo Binary définissant le type booléen de la variable : chaque mois, la ligne sera ouverte ou non :
# New variable: activation status of production line model.activation = pyo.Var(model.months, domain=pyo.Binary, doc="Activation of production line")
Paramètres
Les paramètres du modèle initial définissant les coûts de production et prix de vente des t-shirts sont aussi conservés. Trois nouveaux paramètres permettent de définir le coût d’activation de la ligne de production, le quota de production (68 T-shirts produits par jour ouvré) et le nombre de jours de production. Remarquez la syntaxe de model.working_days. Comme pour la définition d’une variable à chaque mois de l’index, Pyomo permet de passer des valeurs issues de dictionnaires à des paramètres pour un écriture très concise :
# Existing parameters model.initial_stocks = pyo.Param(default=400, doc="Initial stocks") # New parameters model.activation_cost = pyo.Param(default=2000, doc="Activation cost of production line") model.quota_production = pyo.Param(default=68, doc="Produced items per working day") model.working_days = pyo.Param( model.months, initialize=df["Working days scenario 1"].to_dict(), doc="Number of working days per month" )
Fonction objective
Dans la fonction objective, un terme est ajouté pour considérer l’activation de la ligne de production et les coûts qui en découlent :
# Objective function def func_objective(model): objective_expr = sum([ (model.sales[v] * model.sale_price) - (model.productions[v] * model.prod_cost) - (model.stocks[v] * model.stock_cost) - (model.activation[v] * model.activation_cost) for v in model.months ]) return objective_expr model.objective = pyo.Objective( rule=func_objective, sense=pyo.maximize, doc="Objective function with activation costs" )
Contraintes
La contrainte initiale d’équilibre entre ventes, production et stocks ainsi que la contrainte de stocks sont conservées. Comme évoqué précédemment, nous devons imaginer une contrainte permettant de pallier la production en fonction du nombre de jours de travail, du quota et de l’activation de la ligne :
# New constraints list: take into account activation of production line each months model.constraint_activation = pyo.ConstraintList(doc="Production capacity") for m in model.months: model.constraint_activation.add( model.productions[m] <= model.working_days[m] * model.quota_production * model.activation[m] )
Une fois ce modèle finalisé, il est possible d’utiliser une nouvelle fois le solveur CBC, notre problème étant toujours linéaire. Le processus est facilement automatisable pour générer l’optimisation des volumes de ventes, productions, stocks et de l’activation de la ligne de production pour les différents scénarios en maximisant notre fonction objective model.objective. Une fois notre modèle correctement convergé, il est d’ailleurs possible d’obtenir la valeur finale de cette fonction de coût en appelant model.objective().
Résultats
Intéressons-nous à ce que recommande le modèle en ce qui concerne la réouverture de la ligne de production et la quantité produite selon les deux scénarios :
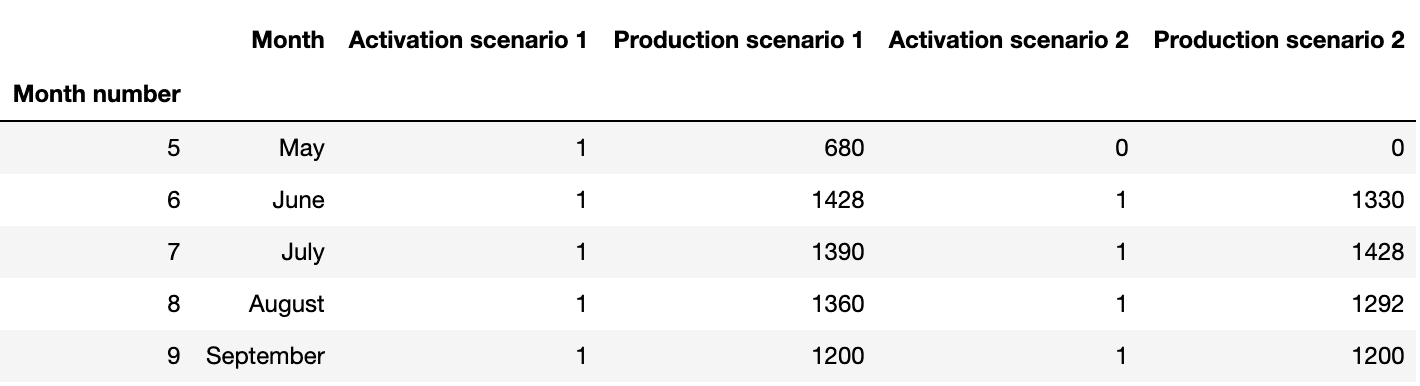
Résultats d’optimisation des différents scénarios
On peut voir que si pour le premier scénario de déconfinement à la mi-mai, le modèle préconise de bien réactiver la ligne dès que possible, ce n’est pas le cas du deuxième scénario. Avec une semaine seulement de production, il ne semble pas intéressant financièrement de payer les frais d’activation de la ligne. Analysons graphiquement cela en traçant l’évolution des volumes optimisés de ventes, production, stocks pour les deux scénarios :
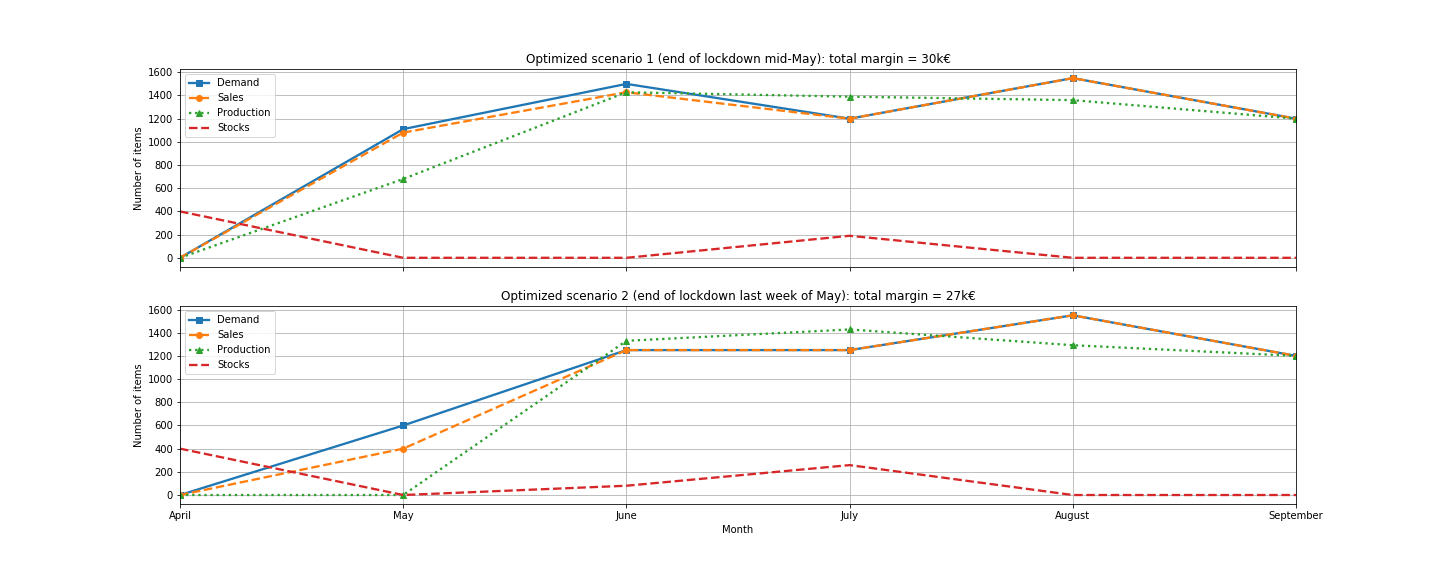
Comme vu précédemment, pour le scénario 1 l’optimiseur préconise de réactiver la ligne de production dès que possible : en produisant 680 t-shirts et en consommant l’ensemble des 400 en stocks il est possible de satisfaire la quasi-totalité de la demande.
Ce n’est pas le cas du scénario 2 : dans ce cas le modèle souligne qu’il est plus intéressant de ne satisfaire que les deux tiers de la demande prévisionnelle en s’appuyant uniquement sur les stocks. Réactiver la ligne de production pour la demande résiduelle impliquerait des surcoûts : avec des coûts d’activation de 2000€, les profits liés à la vente de 200 t-shirts (200 x 6€) entraîneraient une perte nette de 800€ ! Il est ainsi plus judicieux d’allouer les ressources de la ligne de production autre part.
Nous avons vu comment de simples modifications à un modèle d’optimisation permettent de le rendre réactif à une situation inédite. Il peut en effet représenter un support d’aide à la décision stratégique dans un scénario de crise entraînant l’arrêt de la production d’une entreprise. Notre exemple est simple et aurait pu être résolu par un calcul rapide. Mais quand le problème se complexifie, avec une multitude de produits et de lignes d’assemblages, des lignes d’assemblages dépendantes les unes des autres, ou bien encore des lignes produisant potentiellement plusieurs produits à la fois, la traduction du problème en un modèle d’optimisation représente un formidable levier d’aide à la décision.

