Solution au problème de routage des véhicules par programmation linéaire optimisée par l’apprentissage automatique

Motivation et contexte
Les problèmes d’optimisation d’itinéraire sont des problèmes difficiles à résoudre, principalement lorsqu’il s’agit d’instances de problèmes de taille réaliste. Dans sa forme la plus simple, le problème de tournées de véhicules (VRP) est un problème combinatoire consistant à desservir, de manière optimale et à partir d’un arrêt de dépôt fixe, un ensemble de clients avec une demande connue (e.g. temps de trajet) tout en minimisant le coût total.
La littérature en recherche opérationnelle (RO) couvre le VRP ainsi ses nombreuses variantes de manière approfondie depuis des décennies. Par conséquent, d’importants progrès ont été réalisés en ce qui concerne la qualité de la solution et le coût de calcul.
Néanmoins, il existe un écart entre la planification d’itinéraire théorique et l’exécution d’itinéraire réel. En effet, dans les opérations réelles, la qualité d’un itinéraire n’est pas exclusivement définie par sa longueur théorique, sa durée ou son coût. Il s’avère que les livreurs expérimentés ont une connaissance tacite de l’environnement dans lequel ils desservent quotidiennement. Par exemple, ils connaissent les heures de pointes de certains quartiers, les portions de routes moins roulantes, quand et où se garer facilement pour desservir plusieurs clients en même temps, etc. De telles informations sont difficiles, voire impossibles à formaliser dans un modèle d’optimisation et sont donc très rarement contenues dans la plupart des outils de planification d’itinéraires utilisé par les entreprises. En conséquence, les trajectoires initialement prévues ne sont jamais totalement suivies par les livreurs, préférant suivre un autre itinéraire potentiellement plus pratique dans des conditions opérationnelles réelles. Dès lors, essayer de comprendre et anticiper ces écarts afin de planifier des itinéraires plus efficaces, autant pour les livreurs que pour les clients, est un problème intéressant d’autant plus avec l’explosion de la livraison directe grand public (par exemple UPSground a livré environ 11,5 millions de colis en 1993 contre environ 5,5 milliards de colis en 2019, [1]).
Fin juillet 2021 se clôturait The Last Mile Routing Research Challenge, challenge organisé par Amazon et le MIT Center for Transportation and Logistics. L’objectif était de développer des approches innovantes tirant parti de l’intelligence artificielle, de l’apprentissage automatique et d’autres méthodes non conventionnelles pour produire des solutions au problème de séquençage d’itinéraires qui surpassent les méthodes de recherche opérationnelle traditionnelles axées sur l’optimisation en termes de qualité de la solution et coût de calcul. À partir de données réelles de demandes de livraison, les participants devaient générer, dans un laps de temps imparti, des séquences d’itinéraires qui fonctionnent « bien » suivant des mesures de performances imposées en apprenant à partir de séquences d’itinéraires réelles exploitées par de véritables conducteurs expérimentés.
Deux étudiants, co-supervisés par l’ENSIIE et Quantmetry, y ont participé et ont proposé une solution combinant programmation linéaire en nombres entiers et méthodes de machine learning au problème du « vendeur itinérant avec les fenêtres de temps » () avec un seul camion [3]. Plus précisément, le VRPTW constitue une généralisation du VRP dans la mesure où une contrainte temporelle sur le service demandé est ajoutée : chaque client dispose d’une fenêtre de temps à l’intérieur de laquelle il désire être servi.
Une tendance récente est d’appliquer des modèles de Machine Learning (ML) pour résoudre les problèmes d’optimisation combinatoire afin de trouver la séquence de routage étant donné un ensemble de données. La plupart des problèmes d’optimisation combinatoire, y compris le VRPTW, sont difficiles à résoudre, à la fois d’un point de vue théorique (NP-difficile) et d’un point de vue pratique (temps d’exécution exponentiel). Dès lors, des techniques de ML semblent être de bons candidats pour (tenter de) résoudre ces problèmes. Dans la suite, nous présentons la solution proposée ainsi que d’éventuelles futures directions.
L’approche adoptée
La résolution de ce problème se compose de différentes étapes illustrées dans la Figure 1. Tout d’abord, un programme linéaire (PL) en nombre entiers est défini. À l’instar d’autres approches d’optimisation, cette formulation ne peut résoudre efficacement des problèmes impliquant plus de 15 arrêts. Pour surmonter cette limitation, deux approches ML ainsi qu’un clustering sont utilisés. Cela permet de résoudre le problème initial plus facilement et plus rapidement.
Figure 1 : Aperçu de la méthodologie appliquée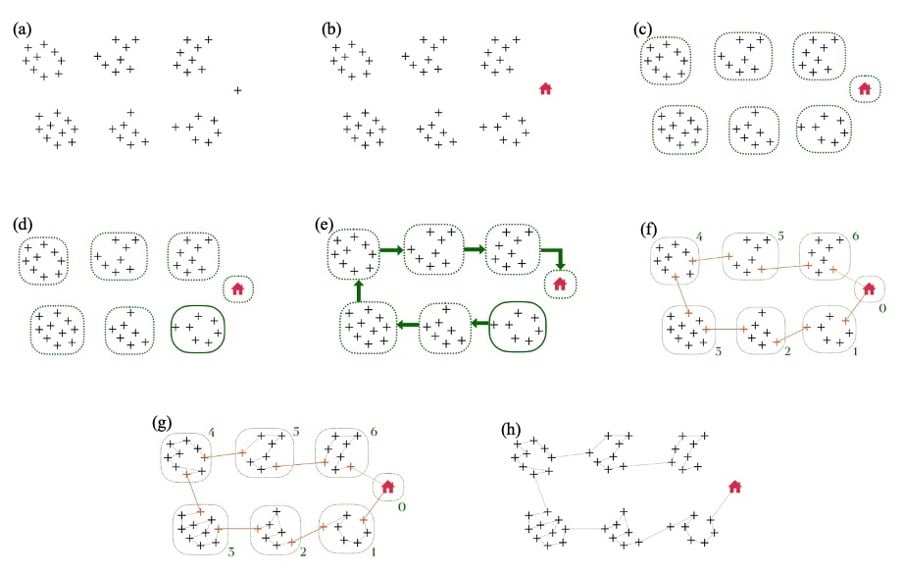
Figure 1. Aperçu de la méthodologie proposée [3]. (a) Soit un ensemble d’arrêts à desservir ; (b) on détermine le dépôt, identifiable par sa localisation ; (c) on regroupe les arrêts en zones puisqu’en général un livreur délivre tous les points d’une zone avant de passer à la suivante ; (d) on détermine la première zone à visiter au moyen d’une régression logistique; (e) on trouve une route reliant toutes les zone au moyen d’un programme linéaire ; (f) on détermine le premier et dernier arrêt dans chaque zone afin de relier physiquement les zones ; (g) à l’intérieur de chaque zone, connaissant les deux extrémités, le PL trouve une route reliant tous les points à délivrer ; (h) résultat final.
Dans le tableau ci-dessous, une description des données fournies par Amazon que nous avons utilisées pour la création de features de nos modèles de machine learning.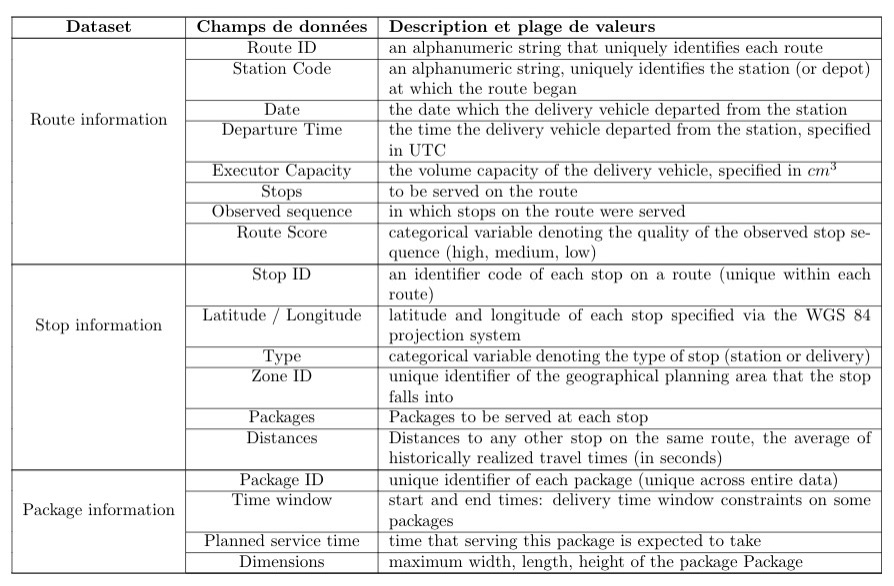
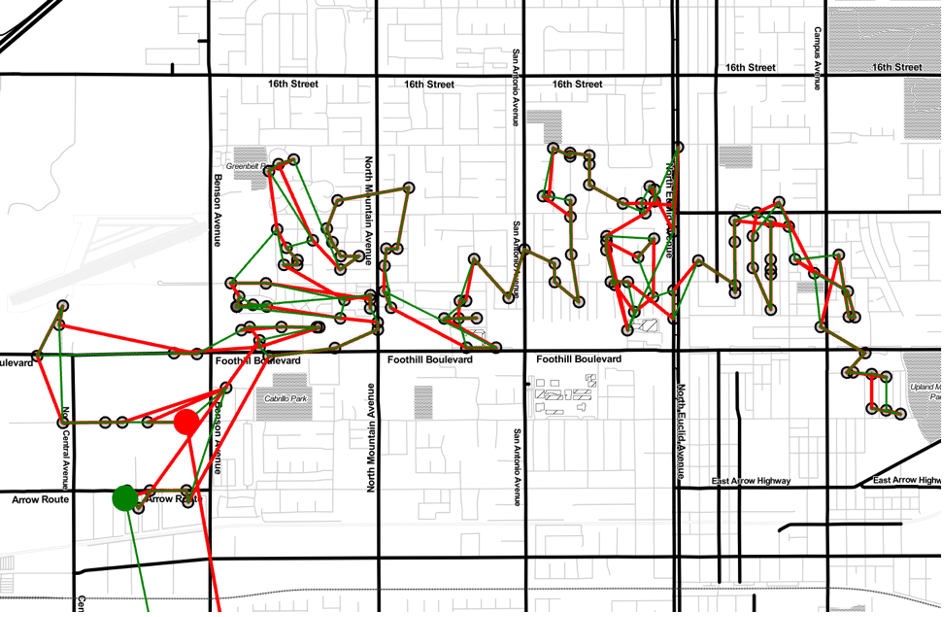
Figure 2 : Illustration de la solution trouvée.
La séquence rouge correspond à la route prédite et la séquence verte correspond quant à elle la route empruntée par un livreur. Les points de couleur pleins indiquent le premier arrêt effectué.
Formulation du problème
Quelques pistes d’amélioration
Voici deux pistes d’améliorations que nous souhaitons explorer pour améliorer la solution existante :
- Utiliser une nouvelle fonction objectif : si le problème ne peut être résolu uniquement par de l’optimisation, c’est parce que la fonction objectif n’est pas totalement connue. En effet, comme expliqué précédemment, il ne s’agit pas uniquement de minimiser le temps (ou distance) théorique de parcours du livreur mais de proposer une route proche de celle qu’aurait emprunté un bon chauffeur expérimenté. Dès lors, on peut espérer utiliser un modèle de machine learning pour approximer cette fonction inconnue.
- Améliorer la route post-optimisation : une fois une première route trouvée par un modèle d’optimisation et qui respecte donc l’ensemble des contraintes assurant sa faisabilité (par exemple le fait que tous les arrêts sont parcourus et que chaque arrêt n’est parcouru qu’une seule fois), il est possible d’effectuer des altérations locales de cette route sans altérer cette faisabilité. Les altérations à effectuer pourraient être prédites par un modèle de machine learning.
Références :
[1] Poullet, J. (2020). Leveraging Machine Learning to Solve the Vehicle Routing Problem with Tome Windows. PhD thesis, Massachusetts Institute of Technology.
[2] Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960°. Integer programming formulation of traveling salesman problems. Journal of the ACM (JACM), 7(4):326-329
[3] Winkenbach, Matthias; Parks, Steven; Noszek, Joseph Technical Proceedings of the Amazon Last Mile Routing Research Challenge
