Tout est graphe ! Détection de communautés : théorie et retour d’expérience

Après un premier article introductif à la théorie des graphes, notre série continue avec la détection de communautés. En effet, ce domaine offre de nombreux cas d’application (détection de fraude, RH analytics..) et la recherche y est florissante : dynamique temporelle des réseaux, multi-appartenance communautaire, métriques de performance… Cet article vise à donner une première vue d’ensemble des algorithmes et outils existants, ainsi qu’un retour sur leur utilisation pratique. Des illustrations seront également données à partir de données LinkedIn.

1. QU’EST-CE QU’UNE COMMUNAUTÉ ?

Une communauté se définit par rapport à un graphe courant comme un groupe de nœuds qui sont particulièrement reliés entre eux et faiblement reliés au reste du réseau. Il peut s’agir par exemple d’individus qui échangent beaucoup entre eux et peu avec les autres. Il est particulièrement intéressant d’identifier ces groupes afin de faire émerger la structure sous-jacente du graphe. On peut ainsi le diviser en groupes naturels d’individus (sans chevauchement, i.e. un nœud appartient à un unique groupe) qui peuvent être de toute taille. Cette identification va prendre en compte uniquement la structure du graphe, ainsi que les éventuels poids d’arêtes qui apportent de l’information supplémentaire, par exemple le niveau d’activité d’une relation.

2.  QUELS ALGORITHMES DE DÉTECTION ?

L’approche traditionnelle est de minimiser le taux de coupe (i.e le nombre d’arêtes inter-communautés) en réalisant un partitionnement, avec comme inconvénient principal de devoir choisir en amont le nombre de communautés.

Par la suite, une approche alternative visant à trouver des sous-groupes densément connectés s’est répandue, avec comme avantage de pouvoir sélectionner automatiquement le nombre de groupes. Elle comprend notamment les approches de maximisation de modularité, définie ci-dessous.

L’ensemble de ces approches sont non supervisées, on n’apprend pas à partir de communautés déjà labellisées.

Partitionnement par coupe d’arêtes

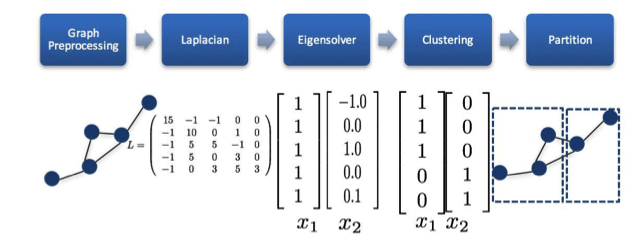
Clustering spectral : on souhaite partitionner en se basant sur un critère de coupe, i.e en coupant les arêtes ayant un poids faible, avec un choix ex-ante du nombre de communautés.

Etape 1 : On calcule la matrice Laplacienne, qui se définit telle que : L = D − A où D est la matrice des degrés, et Ala matrice d’adjacence. Il convient de la normaliser en cas de forte hétérogénéité des degrés.

Etape 2 : On calcule alors les k vecteurs propres de L correspondant aux k plus petites valeurs propres.

Etape 3 : On effectue un k-means sur la matrice contenant en colonnes les k vecteurs propres.

Girvan Newman (2008) utilise la edge-betweenness pour déduire des groupes. C’est le corollaire de la betweenness de nœud (ou intermédiarité), qui est une mesure de centralité : sur combien de plus courts chemins mon nœud est-il positionné ?

Girvan Newman étend cette notion aux arêtes. Cet algorithme offre des résultats de qualité et un raisonnement intuitif.

Etape 1 : On calcule la edge-betweenness de l’ensemble des arêtes

Etape 2 : Les arêtes avec la plus forte edge-betweeness, i.e qui ont le plus de chances d’être des ponts entre communautés, sont supprimées.

Etape 3 : Ces deux étapes sont répétées.

Le principal inconvénient est une forte complexité algorithmique, ce qui limite son usage à de petits graphes.

Identification de sous-groupes denses

La modularité Q est un score ∈ [−1; 1] (Newman 2006) qui compare, pour un groupe de nœuds, le nombre d’arêtes réel par rapport au nombre d’arêtes espéré (dans un réseau équivalent où les arêtes sont placées de façon aléatoire). S’il y a plus d’arêtes qu’espéré, alors on pourrait avoir un groupe. On obtient ainsi un score de division d’un réseau en modules (nos communautés).

Il est donc fréquent d’utiliser sa maximisation pour identifier des structures communautaires. Cependant, le problème exact de maximisation est NP complet, et par conséquent peu applicable sur des graphes de taille significative. Une version approximée a été publiée en 2004 par Clauset et al. : Fastgreedy (2004). Il fusionne de façon itérative les nœuds puis les groupes de nœuds ensemble de façon à optimiser la modularité globale de la structure communautaire, et crée ainsi un dendrogramme, qui est ”coupé” là où la modularité est maximale. Sur un graphe à n nœuds et m arêtes, sa complexité est de O(mdlogd) où d est la profondeur du dendrogramme qui décrit la structure communautaire.

Cependant, un problème a été identifié : la limite de résolution. Optimiser la modularité globale ne permets pas toujours d’identifier la structure communautaire d’un graphe sous l’hypothèse (souvent vérifiée) que la taille des groupes est très hétérogène. Fastgreedy a alors tendance à agréger des petits groupes d’individus en une super-communauté avec une faible cohérence interne. Cela pose deux problèmes : trouver les bonnes communautés, et le temps de calcul ralenti par ces agrégations superflues (compliqué pour plus d’un million de nœuds).

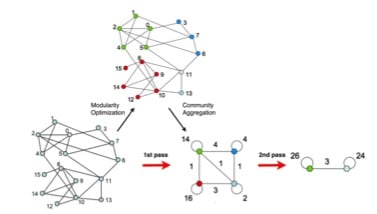
Des méthodes de résolution à multiples niveaux ont par conséquent été développées, et en particulier l’algorithme de Louvain, publié en 2008 par Blondel et al. Ici, on maximise la modularité locale, c’est à dire la modularité du groupe, et non pas de la structure communautaire.

Etape 1 : Chaque nœud est sa propre communauté. Pour chaque nœud, on cherche là où il augmente le plus la modularité du groupe, s’il existe un gain positif. On s’arrête lorsqu’il n’y a plus de gain possible. Un maximum local est alors atteint.

Etape 2 : on réitère en considérant une communauté comme un nœud. On stoppe lorsqu’il n’y a plus de gain positif issus de la fusion des communautés.

Ces deux étapes sont réitérées, en général 2-3 fois maximum, et on obtient un partitionnement final avec des communautés de tailles potentiellement très hétérogènes.

Louvain est un algorithme que l’on peut raisonnablement conseiller d’utiliser en première intention, en particulier sur des graphes de grande taille (plusieurs millions de nœuds, dizaines ou centaines de millions d’arêtes).

D’autres algorithmes existent et peuvent être tout aussi efficaces que les méthodes présentées précédemment. L’algorithme Walktrap (Pons, Latapy 2005), utilise une mesure de similarité entre nœuds basée sur des marches aléatoires. L’intuition est la suivante : une marche aléatoire a tendance à rester piégée au sein des communautés d’un graphe. Ainsi, elle est révélatrice de la structure du graphe et peut être utilisée pour comparer des nœuds : si le chemin de la marche aléatoire partant d’un nœud i est similaire à celui d’un nœud j, alors les deux nœuds ont une probabilité significative d’appartenir à la même communauté. On peut alors agréger de façon itérative comme pour l’algorithme Fastgreedy, et couper le dendrogramme là où la modularité est maximale.

Infomap (Rosvall et Bergstrom, 2008) et Label Propagation (Raghavan et al., 2007) sont également deux alternatives à considérer. Cependant, leurs performances n’étaient pas supérieures à d’autres algorithmes tels que Walktrap –dans les tests que j’ai pu réaliser- tout en étant moins intuitifs.

Attribution de multiples communautés à un nœud

Un algorithme attribue chaque nœud du graphe G à une unique communauté. Or, dans la vraie vie, un nœud peut, et va, appartenir à plusieurs groupes. Une solution de contournement peut être de passer au line graph L(G), où chaque nœud de L(G) est une arête de G et deux nœuds de L(G) sont connectés si et seulement si les deux arêtes qu’ils représentent ont un nœud commun. Par exemple, un graphe de trois nœuds, Alberto, Ysé et Adèle, avec une relation Alberto-Adèle et Ysé-Adèle, sera transformé en un line graph à deux nœud (Alberto-Adèle, Ysé-Adèle), qui auront une arête, car Adèle est une connaissance commune.

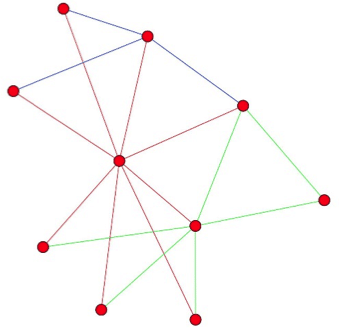
Appliquer les algorithmes de détection de communautés sur L(G) permet donc d’attribuer plusieurs communautés à un nœud, une fois revenus dans l’espace de G. On aura par conséquent un ”clustering d’arêtes” de G. Ici on voit un graphe généré, avec une application de ce clustering d’arêtes. On peut observer que plusieurs nœuds ont des arêtes de communautés différentes.

Quels algorithmes choisir ?

En première intention, pour les approches de maximisation de modularité, il convient de préférer Louvain à Fastgreedy, en raison de la limite de résolution et d’une scalabilité bien meilleure (plusieurs millions de nœuds et centaines de millions d’arêtes en 13 minutes sur une Qbox par exemple). Louvain fait d’ailleurs partie des algorithmes de détection de communauté les plus rapides (plus que Walktrap par exemple).

Quels outils ?

Plusieurs outils peuvent être envisagés :

Gephi est un outil packagé, NetworkX une librairie pur Python, graph-tool est en C++ avec un wrapper Python, Igraph est en C avec un wrapper R et Python. De nombreux comparatifs formels peuvent être trouvés sur les fonctionnalités détaillées et les performances.

En quelques mots, je dirais que Gephi a l’avantage de la facilité et ne nécessite pas de compétences en programmation. Si on est prêt à coder un minimum, NetworkX peut être un bon début car il possède de nombreuses fonctionnalités, mais offre les performances très limitées de Python. Igraph et graph-tool sont bien plus performants, avec de nombreuses fonctionnalités également, et sont facile d’accès. Personnellement, je recommanderais Igraph, qui est particulièrement riche en algorithmes de détection de communautés déjà packagés.

Ainsi, le code suivant permet d’appliquer Walktrap à mon objet graph -qui retourne un dendrogramme-, choisir le nombre de clusters là où la modularité est maximale (mais on peut choisir le nombre que l’on souhaite), ajouter le cluster d’appartenance en attribut de nœud, et représenter le graphique avec les communautés en couleur.

On obtient alors les communautés du réseau (en l’occurence parmi mes contacts LinkedIn), et peut analyser ces communautés : sont-elles caractérisées par des métiers, des lieux communs, ont-elles des densités particulièrement élevées etc. On peut alors analyser la structure communautaire et interpréter ces sous-groupes.

Remarque : On peut constater que certains nœuds sont à cheval entre plusieurs communautés (ex : le nœud du milieu est entre la communauté jaune et verte). En passant au line graph, ces nœuds apparaitront comme des ponts entre deux clusters d’arêtes.

Sur de petites graphes (<500 nœuds maximum), Girvan Newman offre des résultats de qualité, avec par ailleurs une intuition facilement compréhensible. Sa complexité algorithmique l’empêche cependant d’être utilisé sur des volumétries plus importantes.

Walktrap peut être une bonne deuxième approche, non basée sur la modularité. Il est cependant plus lent que Louvain et peut avoir des difficultés à différencier des groupes en cas de composante fortement connectée.

GraphX est la librairie Spark d’analyses de graphes. Mis à part son intérêt intrinsèque lié à la scalabilité, le jeu de fonctionnalités est forcément plus limité, de nombreux algorithmes n’étant pas parallélisables et complexes par nature. On peut cependant y trouver le Pagerank, compter les triangles du graphe, et des algorithmes de coupe visant à partitionner le graphe.

Pour finir, certains algorithmes sont embarqués dans des bases orientées graphe, comme Louvain et Label Propagation sur Neo4J.

Quels jeux de données ?

Plusieurs formats standards de données graphes existent (graphML etc), mais in fine on doit avoir une liste de nœuds, ainsi qu’une liste d’arêtes. On ne peut que recommander le site SNAP, i.e la Stanford Large Network Dataset Collection, qui contient des jeux de données libres de type réseaux sociaux (Twitter par exemple), produits (Amazon), de communautés en ligne (Reddit) etc. Il y a en particulier des jeux de données comportant des communautés labellisées qui peuvent être un parfait outil pour tester ces types d’algorithmes. Par ailleurs, Twitterdispose d’une API assez ouverte qui permet relativement aisément de récupérer son réseau, ce qui n’est malheureusement plus le cas de LinkedIn.

4. MÉTRIQUES DE PERFORMANCE

Une grande question de la détection de communautés est : ont-elles du sens ? Sont-elles correctes ?

Cette question est loin d’être triviale, car lorsqu’on y réfléchit, il est difficile de fixer un nombre limité et exact de groupes parmi ses amis. On peut partitionner de multiples façons, et on n’aura pas le même nombre et les mêmes appartenances en fonction de la granularité choisie.

Formellement, on peut différencier deux cas : les ”vraies” communautés sont connues (avec toute la relativité que cette notion implique) ou pas.

Données labellisées

Lorsque les vraies communautés sont connues, les métriques de performance sont assez aisément identifiables, on veut comparer la partition prédite à la partition réelle, ce qui revient à comparer des listes. Les métriques standard de comparaison de clusters sont alors applicables. On peut par exemple utiliser la Normalized Mutual Information (Dannon et Al 2005), qui est un score standard compris entre 0 et 1, ou l’indice de Rand (Rand, 1971).

Données non labellisées

En cas de données non labellisées, ce qui est bien sûr le cas le plus fréquent, cette question est plus complexe.

On peut avoir deux approches :

— Interpréter avec toute l’information disponible la structure communautaire afin de conclure sur leur signification. Dans le cas LinkedIn, on a le poste des personnes, leur entreprise actuelle, des lieux. On peut alors, sans connaissance a priori, voir si un lieu est surreprésenté, ou un poste etc. On croisera ces informations avec l’information connue au départ. On peut également entraîner un arbre de décision sur les clusters pour identifier de façon automatisée les caractéristiques les plus utiles.

— Analyser la structure : la modularité de la structure communautaire obtenue est une première indication. Si elle est inférieure à 0.3, elle est peu satisfaisante, et plus elle est proche de 1, mieux c’est. Sur l’exemple LinkedIn, elle est de 0.44. On peut également vérifier la densité des principaux groupes obtenus. Dans le réseau LinkedIn global, elle est de 7 %, alors que dans la communauté verte elle est de 32%, et jusqu’à 65% dans une sous-structure de cette communauté. On a alors les deux tiers des liens possibles qui existent, et il y a donc bien un sous-groupe fortement connecté. On peut également définir une métrique custom basée sur le niveau de connectivité au sein des communautés par rapport au graphe global, ou du taux de coupe nécessaire pour les isoler complètement.

5. CAS D’APPLICATION ET CONCLUSION

Ce type d’approches peut être appliqué à plusieurs cas d’usages et sur plusieurs types d’entités :

— Marketing digital : Identifier la structure d’un réseau peut permettre d’optimiser la diffusion d’un message ou d’une marque, en complémentarité de l’analyse des centralités, i.e l’influence d’un nœud, qui sera détaillée dans le prochain article de cette série sur les graphes. Plutôt que de sponsoriser deux bloggeurs qui ont potentiellement un grand nombre d’abonnés en commun, on peut avoir tout intérêt à identifier deux individus qui font partie de groupes disjoints. Dans un autre registre, identifier des communautés de produits peut permettre d’améliorer un moteur de recommandation, afin d’identifier des produits possibles en cross-selling.

— Détection de fraude et analyse de liens : L’analyse de réseaux est étudiée de longue date dans le cadre d’investigations (fraude, liens financiers, terrorisme…). En effet, un nombre significatif d’actions sont menées en ”bande organisée”. Les algorithmes et outils cités précédemment peuvent permettre de faciliter ce type d’analyses, et ont notamment été utilisées dans le cas des Panama Papers afin d’extraire de l’information de la multitude de documents et liens, ainsi que pour Anacrim afin d’identifier des suspects.

— RH analytics : Dans le cadre d’un grand groupe, le téléchargement de logiciels via une plateforme centrale peut permettre d’identifier des communautés de compétences, et ainsi, mieux orienter sa politique de formation et de mobilité interne.

Cette liste n’est pas exhaustive, et les champs d’applications sont vastes. De nombreux challenges restent dans ce domaine, et en particulier la prise en compte de la dynamique d’une structure communautaire. Des groupes se créent, évoluent et disparaissent dans le temps, et cette dimension est encore difficile à prendre en compte.

Dans le prochain article de notre série sur la théorie des graphes, l’analyse de centralités, i.e le type d’influence d’un individu, un autre champ passionnant de la théorie des graphes sera expliqué.

RÉFÉRENCES

— M. E. J. Newman, Modularity and community structure in networks , Proc. Natl. Acad. Sci. USA, vol 103 no 23 2006, p. 8577–8582

— Aaron Clauset,1 M. E. J. Newman,2 and Cristopher Moore1, 2004, ”Finding community structure in very large networks”, arXiv :cond-mat/0408187

— Vincent D. Blondel, Jean-Loup Guillaume, Lambiotte1„ and Etienne Lefebvre, 2008, ”Fast unfolding of communities in large networks” arXiv :0803.0476v2 [physics.soc-ph]

— Danon L, Diaz-Guilera A, Duch J, Arenas A : Comparing community structure identification. J Stat Mech P09008, 2005.

— Pascal Pons and Matthieu Latapy, 2005, Computing communities in large networks using random walks, arXiv :physics/0512106 [physics.soc-ph]

— Raghavan, Albert and Kumara (2007), Near linear time algorithm to detect community structures in large-scale networks, Physical Review E 76, 036106, arXiv :0709.2938

— Rand WM : Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 66(336) :846-850, 1971.

— Rosvall M, Bergstrom CT (2008) Maps of random walks on complex networks reveal community structure. Proc Natl Acad Sci USA 105 :111