Tout est graphe ! Introduction à une théorie aux applications multiformes

Réseaux sociaux, réseaux de transport, réseau électrique, réseaux de neurones, réseau alimentaire …. On peine à trouver des systèmes plus hétérogènes entre eux, et néanmoins ils partagent une partie de leur nom : ils sont tous des « réseaux ». Mais alors c’est quoi cette idée qui nous permet de décrire des entités si différentes, quelle est son origine, quels sont les problèmes que nous pouvons résoudre grâce à cette approche ? Suivez-nous dans cette série d’articles sur la théorie des graphes pour trouver les réponses !

A l’origine des graphes, des ponts et des lignes de métro

C’est rare de connaître avec exactitude l’origine d’une branche mathématique, mais c’est bien le cas ici. C’est pour ça que notre voyage dans la théorie des graphes commence dans la ville de Königsberg, construite autour de deux îles reliées par un pont (voir fig. 1). Six autres ponts existaient pour relier les deux rives à l’une ou à l’autre des deux îles. Au XVII siècle, les habitants commencèrent à se demander s’il était possible de se promener dans la ville en traversant chaque pont une et une seule fois, pour revenir in fine au point de départ.

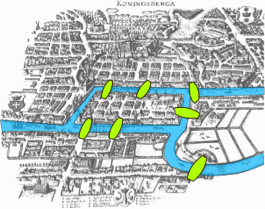
Fig. 1 : La ville de Königsberg, avec ses deux îles, et ses sept ponts

Cette question serait sans doute très vite tombée dans l’oubli, si ce n’était pas pour un mathématicien suisse, Leonard Euler, qui trouva la solution avec une méthode remarquable. Il comprit que dans la description du problème il y avait beaucoup d’informations inutiles : la dimension des îles, la position précise des ponts, leur longueur …. Trouver une manière de représenter seulement les informations vraiment nécessaires lui aurait permis de trouver plus aisément la solution. Mais qu’est-ce qu’il lui fallait, du coup, pour savoir si la balade tant désirée par les habitants de Königsberg était possible ou pas ? Au final, pas grand-chose : juste quelles étaient les zones de la ville (quatre : les deux îles plus les deux rives) et, pour chaque pont, quelles étaient les deux zones qu’il reliait. Une fois le schéma présenté en fig. 2 obtenu, la solution fut presque évidente : la promenade demandée n’était pas possible à cause des zones touchées par un nombre impair de ponts. Au fait, il faut toujours arriver dans une zone par un pont et en repartir en utilisant un autre : le nombre impair nous empêche de le faire.

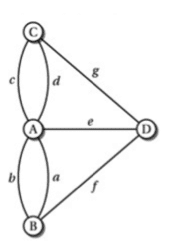
Fig. 2 : Les informations nécessaires pour résoudre le problème

Beaucoup plus intéressant que la solution, en tout cas, est la démarche utilisée ici pour la première fois : prendre un système très compliqué, et en représenter juste sa structure de graphe, c’est-à-dire ses éléments (dans l’exemple, les quatre zones) et les connexions existantes entre eux (dans l’exemple, les sept ponts). La théorie des graphes était officiellement née !

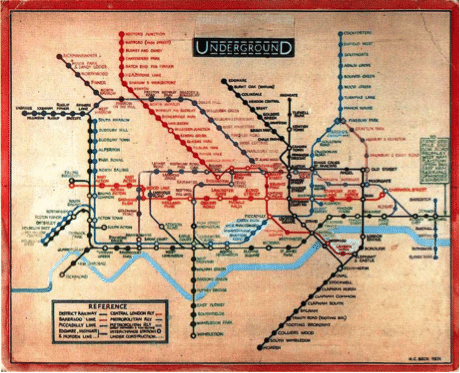
Comme toutes les choses intéressantes, les graphes aussi ont été inventés plusieurs fois. Jusqu’au début des années ’30, la carte des transports de Londres représentait la ville de manière très naturelle : lacs, fleuves, champs cultivés (voir fig. 3) … De plus, les lignes aussi étaient représentées de manière réaliste, avec leurs courbatures et leurs croisements bizarres. Le développement des lignes dans les banlieues rendait très difficile une vision complète de la partie la plus intéressante de la carte, le centre-ville étant comprimé dans une petite fraction de la carte.

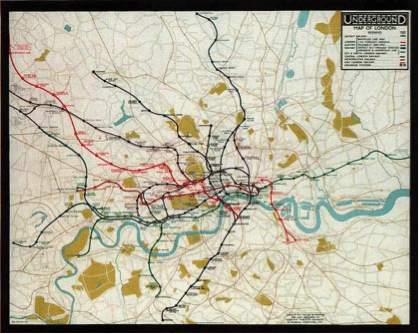
Fig . 3 : La carte des métros de Londres utilisées jusqu’aux années 1920

●      Pas de contexte sur la ville « en surface » si on exclut la présence du Tamise

●      Échelle variable (plus large dans le centre-ville pour zoomer sur la partie la plus utilisée et difficile à lire)

●      Parcours des lignes représentées de manière abstraite, avec des droites horizontales, verticales ou à 45 degrés.

Vrais graphes, graphes approximés

Dans les deux exemples précédents, la description en tant que graphe nous permet de garder toute l’information intéressante d’un système. Dans d’autres cas, une démarche similaire nous permet de définir des systèmes simplifiés, qui ont perdu une partie de leur richesse. Si nous pensons au cerveau humain, énormément de facteurs en déterminent le fonctionnement : mais comme la compréhension complète d’un système d’une telle complexité est pour l’instant du domaine de la science-fiction, des aperçus peuvent être obtenus en l’analysant en tant que graphe, c’est-à-dire en prenant en compte juste les neurones (les nœuds du graphe) et les synapses (les interconnexions). Il en va de même pour d’autres cas d’usage, tels que l’économie, les écosystèmes, la logistique, les réseaux sociaux.

Comme le statisticien George Box le disait, tous les modèles sont faux ; mais certains sont utiles : rien nous empêche par exemple de modéliser les échanges économiques comme un graphe pour en identifier la structure, et d’utiliser d’autres modélisations pour en comprendre d’autres aspects. C’est à nous de choisir, et la théorie des graphes est au final un outil que nous pouvons décider d’utiliser ou pas en fonction du contexte.

Le passage entre le système d’origine et sa version graphe n’est pas univoque : dans les échanges économiques, un nœud pourrait aussi bien représenter un pays, ou une personne, ou une entité juridique, ou encore un ménage. Pas de règles prédéfinies qui nous disent quand et comment passer à un graphe : la modélisation la plus pertinente s’apprend sur le terrain, après beaucoup d’essais qui nous mènent vers des impasses ….

Comment représenter et caractériser un graphe ?

Un graphe est d’habitude représenté d’une manière visuelle, avec ses nœuds affichés comme des points, et ses liens qui sont des flèches, ou des traits entre les points (voir fig. 2). Ce schéma, très utile pour se faire une idée préliminaire du système, n’est pas très adapté pour faire des calculs ; si nous étudions un système avec des millions de nœuds, nous sommes aussi forcés à en afficher à chaque fois une partie très limitée.

Une approche complémentaire, et beaucoup plus utilisée en pratique, est de représenter le graphe avec sa matrice d’adjacence, dans laquelle la valeur en position (i,j) est 1 si un lien existe entre le nœud i et le nœud j, et 0 autrement. Le même principe peut être adopté pour des graphes pondérés (où les liens peuvent être plus ou moins fortes), et pour des graphes directionnels (dans lesquels si A est connecté à B, nous ne savons pas si B est connecté avec A aussi : pensons aux célébrités sur Twitter, qui ont beaucoup de followers sans pour autant tous les suivre).

Pour ce qui concerne la caractérisation quantitative d’un graphe, nous pouvons utiliser des métriques locales (valables à proximité d’un nœud) ou globales. Parmi les métriques locales, nous trouvons le degré d’un nœud : combien d’arêtes convergent vers lui. Parmi les globales, on peut au moins rappeler :

● Le coefficient de clustering, qui dans un graphe social consiste à se demander avec quelle probabilité deux personnes que je connais se connaissent entre elles. En général, nous voulons déterminer combien parmi les couples de nœuds avec un voisin en commun sont connectés. Dans un graphe réel, ce coefficient est d’habitude très élevé : deux parmi mes amis ont beaucoup plus de chances de se connaître que deux personnes choisies aléatoirement ;

● La distance moyenne entre deux points, i.e. combien de marches sur le graphe je dois faire, en moyenne, pour me déplacer d’un point A à un point B en utilisant exclusivement les arêtes du graphe. Cette distance est souvent petite pour les graphes réels, ce qui a donnée origine à la célèbre « théorie » des six degrés de séparations entre nous et n’importe quelle autre personne sur la planète. Au fait, le nombre six est spécifique à une expérience conduite dans les années ‘60 par Stanley Milgram, et dans les réseaux sociaux actuels ce chiffre est encore plus petit. La distance maximale entre un couple de point est appelée le diamètre du graphe ;

● La densité du graphe, c’est-à-dire combien parmi les liens possibles existent. Le nombre maximal d’arêtes pour un graphe de N nœuds est N*(N-1)/2 et correspond au cas dans lequel chaque nœud est connecté avec tous les autres. En général, la densité d’un graphe est beaucoup plus faible, et chaque élément a un nombre de connexions qui change très peu pour un changement de N : que Facebook ait 500 millions ou 2 milliards d’utilisateurs, le nombre de mes amis changera de manière très marginale. On parle alors de graphe creux.

Quels problèmes peuvent être abordés grâce à la théorie de graphes ?

C’est bien de savoir que, par exemple, les interactions économiques peuvent être représentées comme un graphe. Mais une fois que nous avons fait ça, quelles sont les questions auxquelles nous pouvons chercher une réponse ?

Dans les prochains volets de cette série, nous rentrerons plus dans le détail de certains parmi ces cas d’applications ; pour l’instant, voici les grandes catégories de problèmes qu’on peut définir sur les graphes.

Analyse de la robustesse

Théorie qui s’occupe de comprendre l’effet d’une modification du réseau existant. L’objectif peut être de vérifier si le système continuera à marcher correctement après un changement prévu, ou bien de tester sa résilience à une défaillance aléatoire, ou encore à une attaque ciblée. Dans un autre contexte, comprendre l’effet de la disparition d’une certain espèce animale menacée dans un écosystème rentre dans la même logique. Le résultat d’une telle analyse permet de déterminer quels sont les éléments à protéger avec une attention particulière car cruciaux pour le fonctionnement global du système.

Fig. 5 : L’analyse de la robustesse de ce système risque de ne pas donner des résultats très satisfaisants …

Quels sont les nœuds et les arêtes les plus importants dans un graphe ? Cette question, qui peut trouver beaucoup de réponses différentes (pensons à un graphe social : qu’est-ce qu’une personne « importante » ? Pas de réponse univoque !) peut aussi être adressée de manière structurelle, en regardant juste qui est connecté avec qui. On peut penser qu’un élément est important s’il est connecté avec beaucoup d’autres éléments importants : cette idée très logique a donné origine, il y a une quinzaine d’année, à un algorithme qui a plutôt bien marché : il s’agit de PageRank, utilisé par Google pour proposer des réponses pertinentes à nos requêtes ….

Détection de communautés

La structure d’un graphe réel est loin d’être aléatoire. En particulier, nous y trouvons typiquement des sous-parties qui sont beaucoup plus connectées internement qu’avec ce qu’il y a à l’extérieur. On peut ici penser à un groupe d’amis : la probabilité pour chacun d’entre eux d’être lié à un membre du groupe est énormément plus élevée que celle d’être lié à une autre personne arbitraire.

Un sujet à part entière de la théorie des graphes consiste à définir de manière claire et à chercher dans un graphe cette structure communautaire. Ce cas d’usage, sur lequel nous avons pu travailler beaucoup, fera l’objet d’un des prochains articles de cette série.

Fig. 6 : Un graphe qui présente une structure en communautés

Comprendre la dynamique des propagations sur un réseau peut être d’extrême importance. D’un côté, nous pouvons chercher de bloquer la diffusion d’un virus informatique, ou d’une épidémie, le plus rapidement possible. Dans d’autres situations, le but peut être au contraire d’augmenter au maximum la vitesse de propagation d’une information. Paradoxalement, la mathématique derrière ces deux cas d’usage est très similaire, et consiste à chercher les meilleurs épandeurs dans le système. Dans le premier cas, ce seront les éléments à protéger, ou à vacciner ; dans le deuxième, on les utilisera comme cible de notre campagne de marketing viral. En suivant le même principe, nous pouvons aussi estimer les possibles effets de boules de neige dans les défaillances d’un système, pour prévoir si les dégâts resteront localisés ou si un risque d’endommagement global existe.

Rendez-vous au prochain épisode de la série pour aller encore plus loin dans les idées applicables aux systèmes qui ont une structure de graphe …. c’est-à-dire à n’importe quel système !