Comment choisir sa fonction de perte en Computer Vision ? - Partie 2

Cet article fait suite au précédent article sur Comment choisir sa fonction de perte en Computer Vision ? – Partie 1. Dans celui-ci, nous abordons les deux derniers cas d’usage, à savoir la segmentation sémantique et la segmentation d’instance, toujours avec notre animal favori : le chat 😽

Cas d’usage n°3 : segmenter les chats sur l’image (segmentation sémantique)

Présentation du cas d’usage

Le cas d’usage de la segmentation sémantique présente de nombreuses similarités avec le premier cas d’usage sur la classification d’image. Dans les faits, au lieu de classifier une image entière, ici nous classifions chaque pixel de l’image. Pour une segmentation binaire, comme ici, la classe opposée à la classe cible est souvent appelée « autre » ou « background » en anglais, puisqu’il s’agit de tout ce qui se trouve « en fond » de l’objet segmenté.À la différence d’une classification d’image, le nombre de prédictions est totalement différent dans ce troisième cas d’usage. En effet, puisque nous allons classifier des pixels et non des images, le nombre de prédictions sera démultiplié en fonction de la taille des images.

Choisir sa fonction

Entropie croisée binaire pondérée (Weighted Binary Cross-Entropy)

En temps normal, la binary cross-entropy suffit largement à effectuer le travail désiré. Cependant, rappelons-nous que nous sommes dans une classification binaire. Ce qui revient à se dire : « Est-ce que le pixel appartient à ma classe cible ? Oui ou non. ». De ce fait, il risque d’y avoir beaucoup plus de pixels appartenant à la classe background qu’à notre classe cible, créant alors un déséquilibre entre les deux classes. C’est ici que nous introduisons la weigthed binary cross-entropy afin de compenser le déséquilibre entre les deux classes. Elle attribue ainsi un poids plus lourd β aux erreurs faites dans notre classe cible, afin de compenser le faible nombre de prédictions dans celle-ci et ne pas laisser le modèle sur-apprendre la classe background.

Focal loss

La focal loss se présente comme une version améliorée de la BCE (Binary Cross Entropy). Elle lui attribue un poids qui tend vers zéro à mesure que la confiance dans la classe cible augmente, permettant de rééchelonner le résultat de façon dynamique. À contrario de la WBCE (Weighted Binary Cross Entropy), ce facteur est fait pour donner moins d’importance aux exemples dits « simples » et permet de se focaliser sur les exemples plus compliqués. Ce facteur est composé de la probabilité ressortie par le modèle  , ainsi que d’un hyperparamètre 𝛾 :

Mis bout à bout avec la formule de la BCE, on a :

En choisissant un  𝛾 > 0, l’importance donnée aux exemples « simples » est réduite, et inversement. En général, une valeur de 2 pour 𝛾 fonctionne correctement.

Indice de Jaccard (ou Intersection Over Union)

L’indice de Jaccard est une mesure utilisée pour comparer la similarité entre deux ensembles. Dans notre cas, les deux ensembles correspondent à l’objet à prédire, et son label. Cette mesure, plus souvent appelée IoU en Computer Vision, vise à donner plus d’importance aux prédictions correctement placées et à pénaliser les prédictions décalées par rapport à leur label. De cette façon, la précision des prédictions du modèle est améliorée.

Avec TP, FP et FN représentant respectivement le nombre de pixels en True Positive, False Positive et False Negative.

Coefficient de Dice (ou Dice loss ou F1-Score)

Le coefficient de Dice ou encore F1-Score, est une variante de l’IoU présentée précédemment. Les deux fonctions sont corrélées positivement, par conséquent, si un modèle A possède un meilleur score qu’un modèle B selon l’une des deux fonctions, alors il en sera de même pour l’autre fonction. La différence entre les deux fonctions se fera ressentir lorsqu’il y aura généralisation à tout le jeu de données. Au même titre que la MSE (Mean Squared Error) et la MAE (Mean Absolute Error), là où l’IoU (MSE) aura tendance à pénaliser les grosses erreurs, le coefficient de Dice (MAE) aura plutôt tendance à lisser la perte pour en être le moins affecté.

Dans le cas multi-classes/multi-labels

En segmentation, le multi-classes induit très souvent le multi-labels car il est rare de ne pas avoir les différentes classes mixées dans une même image. Ici, le multi-labels réfère au cas d’une image qui contient des pixels pouvant provenir de plus de deux classes différentes (background exclu).

Pour un cas multi-classes, et donc multi-labels, la weighted binary cross-entropy sera encore une fois votre alliée. Néanmoins, il reste possible d’utiliser les autres fonctions telles que Dice ou l’IoU, en l’appliquant à chacune des classes de l’image prédite, puis en faisant la moyenne (éventuellement pondérée) sur toutes les classes pour obtenir un score final sur l’image. C’est souvent le cas avec l’IoU, qu’on retrouve alors sous le nom mIoU pour Mean Intersect Over Union.

Pourquoi ?

En segmentation, il est souvent important que le masque prédit soit suffisamment précis et ne déborde pas trop de sa cible. Pour évaluer cela, les fonctions de perte IoU et Dice sont les plus adaptées car elles prennent en compte la forme de la prédiction. En revanche, le choix entre les deux sera fait par le Data Scientist, en fonction de s’il désire pénaliser plus fortement son modèle lorsqu’il fournit de mauvaises prédictions à une échelle locale ou s’il préfère avoir une pénalisation plus globale sur les erreurs du modèle.

Le choix de l’une ou de l’autre à la place d’une focal loss ou d’une cross-entropy peut se justifier par le fait qu’il n’est pas nécessaire d’avoir recours à un hyperparamètre pour l’optimisation du modèle. L’introduction de poids dans la weighted cross-entropy ou du β dans la focal loss rend la paramétrisation de la fonction de perte plus délicate. D’une manière générale, la Dice loss est l’une des fonctions de perte les plus utilisées pour une tâche de segmentation sémantique.

Cas d’usage n°4 : détecter et segmenter les chats sur l’image (segmentation d’instance)

Présentation du cas d’usage

Pour ce quatrième et dernier cas d’usage, nous élargissons le périmètre des précédents cas d’usage et choisissons de faire de la segmentation d’instance sur nos trois petits chats.Comme évoqué précédemment, la segmentation d’instance est en quelque sorte la fusion des trois précédentes méthodes. Quant au choix des fonctions de perte, aussi simple que cela puisse paraître, il sera sensiblement similaire à celui fait dans les autres cas.

Choisir sa fonction

La segmentation d’instance combine classification, régression et segmentation, il y a par conséquent 3 fonctions de perte différentes à appliquer. Au même titre que lorsque nous avions complexifié le cas d’usage 1 en rajoutant la localisation de l’objet pour faire de la détection d’objet, nous complexifions ici encore une fois la tâche en rajoutant l’instantiation à la segmentation. Puisqu’il s’agit des 3 cas d’usage que nous venons de voir, et pour éviter toute redondance, je vous invite à vous référer à ces derniers pour le choix des fonctions.

Pourquoi ?

Ici, il n’y a plus de nouveautés, et donc, plus de secrets pour vous ! Pour chacune des branches du modèles, les fonctions de perte disponibles seront les mêmes que celles des cas d’usage présentés précédemment. Cependant, nous avions mentionné que ce cas d’usage était le plus compliqué du fait de la structure des modèles utilisés. Cela se répercute en effet dans les critères de choix des fonctions de perte utilisées. Ces critères dépendront surtout de la structure du modèle ou de l’optimisation des calculs, plutôt que de la nature de la problématique en elle-même (mono-classe, multi-labels, etc…) où les choix respectifs seront finalement plus « triviaux ».

Conclusion

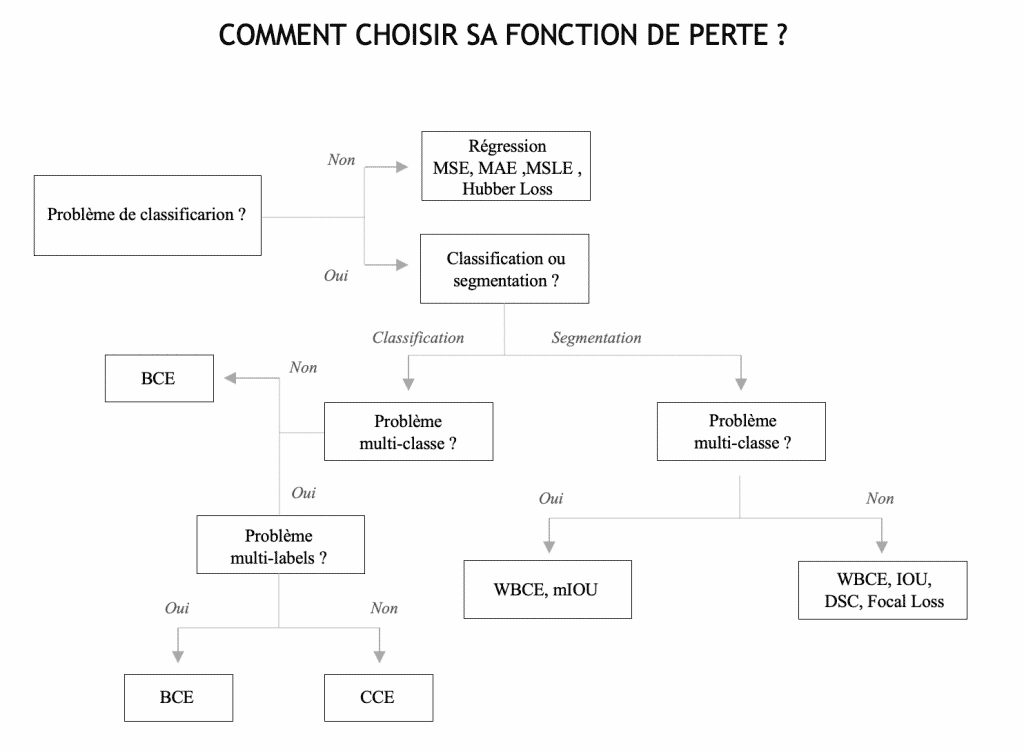
Vous avez désormais toutes les cartes en mains pour choisir une fonction de perte adaptée pour les cas d’usage les plus classiques de la computer vision. Comme mentionné au début de cette série d’article, toutes les fonctions existantes et tous les cas en computer vision n’ont pas été traités ici. Je traiterai des cas d’usage plus spécifiques et leurs fonctions de perte associées dans un prochain article. En attendant, je vous laisse avec ce diagramme récapitulatif qui, je l’espère, vous sera de bon usage 😉

Abonnez vous à notre page Quantmetry pour ne rien manquer de notre actualité ! 

Les membres de l’expertise Computer Vision adressent des thématiques couvrant l’ensemble du cycle de valorisation des images : de la constitution du jeu de données à l’implémentation du modèle sur des dispositifs embarqués.

Julian LE GOUIC

Data Scientist chez Quantmetry

Passionné par le Deep Learning, je me suis très vite spécialisé vers le domaine de la Computer Vision après un double diplôme en Data Science et Informatique & Systèmes intelligents. J’applique aujourd’hui mes compétences dans diverses missions de Computer Vision, mais pas seulement !