Corriger les biais algorithmiques en IA grâce à l’Adaptation de Domaine par Transport Optimal
Lorsque nous utilisons un modèle de Machine ou Deep Learning, nous considérons que les données du jeu d’entraînement sont comparables à celles sur lesquelles le modèle est appliqué, c’est-à-dire qu’elles suivent la même distribution de probabilité. Néanmoins il arrive que cette hypothèse soit fausse : soit parce que le contexte est différent, soit parce que les données dérivent au cours du temps.
Nous allons dans cet article étudier la faisabilité et la pertinence d’utiliser la méthode du Transport Optimal afin de corriger ces différences de distributions de probabilité à travers un cas d’usage, lié aux perturbations induites pas la pandémie de Covid-19, orienté Time Series.
Qu’est-ce que l’Adaptation de Domaine ?
En Computer vision, la figure 1 illustre cette différence entre les données d’entraînement et données réelles. La distribution des covariables (ici les images) change car les arrière-plans sont différents, mais l’article à identifier reste le même donc le lien entre covariables et labels est inchangé.
Nous parlons alors de dérive virtuelle des données (en anglais covariate shift).

Figure 1 : A gauche, données d’entraînement // à droite, données réelles
L’hypothèse se vérifie aussi en NLP. Prenons l’exemple de la reconnaissance vocale d’un téléphone lorsqu’il y a changement d’utilisateur : le signal d’entrée est différent mais la sortie attendue est la même.
Il existe d’autres types de dérives qui ne seront pas traités dans cet article, notamment la dérive réelle (en anglais prior shift) où le label associé à un individu donné évolue au cours du temps.
Dans tous les cas, ces dérives induisent des pertes de performance dans les modèles. L’adaptation de domaine est un ensemble de techniques permettant de mitiger les pertes de performances induites par les dérives virtuelles. Il s’agit d’une sous-catégorie du transfert learning, qui désigne l’ensemble des méthodes qui permettent de transférer les connaissances acquises à partir de la résolution de problèmes donnés pour traiter un autre problème.
Dans la suite, nous considérerons le cas où nous souhaitons entraîner un modèle sur un jeu de données source et l’utiliser sur un jeu de données cible qui a une distribution différente. Dans le cas de la Figure 1, il suffit simplement de détourer les articles du jeu de test afin de rendre l’arrière-plan blanc, comme c’est le cas pour le jeu d’entraînement. Dans le cas général, il n’existe cependant pas de transformation naturelle. L’intuition de l’adaptation de domaine par transport optimal est de calculer une transformation qui envoie les individus du jeu cible sur le jeu source afin de leur appliquer notre modèle.
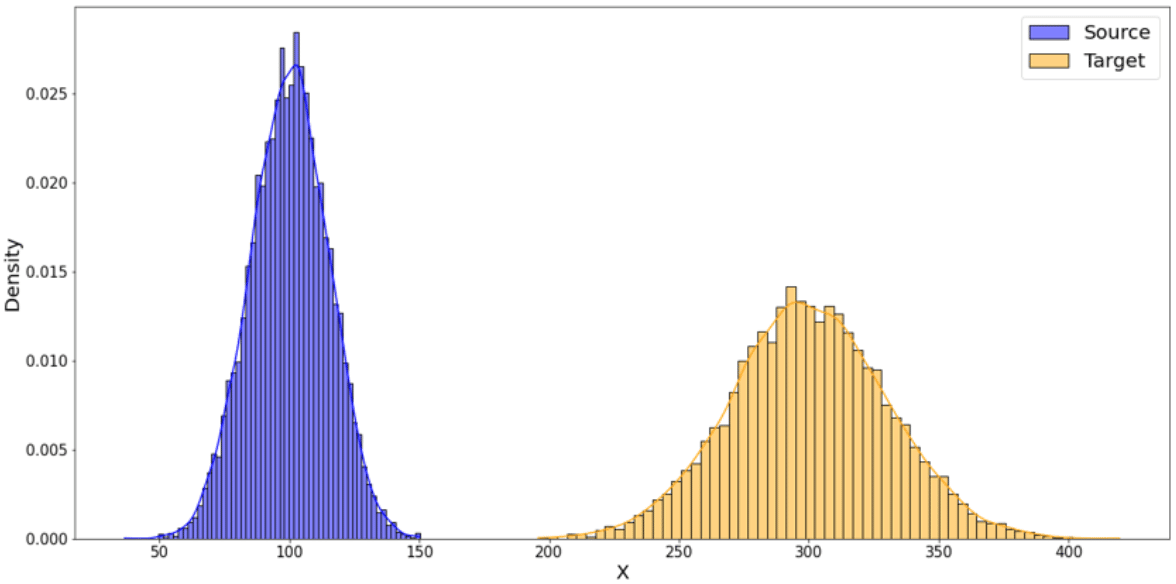
Figure 2 : en bleu, distribution source // en jaune, distribution cible
Qu’est-ce que le transport optimal ?
Gaspard Monge pose pour la première fois en 1781 la problématique du transport optimal lorsqu’il se demande comment transporter à moindre coûts des tas de sable vers des trous à boucher. Le coût à minimiser est la somme des distances parcourues, pondérées par la quantité de sable transportée. Ce n’est qu’en 1942 que Leonid Kantorovich viendra généraliser les formules élaborées par Monge.
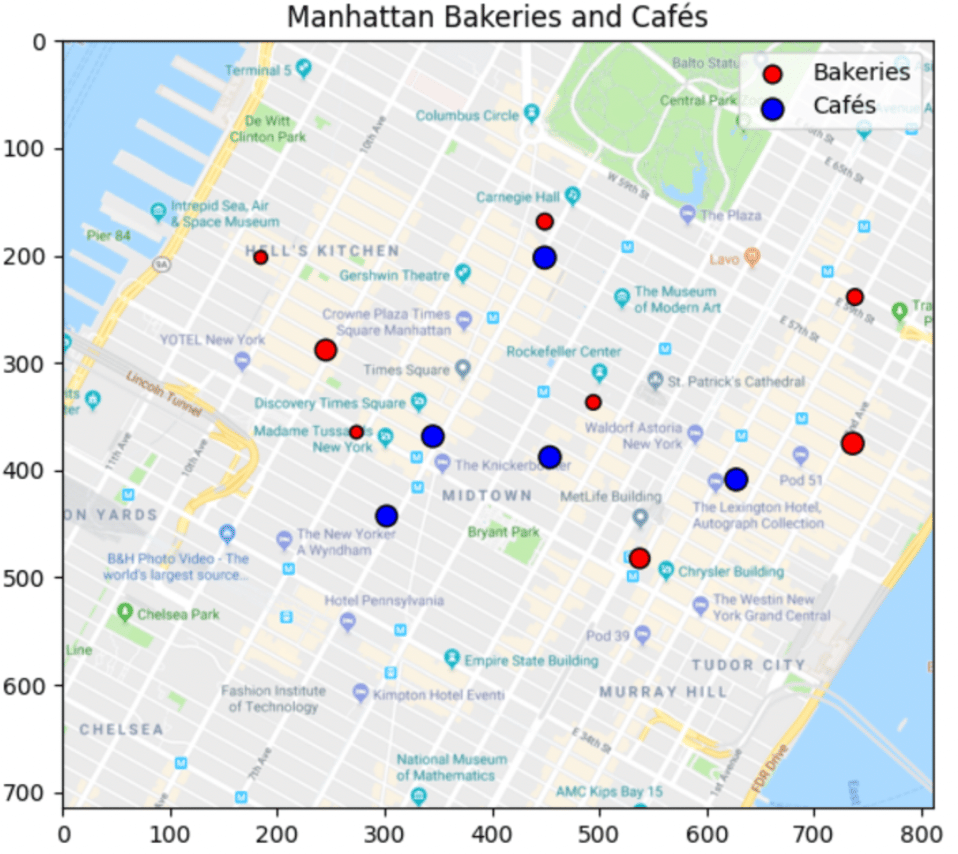
Figure 3 : emplacement des boulangeries et cafés
Imaginons le cas pratique où des croissants sont produits par plusieurs boulangeries et livrés à plusieurs cafés souhaitant les vendre. Nous supposons que les quantités totales produites par les premières et requises par les secondes sont fixées et égales. Comment organiser les livraisons de sorte à minimiser les coûts de transport ?
Si nous indexons les boulangeries par i et les cafés par j, nous pouvons noter :
- Cij la distance entre la boulangerie i et le café j
- a_i la quantité de croissants produite par la boulangerie i
- b_j la quantité de croissants requis par le café j
- P_ij la quantité inconnue de croissants à livrer de la boulangerie i vers le café j
Nous cherchons à trouver la matrice de couplage P qui permette de minimiser le coût sous contrainte de positivité de ses coefficients (nous transportons des quantités de croissants positives), d’écouler la production et de satisfaire la demande. En d’autres termes, nous cherchons combien de croissants chaque boulangerie doit envoyer à chaque café en prenant en compte les distances entre les boulangeries et les cafés.
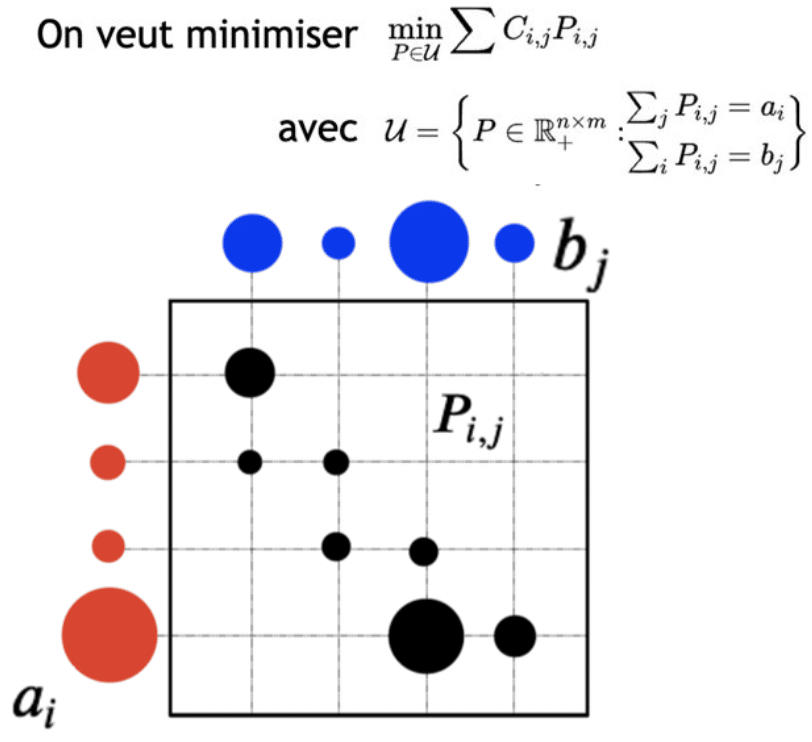
Figure 4 : illustration de la matrice de couplage à trouver
Le cas d’usage pour la mise en œuvre d’une solution via la théorie du Transport Optimal concerne le déplacement de données Source vers des données Cibles. Plus particulièrement, nous allons déplacer des distributions de probabilité issues de données temporelles : cas discret avec un nombre fini de sources et de cibles.
A présent, remplaçons les boulangeries par les individus de notre jeu de données source, et les cafés par les individus de notre jeu de données cible. Dans cette situation, nous ne cherchons pas à transporter la masse de nos distributions exactement, mais plutôt à créer une transformation régulière de la source vers la cible. Pour cela, nous résolvons une version relaxée du problème grâce à l’algorithme de Sinkhorn, ce qui permet de gagner significativement en temps de calcul et en robustesse.
Voyons maintenant la mise en œuvre de cette stratégie sur un cas de correction d’historique, en se basant sur la bibliothèque Python Optimal Transport : POT. Cette bibliothèque propose différentes solutions aux problèmes d’optimisation de transport relatifs aux transformations de signaux, d’images et de données pour le machine learning.
3 méthodes pour corriger les dérives dans les données historiques
L’objectif est de comparer trois méthodes pour voir si le Transport Optimal nous permettrait de corriger une dérive dans les données historiques afin d’éviter qu’elle ne biaise notre modèle. Pour ce faire nous avons pris comme exemple le cours de l’action LVMH entre 2019 et 2021, qui a chuté début 2020 durant la crise du Covid. Pour la démonstration, nous ferons l’hypothèse que cette crise a eu un effet local et non durable sur le cours de l’action, et souhaitons donc prédire la tendance future comme si la crise n’avait pas existé.
La première méthode sera naïve, nous entraînerons un modèle sans modifier aucune donnée. La deuxième offrira des données modifiées par transport optimal de façon classique alors que nous transporterons les incréments sur le troisième cas.
Comme dans le cas des boulangeries et des cafés, les distributions de probabilités représentent des valeurs discontinues (modélisées par des pics de Dirac). Ainsi chaque valeur de l’action (domaine Source) doit être transportée vers une valeur théorique potentielle hors pandémie (domaine Cible) de façon à minimiser la distance entre le départ et l’arrivée.
Le transport optimal va nous permettre d’estimer quelle aurait été la valeur de l’action si la crise n’avait pas existé, et ainsi d’entraîner notre modèle dans ces circonstances.
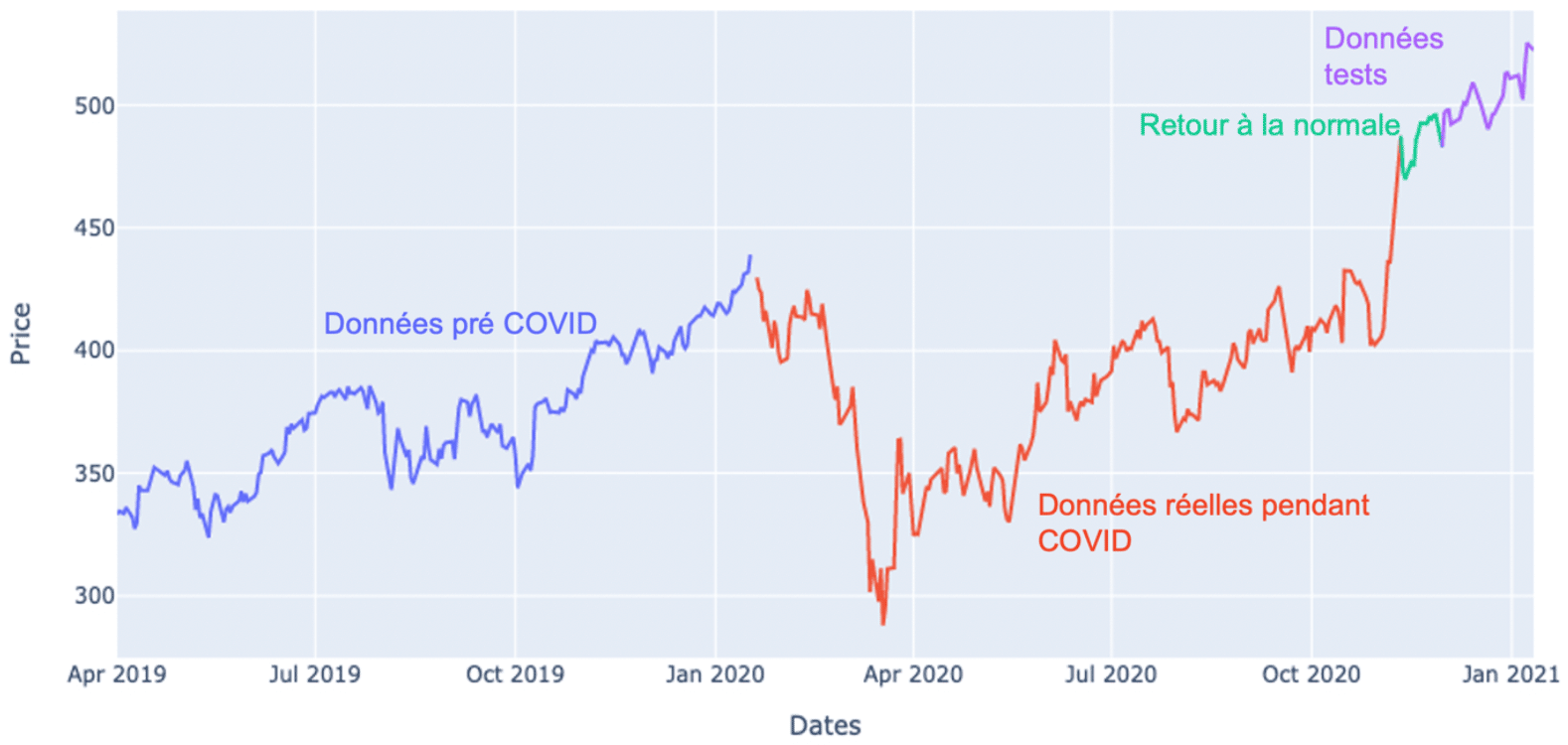
Figure 5 : évolution du prix des actions LVMH entre le 1er avril 2019 et le 21 janvier 2021
Notre jeu de données a été divisé en quatre parties – figure 5 – afin de pouvoir visualiser les différentes phases de variation dues à la pandémie.
Bibliothèque POT : Python Optimal Transport
L’outil utilisé pour notre étude est la bibliothèque open-source POT, qui offre des solutions aux problématiques faisant intervenir le Transport Optimal dans différents domaines (signal, imagerie, machine learning).
Au sein du module Adaptation de Domaine, nous avons sélectionné la méthode basée sur l’algorithme de Sinkhorn avec l’utilisation d’un paramètre de régularisation entropique. La motivation est double : d’abord cet algorithme a une meilleure complexité temporelle que la version exacte (O(n2) contre O(n3)), et le résultat est plus robuste.
Approche sans adaptation de domaine
Dans un premier temps, nous avons pris les données brutes et avons entraîné et testé un modèle Prophet. Cette première modélisation nous servira de référence pour la suite. Dans toute l’étude, nous nous attacherons au comportement qualitatif de la prédiction plutôt qu’aux scores bruts car ils ne sont pas significatifs sur un seul échantillon.
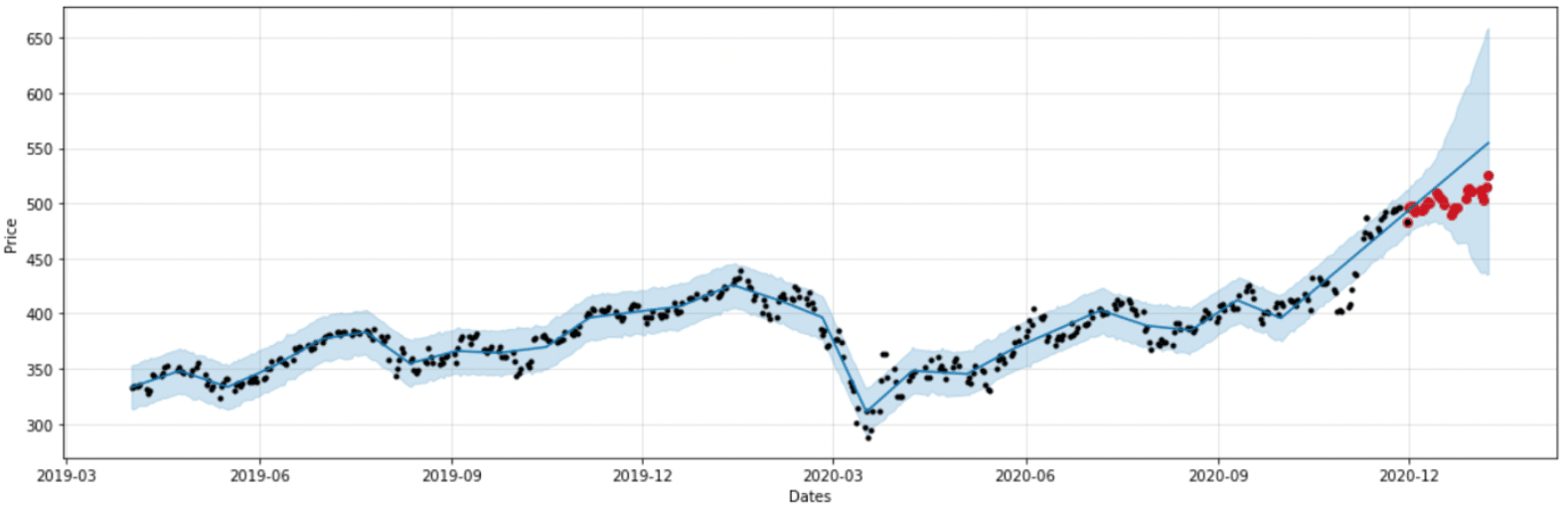
Figure 6 : modèle 1 entraîné sur les données brutes
Sur les figures 6, 7 et 8, les points noirs représentent les données réelles pour l’entraînement, les points rouges représentent les données réelles pour le test, le trait bleu représente les prédictions et la zone bleue l’intervalle de confiance.
Nous observons que le retour à la normale en fin du jeu d’entraînement perturbe le modèle dans sa prédiction, ce dernier ne rattrape pas la continuité sur le jeu de test.
Approche avec adaptation de domaine par transport optimal
Afin de gommer le « trou » induit par la pandémie sur l’année 2020, nous avons utilisé la technique du Transport Optimal afin de déplacer ces données et avoir une nouvelle distribution de données correspondant à ce que nous aurions pu observer sans la pandémie.
Cette opération met en jeu trois distributions :
- celle des données Source (historique impacté par le Covid),
- celle des données Cible (historique non impacté),
- celle des données Transportée (résultat de l’opération de transport à partir des données Source).
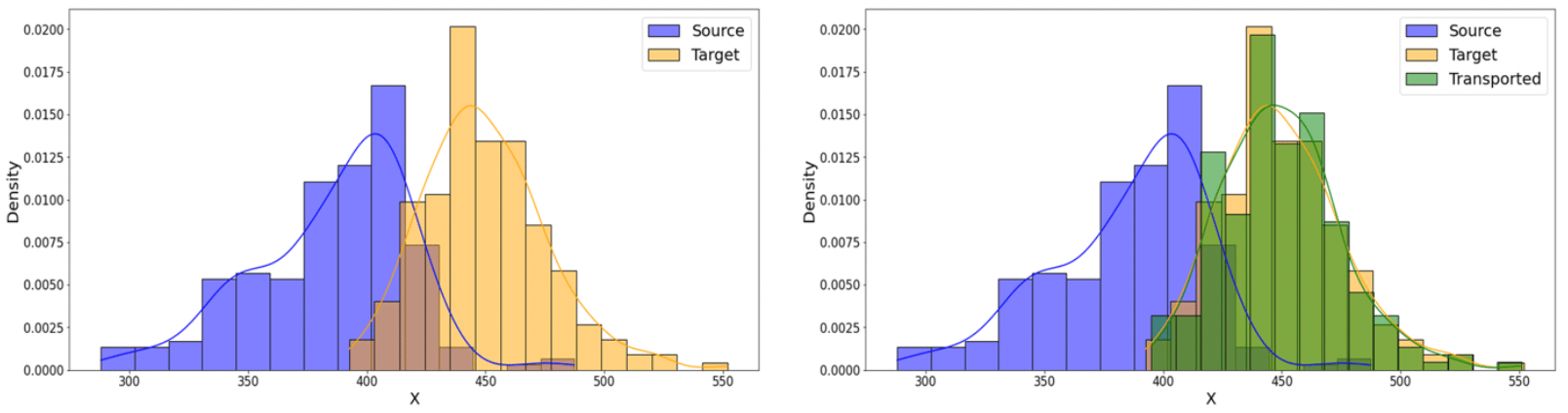
Figure 7 : création d’une distribution de données Transportée d’une distribution Source vers une distributions Cible
Ce transport a permis de déplacer nos données tout en gardant les fluctuations du marché dans les données. Sur ces nouvelles données, nous avons entraîné et testé une seconde modélisation.
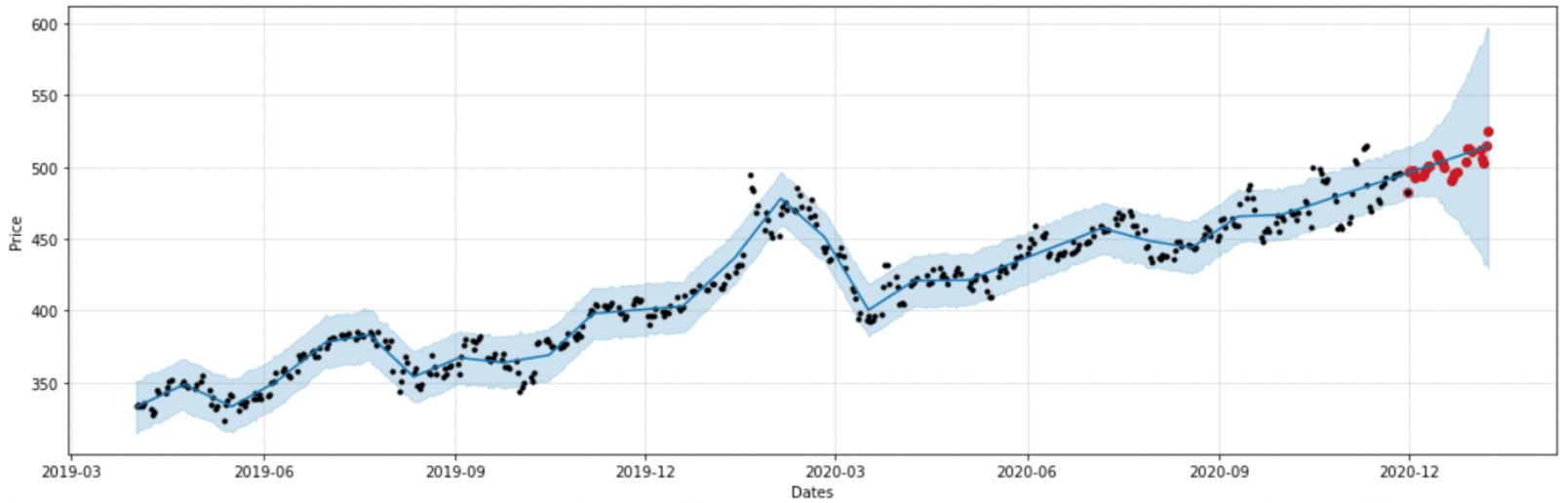
Figure 8 : modèle 2 entraîné sur des données Transportées
Transporter la distribution des données issues de la crise Covid vers une distribution de données qui aurait pu être réelle sans la pandémie offre au modèle la possibilité de sortir des prédictions dont le comportement est proche des données réelles de test. Visuellement, nous observons sur la figure 8 des prédictions plus proches de la réalité que sur la figure 6.
Cas avec transport optimal sur la série stationnarisée
Dans ce troisième cas, nous allons transformer la série temporelle afin de la rendre stationnaire, c’est-à-dire supprimer les effets de la tendance et de la saisonnalité. Plutôt que de déplacer les valeurs des actions, nous calculons les incréments entre deux journées puis nous transportons la distribution de ces incréments. Nous observons les résultats sur la figure 9.
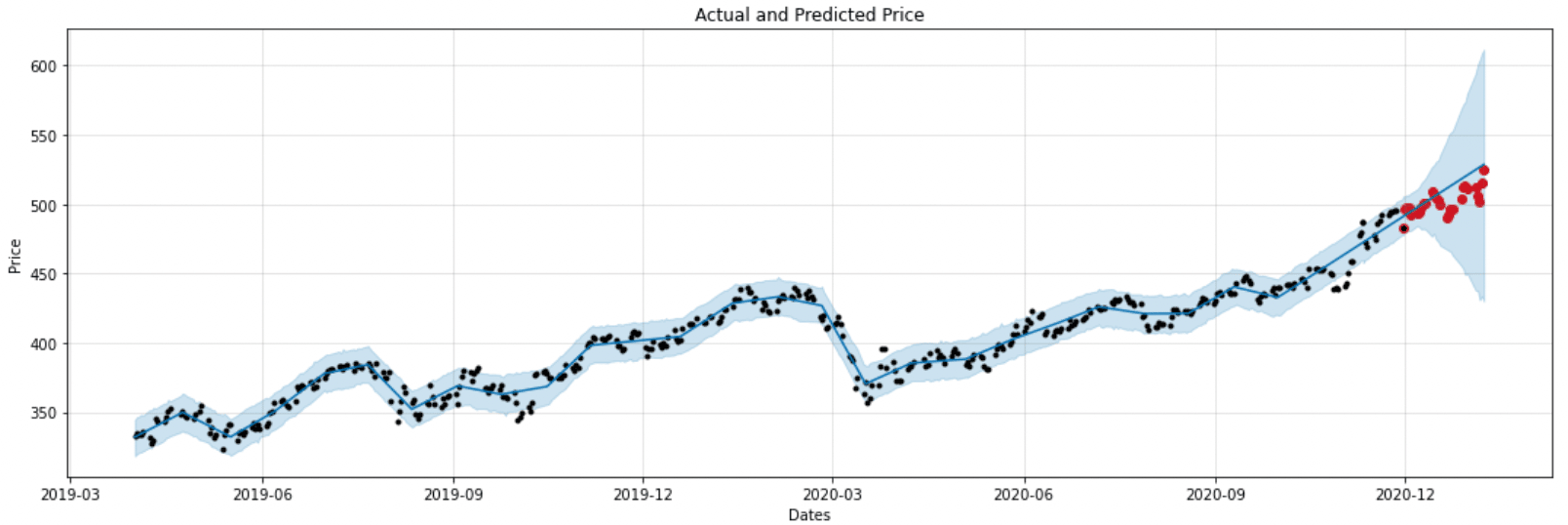
Figure 9 : modèle 3 entraîné sur les incréments transportés
La méthode parvient à capter la tendance sur la période finale, tout en étant plus robuste aux tendances. Afin d’améliorer les prédictions, nous pourrions ajouter des transformations aux données (indiquer clairement au modèle Prophet les périodes pré-Covid, Covid, post-Covid, de confinement voire les taux de saturation des hôpitaux) qui viendraient ajouter des informations utiles quant aux intervalles de données à transporter.
Conclusion
Grâce aux résultats précédents, nous pouvons conclure que le transport optimal mis en œuvre avec la bibliothèque POT permet de corriger le biais dû à la pandémie de Covid. Ce qui permet des prédictions proches de la réalité dès l’observation d’un retour à la normale sans que nous ayons eu besoin de modifier les paramètres du modèle, notamment sa réactivité aux changements de tendance. Pour pouvoir confirmer ces premiers résultats, il faudrait mettre en place un benchmark systématique sur un jeu de données plus grand et plus varié.
Les méthodes de transport offrent donc une bonne efficacité dans les résultats, mais elles sont gourmandes en temps de calcul donc difficilement utilisable pour des grands jeux de données. La bibliothèque POT propose plusieurs méthodes de transport, la figure 10 donne un aperçu du temps de calcul nécessaire à la transformation d’un échantillon suivant deux méthodes différentes . En extrapolant, la méthode EMD mettrait plus de 8h à transporter une colonne de 100 000 lignes, alors que la méthode Sinkhorn mettrait environ 1h.
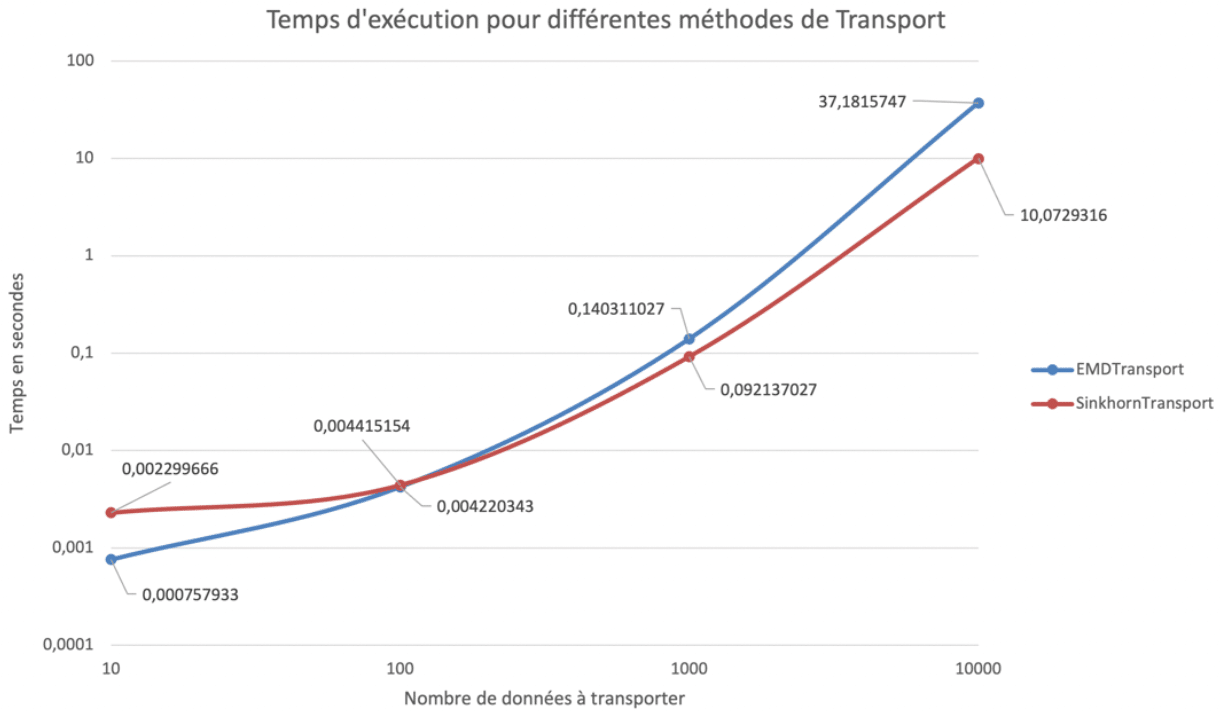
Figure 10 : temps d’exécution en secondes pour différents nombres de données transportées
Afin de compléter l’étude sur l’efficacité du transport optimal, il serait intéressant de l’appliquer dans le cas d’une dérive des données autres que temporelles, pour un modèle de classification par exemple.
Enfin nous pourrions avoir deux approches pour étudier le transport optimal :
- Transporter les données dérivées afin de les ramener dans la zone de distribution de probabilité reconnue par le modèle lors de l’entraînement.
- Transporter les anciennes distributions de probabilité vers les distributions dérivées afin de mettre à jour le modèle en refaisant un entraînement sur cette nouvelle distribution de données.
Abonnez vous à notre page Linkedin Quantmetry pour ne rien manquer de notre actualité !
Les membres de l’expertise Reliable AI développent des modèles performants, fiables et maîtrisés, sur l’ensemble du cycle de vie, pour une IA de confiance.

Data Scientist
Après plusieurs années en tant qu’Ingénieur Qualité dans l’aéronautique, je me suis orienté vers les métiers de la Data grâce auxquels je m’épanouie dans le domaine de la programmation en milieu scientifique.

Data Scientist Senior
Docteur en mathématiques appliquées à la physique statistiques, j’aborde aujourd’hui les problématiques de data science sous les angles scientifiques, techniques et métiers. J’ai un faible pour les modèles Bayésiens, les séries temporelles et l’IA de confiance !
