Tech Sprint ACPR 2021 : retour sur notre victoire

Cet article retrace notre participation au challenge Tech Sprint dédié à l’explicabilité des modèles de type « boites noires », organisé par l’ACPR (Autorité de Contrôle Prudentiel et de Résolution ). Ainsi, vous y découvrirez les idées clés qui ont permis aux gagnants (Salim Amoukou, Gauthier Le Courtois du Manoir, Philippe Neveux, Thibaud Real) de remporter ce challenge.
Objectifs et modalités du challenge
Après avoir partagé leurs réflexions sur la gouvernance et l’évaluation des algorithmes d’IA à travers un document de réflexion publié en juin 2020, l’ACPR a décidé d’organiser le 30 juin 2021 un challenge d’intelligibilité.
L’objectif était d’expliquer le fonctionnement de plusieurs modèles, accessibles sous la forme de requêtes APIs et ce, pour quatre boîtes noires. Chacune des boîtes noires provenait des banques : BPCE, Crédit Mutuel Arkéa, Société Générale et Younited Crédit, utilisait des données différentes et comportait plusieurs modèles différents. Le cas d’usage de toutes les boîtes noires était le même : expliquer un modèle de risque de crédit.
Une journée complète a été dédié à la prise de connaissance des modèles boîtes, à l’application de notre méthodologie ainsi qu’à la rédaction d’un rapport pour expliquer au jury du tech sprint notre démarche, destiné au jury du Tech Sprint. Une soutenance de 5 minutes eut lieu le lendemain pour démontrer notre méthodologie au jury.

Figure 1 : Web-app d’intelligibilité
Notre méthodologie
En mai dernier, Quantmetry publiait un Livre Blanc sur l’IA de confiance, convaincu de son importance et son impact pour l’avenir de l’IA en Europe. L’intelligibilité en est un pan entier et dépend de son destinataire. Ce fil rouge nous a permis d’établir la feuille de route suivante :
- Proposer un discours et des méthodes d’intelligibilité, pour chaque acteur concerné : client, métier, auditeur.
- Des méthodes innovantes qui font sens d’un point de vue métier et qui mettent en confiance les publics ciblés.
- Intégrer les analyses à travers une web-app, claire et facile d’utilisation.
Un discours ciblé et adapté
Notre présentation se divisait en 3 parties distinctes. Chaque partie correspondant à un type de destinataire : client, métier, ou audit. Chaque destinataire est intéressé par des éléments différents, plus ou moins techniques et précis.
Afin d’illustrer ces différences, nous avons sélectionné des clients types, aussi appelés prototypes, qui sont représentatifs d’une partie des observations.
Nous avons ainsi exposé les résultats de l’étude sous la forme d’une WebApp qui contenait trois onglets différents correspondant aux différents destinataires. Une synthèse des éléments présentés est proposée dans le tableau suivant :
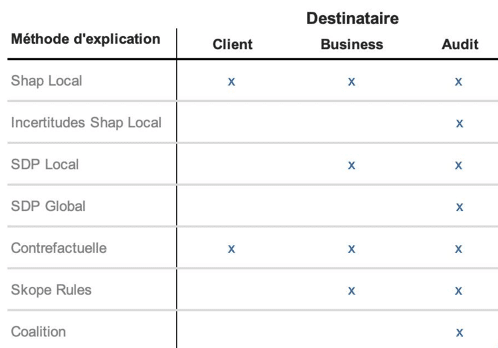
Figure 2 : Des méthodes d’intelligibilité pour chaque public
Nous déploierons très prochainement une version similaire de la WebApp produite lors du challenge.
Des méthodes d’intelligibilité innovantes et agnostiques du modèle
Devant le nombre important de modèles à expliquer, nous avons décidé d’utiliser une approche de type « modèle-agnostique ». Ainsi, les méthodes utilisées (classiques ou novatrices) pouvaient se prêter à n’importe quel modèle. Par ailleurs, nous avons également tenu à prendre en compte la singularité de certains cas, notamment en exploitant la notion de coalition de variables, comme détaillé plus loin.
Ici, vous sont présentées les méthodes innovantes que nous avons utilisées.
SHAP : oui, mais pas aveuglément
La première méthode utilisée est le calcul des valeurs de SHAP (SHapley Additive exPlanations). Nous avons ici exploité KernelSHAP qui peut être applicable à n’importe quel modèle. SHAP est basé sur la théorie des jeux. Il permet d’expliquer une prédiction liée à une observation en calculant l’influence moyenne de chaque variable sur la prédiction finale. L’étude des valeurs de SHAP sur l’ensemble des observations permet également de déterminer des notions d’importance des variables de manière globale.
Bien que SHAP soit très populaire dans le domaine de l’explicabilité, il présente néanmoins de nombreuses limites souvent méconnues (e.g. stabilité, robustesse, corrélations, attaques adversariales…). Pour cette raison, nous avons souhaité apporter plusieurs améliorations à SHAP.
La première amélioration concerne l’incertitude des valeurs de SHAP calculées. Les valeurs de SHAP sont en réalité des estimations, nous avons donc souhaité déterminer les incertitudes liées à ce calcul afin d’avoir une plus grande confiance dans les résultats affichés (https://github.com/iancovert/shapley-regression). Les incertitudes sont représentées par les barres noires du bar chart.
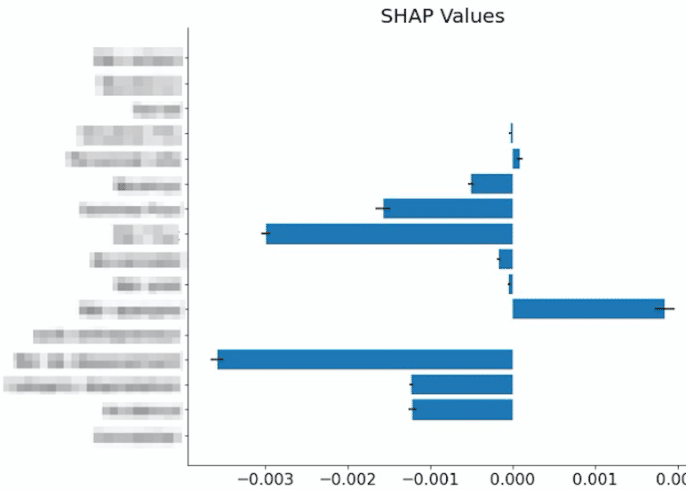
Figure 3 : Valeurs de SHAP et incertitudes correspondantes calculées sur un individu
Les SDP : Une nouvelle méthode d’explicabilité
Un autre problème concerne les valeurs calculées par SHAP qui sont presque nulles. Il est en effet très fréquent que pour une observation donnée, certaines variables n’influençant pas la prédiction se voient attribuer une valeur de SHAP proche de zéro, mais non nulle. Or, lorsqu’une personne doit effectuer un choix, elle va souvent identifier les facteurs qui lui semblent importants pour prendre sa décision, sans utiliser nécessairement toutes les variables.
Nous avons donc utilisé la notion de SDP (Same Decision Probability). Cette dernière permet d’identifier les variables qui ont eu de l’influence sur une décision donnée, pour un seuil de probabilité choisi. Ainsi on peut se restreindre à calculer les contributions des variables importantes uniquement, ces dernières étant définies comme les variables suffisantes conduisant à une prédiction donnée. Le fait de changer les valeurs des autres variables aura donc peu de chance de modifier la prédiction. On attribue alors des valeurs de SHAP nulles aux variables qui sont non importantes.

Figure 4 : SDP (Same Decision Probability) local
Dans l’exemple qui précède, nous cherchons à déterminer quelles sont les variables qui fixent la décision de l’algorithme à 90% au minimum, il s’agit des variables les plus explicatives. Pour ces exemples, si les variables bleutées sont fixées alors en modifiant les autres variables, dans 94% des cas, la décision de l’algorithme ne bougera pas. Il s’agit ici du SDP local.
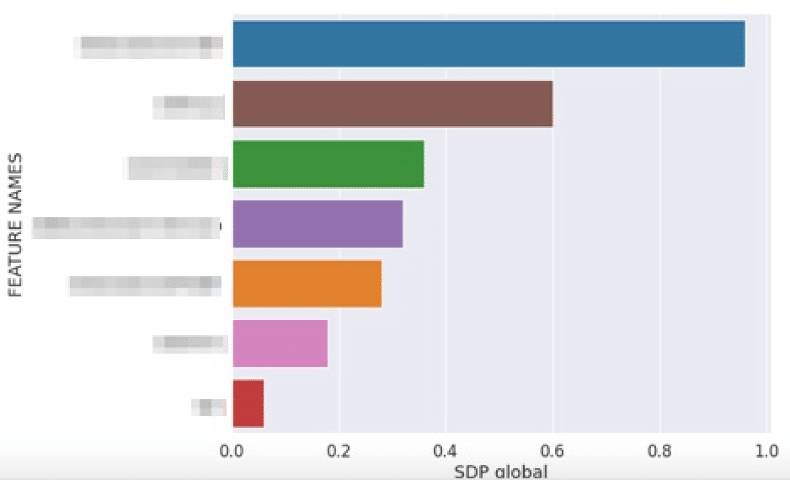
Figure 5 : SDP (Same Decision Probability) global
Nous pouvons étendre cette méthode de façon globale. Très simplement, nous comptons le nombre de fois que les variables fixées ont été utilisées pour figer la prédiction. Par exemple, la variable marron a été utilisée pour fixer 60% des prédictions.
Utiliser les coalitions de variables pour une vision plus synthétique
Les résultats ont été illustrés sur la boîte noire A mais sont parfaitement transposables à n’importe quel autre modèle. Cependant, la boite noire A possédait peu de variables, comparée aux autres. Il est intéressant de noter qu’une personne peut difficilement interpréter des résultats d’explicabilité lorsque ces derniers comportent un nombre trop important de variables, l’être humain étant capable de traiter 7 plus ou moins 2 informations en même temps. C’est pourquoi nous avons exploité la notion de coalition (Shapash et ACV) afin de regrouper les variables par groupe, thème. Nous avons illustré ce point sur le modèle B qui possédait 63 variables initiales que nous avons regroupées en 16 groupements de variables qui possédaient un sens métier proche, ou liées à un thème commun.
Un TechSprint Challengeant
Nous sommes fiers d’avoir remporté le Tech Sprint exigeant de l’ACPR. Il vient confirmer notre conviction chez Quantmetry de proposer des solutions d’intelligences artificielles intelligibles en creusant toujours plus loin la recherche. La route vers une IA de confiance continue de plus belle !
Références :
[1] Active Coalitions of Variables
[4] Livre Blanc ACPR
